W metodzie Lanczosa (Ritz) rozwiązywany jest układ równań problemów wartości własnych K j - l B j = 0.
Metoda Lanczosa polega na rozwiązywaniu układu równań problemów wartości własnych Kφ - λBφ = 0. To podejście pozwala na uzyskanie poszukiwanych pierwszych ‘n’ wartości i wektorów własnych z dowolną dokładnością.
Tolerancja (żądana zbieżność) rozwiązania problemu własnego jest określana wzorem:
Wartość parametru tolerancji (tol) definiowana jest w oknie dialogowym Parametry analizy modalnej. Aby zwiększyć dokładność obliczeń, należy zmniejszyć wartość parametru tolerancji tol. Powoduje to wzrost liczby iterakcji.
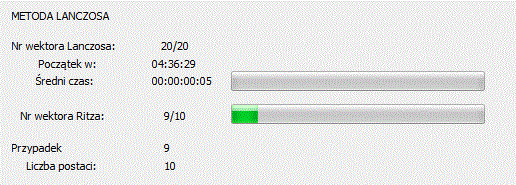
Dodatkowo podawane są następujące informacje:
- Numer wykonywanej iteracji / maksymalna liczba iteracji
- Wymagana dokładność (tolerancja)
- Dokładność bieżącej iteracji
- Liczba wymaganych postaci.
Patrz również: