Metoda blokowej iteracji podprzestrzennej służy do rozwiązywania uogólnionego problemu własnego
![]() ( 1 )
( 1 )
z którym spotykamy się w trakcie modalnej lub wyboczeniowej analizy konstrukcji. W powyższym wzorze przyjęto następujące oznaczenia:
K - macierz sztywności
B = M - macierz mas w przypadku analizy dynamicznej, w pozostałych przypadkach B = Ks
gdzie Ks jest macierzą sztywności naprężeniowej (stress-stiffness matrix) spowodowaną linearyzacją odpowiedniego operatora nieliniowego w przypadku analizy wyboczeniowej
λ - wartość własna
Φ - wektor własny.
Metoda blokowej iteracji podprzestrzennej jest zalecana w przypadkach, gdy dla konstrukcji należy uzyskać znaczną liczbę par własnych (wartości i wektorów własnych) - zazwyczaj więcej niż 10.
Jeżeli metoda blokowej iteracji podprzestrzennej używana jest w programie, to można używać wszystkie typy macierzy mas (rozłożona, skupiona z rotacjami, skupiona bez rotacji). Zakres stosowania tej metody jest ograniczony do trybu modalnego. Jeżeli wybrana zostanie metoda Lanczosa, dostępne są dwa pozostałe tryby rozwiązywania zadania analizy modalnej: pseudomodalny i sejsmiczny).
Jeżeli włączona jest opcja Weryfikacja Sturma, to podczas obliczeń przeprowadzona zostanie weryfikacja Sturma, aby wyznaczone zostały pominięte wartości własne.
Jeżeli ta opcja będzie wyłączona, weryfikacja Sturma nie będzie przeprowadzona. Metoda blokowej iteracji podprzestrzennej polega na jednoczesnych iteracjach wektora w podprzestrzeni o ustalonym wymiarze (rozmiarze). Każdy wektor, dla którego został zakończony proces zbieżności, jest usuwany z podprzestrzeni pracy, a następnie nowy wektor startowy jest dodawany zamiast niego. Ortogonalność tych wektorów jest zapewniana na każdym kroku iteracyjnym. Stosowane jest następujące kryterium zbieżności:
![]() ( 2 )
( 2 )
gdzie:
i, k - odpowiednio numer postaci i numer kroku iteracyjnego
tol - tolerancja, która jest definiowana w polu edycyjnym Tolerancja.
Należy zwrócić uwagę na fakt, że wyniki analizy modalnej i wyboczeniowej są wyznaczane z pewną dokładnością, która jest określona wzorem:
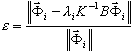 ( 3 )
( 3 )
Gdy mamy do czynienia z powolnym procesem zbieżności, zaleca się zastosowanie procedury przesunięć w analizie modalnej:
![]() ( 4 )
( 4 )
gdzie:
Kσ = K - σ M,
σ - wartość przesunięcia.
Kliknij przycisk Definiuj parametry, aby zdefiniować parametry procedury przesunięć. Jeśli opcja Aktywne przesunięcia jest wyłączona, procedura zostanie uaktywniona. Jeżeli włączona jest opcja Przesunięcia aktywne, procedura zostanie włączona; parametrem tej procedury jest liczba iteracji pomiędzy dwoma następnymi przesunięciami.
Naciśnięcie przycisku Ustaw domyślne powoduje przyjęcie domyślnej wartości liczby iteracji. Jeżeli metoda z użyciem przesunięć nie ma być używana, należy wyłączyć opcję Przesunięcia aktywne i nacisnąć klawisz OK.
Procedura przesunięć nie powinna być stosowana do analizy zadań wyboczeniowych, gdyż istnieje niebezpieczeństwo przesunięć widm wartości własnych w kierunku ujemnego obciążenia krytycznego (a co za tym idzie pominięcia dodatnich obciążeń krytycznych), jeżeli oczywiście występują dla konstrukcji ujemne wartości własne.
Aby wybrać metodę blokowej iteracji podprzestrzennej dla analizy wyboczeniowej konstrukcji, należy nacisnąć klawisz Zmień typ analizy w oknie dialogowym Typ analizy (dla wybranego przypadku obciążenia) i wybrać opcję Wyboczenie w oknie dialogowym Zmiana typu analizy. Po naciśnięciu klawisza OK na ekranie pojawia się okno dialogowe Parametry analizy wyboczeniowej pokazane poniżej. W tym oknie dialogowym możliwy jest wybór metody blokowej iteracji podprzestrzennej.
Określone pary własne są sortowane w następujący sposób | λ1 |≤ | λ 2 |≤ ... ≤ | λ n |, co powoduje umiejscowienie minimalnych parametrów obciążenia krytycznego w górnej części tabeli z wynikami.
Patrz również:
Blokowa iteracja podprzestrzenna - wykorzystanie przesunięcia