Метод блочной итерации подпространства

Метод блочной итерации подпространства используется для решения обобщенной собственной задачи

( 1 )

К этой задаче сводится модальный расчет конструкции и анализ устойчивости конструкции. Представленное выше уравнение включает символы, обозначающие следующее:

K - матрица жесткости конструкции

B = M - матрица массы в случае динамического анализа; в остальных случаях B = Ks

Ks - матрица напряжения-жесткости, создаваемая линеаризацией соответствующего нелинейного оператора при решении задачи устойчивости.

λ - собственное значение

Φ - собственный вектор.

Метод блочной итерации подпространства рекомендован в случаях, когда нужно получить большое число собственных пар (собственных значений и собственных векторов) конструкции – обычно более 10.

Прим.: Метод блочной итерации подпространства может быть применен к раздельным конструкциям.

Если используется метод блочной итерации подпространства, то можно работать со всеми типами матриц масс (согласованная, сосредоточенная с вращением, сосредоточенная без вращения). Диапазон приложений метода ограничен модальным анализом. Использование метода Ланцоша позволяет также выполнить псевдомодальный и сейсмический расчет.

Если активна опция Проверка Штурма, то во время процесса проверки будет выполнена проверка Штурма, позволяющая обнаружить пропущенные собственные значения.

Если опция выключена, проверка Штурма выполняться не будет. Метод блочной итерации подпространства состоит в синхронных итерациях вектора в подпространстве заданного измерения. Каждый вектор, для которого завершен процесс сходимости итераций, удаляется из рабочего подпространства и на его место добавляется новый начальный вектор. Ортогональность векторов обеспечивается на каждом шаге итераций. Применяется следующий критерий сходимости:

( 2 )

где

i, k - число форм и число шагов итерации, соответственно

tol - допуск, заданный в поле Допуск .

Нужно учитывать, что результаты модального анализа и анализа устойчивости, определяются с заданной точностью, описываемой следующей формулой:

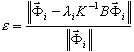( 3 )

Если процесс сходимости медленный, рекомендуется применить процедуру сдвига:

( 4 )

где

K_σ = K - σ M,

σ - значение сдвига.

Параметры процедуры сдвига могут быть заданы в диалоговом окне Определение сдвигов. Если опция Активные сдвиги выключена, процедура будет активизирована. Число итераций между двумя последовательными сдвигами рассматривается как параметр этой процедуры.

При нажатии кнопки Установки по умолчанию принимается значение по умолчанию для числа итераций. Если используется метод со сдвигом, нужно выключить опцию Активный сдвиг и нажать кнопку ОК.

Прим.: Нужно избегать установки слишком малого числа итераций между последовательными сдвигами. Это может привести частому скоплению арматуры и к декомпозиции "сдвинутой" матрицы жесткости K_σ. Это операции, требующие большой затраты времени, особенно в случае больших конструкций

Процедура сдвига не должна применяться при решении задачи устойчивости конструкции. В этой задаче существует опасность сдвига спектра собственных значений в направлении отрицательной критической нагрузки, что может привести к неучтенным положительным критическим нагрузкам, если, конечно, для данной конструкции имеются отрицательные собственные значения.

Чтобы выбрать метод блочной итерации подпространства для расчета потери устойчивости конструкции, нужно в диалоговом окне Тип расчета нажать кнопку Изменить тип расчета и в диалоговом окне Изменение типа расчета выбрать опцию Потеря устойчивости. При нажатии кнопки ОК на экране появляется диалоговое окно Параметры, в котором назначаются параметры расчета потери устойчивости.

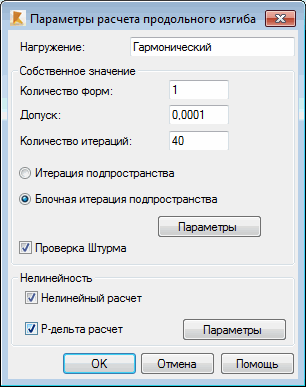
Определенные собственные пары сортируются следующим образом | λ1 | ≤ | λ 2 | ≤ ... ≤ | λ n , что приводит к тому, что минимальные параметры критической нагрузки располагаются в верхней части таблицы результатов.

См. также:

Блочная итерация подпространства – применение двига