疲劳安全系数

疲劳安全系数 (FSF) 计算基于感知的部件“无限寿命”。若要在 N 次循环之后实现感知的“无限寿命”，可构建一幅图显示平均应力和交替应力的值，从而实现 N 次循环（或无限寿命）。您可以实验性地生成这些图。但是，对于疲劳分析，您可以根据单调材料属性（例如，极限强度、屈服强度和疲劳强度）大致估算出这些图。

疲劳向导允许定义两种不同的 FSF 图，分别是：

• Goodman 图。
• Haigh 图（更通用）。

默认情况下，FSF 使用标准“Goodman”图计算，如图所示。

Goodman 图

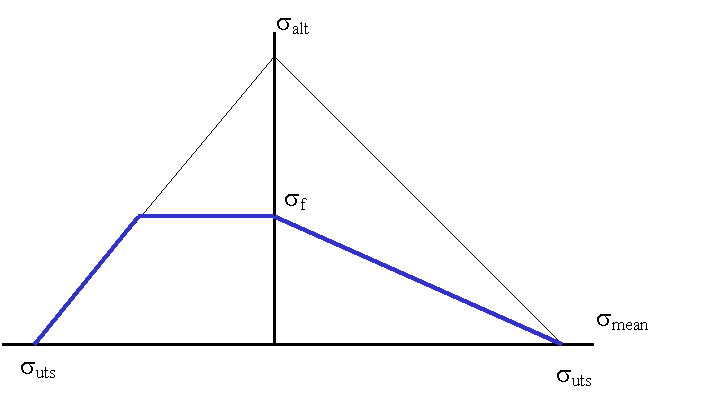
通用“Haigh”图

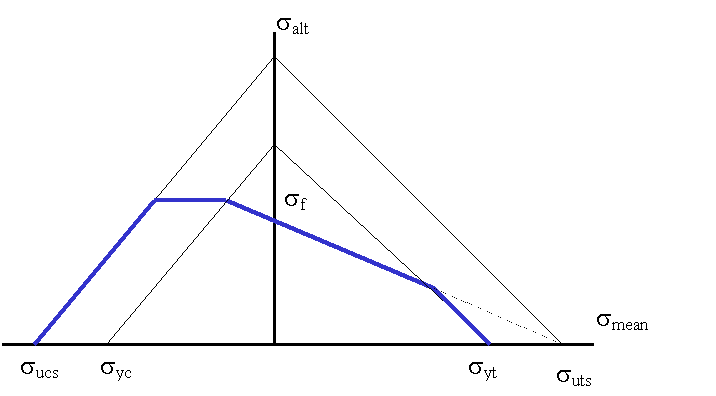
通用“Haigh”图使用六个点构建。这些点根据输入的材料 UTS（拉伸和压缩）、材料屈服（拉伸和压缩）以及材料疲劳耐久极限计算。然后，“Haigh”图上的关键点将如上图所示定义。

注： 压缩和拉伸的极限强度和屈服强度值不一定完全相同。此注释适用于铸铁等具有更高压缩强度值的材料。

FSF 计算

疲劳安全系数 (FSF) 计算基于代表相关应力循环的点（平均和交替）与“无限寿命”线的交点的比值。

疲劳向导会计算与无限寿命线相交的两种标准方法，一种是等应力比方法 (constR)，另一种是等平均应力方法 (constM)。

等应力比方法 (constR)

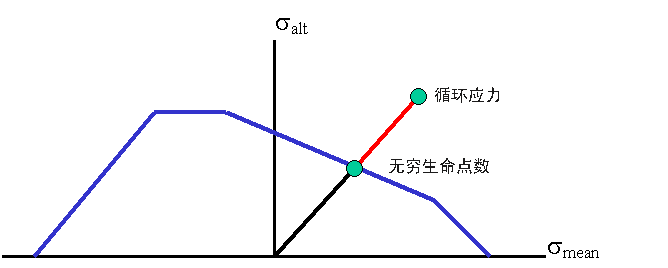
等应力比计算方法的基础是以下假设：将循环中的应力缩放到“无限寿命”线时，平均和交替应力均使用相同比值进行缩放。

等平均应力方法 (constM)

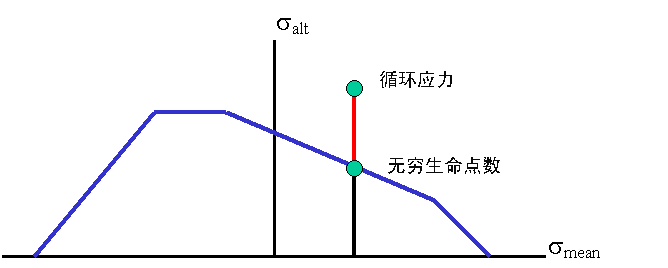
FSF 的等平均应力计算方法的基础是以下假设：在循环中将应力缩放到“无限寿命”线时，仅缩放交替应力。

相对于“无限寿命”，FSF 计算将指定一个安全系数。在计算此安全系数时，将假设构成循环的应力历史没有损伤汇总（与“寿命”计算的情况相同）。为所有循环单独计算 FSF，并报告最差的安全系数。此报告假设，如果材料/部件在最差循环中仍可实现无限寿命，则应力历史中的任何后续循环都不会产生进一步影响。这一假设对具有独特耐久极限的铁质材料是合理的。但是，对不具有该现象的材料应用同一假设时应小心谨慎。