理论概述

十九世纪初期，德国工程师 Albert 最早完成了关于疲劳的调查研究。当时人们已经认识到，材料反复经受载荷后，最终会失效。但是，随着看上去毫无故障的铁路客车轴在投入使用数英里后普遍失效，这个问题开始引起了人们的注意。后来，人们将这种现象称为疲劳。

大多数工程部件或结构都会承受某种形式的循环载荷。此类部件失效通常是在开始时仅萌生细小的裂纹，最终会形成大的裂纹和灾难性失效。裂纹萌生开始时所承受的应力级别远低于材料的单调屈服应力。随着时间的推移，“重复性的”损伤不断累积，直到最终失效。现在，人们普遍认为，超过 90% 结构性失效都源于疲劳损伤。

目前有两种基本方法可用于评估材料或部件可以承受的循环载荷的重复次数。

早期的方法利用由 Wholer 在十九世纪首次整理的材料数据。这种方法将部件中的应力与经验曲线（称为 S-N 曲线或 Wholer 线）相关联，以获取疲劳失效前循环次数的估计值。此方法至今仍在沿用，一般被称为应力-寿命方法。此方法利用部件应力，并假定应力位于材料的弹性区域内。因此，此方法最适合需要 100000 次以上循环才会失效的疲劳失效。

第二种更为现代的方法利用材料应变来预测失效。描述应变与循环的关系的曲线可根据测试或经验公式（这与应力-寿命方法类似）得出。使用这种方法的主要优点在于，应变-寿命曲线代表部件的局部应变状态，可以解释局部塑性变形。这大大提高了在发生局部屈服的载荷级别预测寿命的准确性。

疲劳向导同时使用这两种方法来预测疲劳寿命。

载荷的定义

疲劳损伤是由于在结构上施加一段时间重复载荷造成的。若要分析疲劳失效，必须定义施加的载荷。在疲劳向导中，您可以定义两种基本载荷类型，其中最简单的形式是恒幅谐波。

通过定义应力振幅 sa 和平均应力 sm 可以全面描述该载荷。重复循环是一个谐波周期，即图 1 中的点 1-2-3-4。

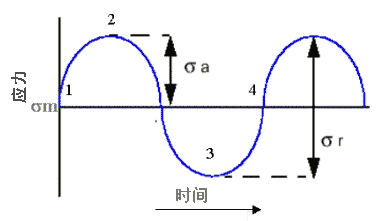
图 1 恒幅谐波载荷

第二种载荷类型是变幅载荷，这种类型更常见。

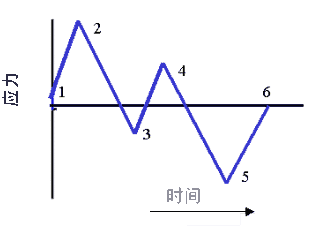
图 2 变幅载荷

变幅载荷由多个单独的恒幅循环组成。这些单独的循环每个都可以具有不同的振幅和均值，并且可以叠加起来或依次排列起来。图 2 显示了一个简单的变幅载荷示例。您可以看到，图中有两个简单的循环：1-2-5-6 构成一个大振幅循环，其上叠加一个小循环 3-4-3。因此，变幅载荷可以分解成多个更简单的恒幅载荷。然后，在疲劳分析中使用它们来预测损伤。

如果将变幅载荷用于疲劳计算，则必须应用一种方法来提取“子循环”。疲劳向导采用的是标准雨流计数算法。

雨流计数和疲劳损伤

使用应力-寿命和应变-寿命方法预测疲劳失效依靠的都是单循环损伤曲线。此损伤曲线将重复次数与一个简单循环的应力或应变幅值关联在一起。如果结构载荷是简单的恒幅类型，则可以直接使用此曲线。但是，如果定义的是变幅载荷，则需要执行几个步骤来针对施加的载荷计算寿命。

首先，选取峰-谷作为载荷历史。此过程会扫描时间历史，找到非“反向”点的任意点并将其丢弃，从而减少不必要的数据。接下来，通过标准的雨流计数算法来处理缩减后的时间历史，这一过程可提取一个个单独的循环。然后，将这些单循环与单循环损伤曲线结合使用，以便计算每个循环的寿命。

计算时间历史内每个单循环的寿命后，需要使用一种方法来确定累积损伤或总寿命。疲劳向导利用得到普遍认可的“Miner 法则”。此法则规定载荷历史内累积的总损伤是各个循环损伤的线性和。

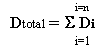
或

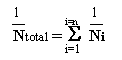
其中 N 代表寿命（以重复次数表示），D 代表损伤。

应力寿命方法

应力寿命方法利用称为 SN 曲线的单循环损伤曲线。此曲线将应力幅值与疲劳失效前的循环次数相关联。由于此方法已广泛应用多年，因此，此类曲线以及与此类曲线相关的材料数据很容易就能得到。与曲线一起使用的应力值取决于曲线中所表示的数据，在一定程度上还取决于工程师的判断。疲劳向导的单轴版本在其计算中使用“最差绝对主应力”，因为应力的方向假定为恒定不变。

疲劳向导根据工程师输入的材料数据从内部生成 SN 曲线。所需的数据是材料的单调拉伸强度以及“耐久极限”。

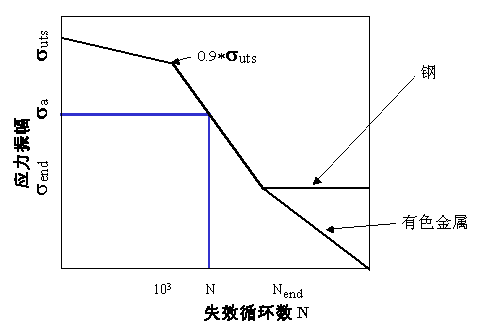
图 3 SN 曲线

SN 曲线采用图 3 中所示的形式。SN 曲线始终在双对数比例上绘制，如图所示。此曲线从 log(N)=1 时的单调拉伸强度 suts 开始。然后，常见的做法是通过一条值达到 90% suts 的直线，近似估计 1000 次循环的值。SN 曲线的主坡度从 1000 次循环点处延伸到与“耐久极限”对应的寿命值以及与 send 等效的应力幅值。之后，超出耐久极限的行为将取决于材料是铁合金还是非铁合金。通常，对于钢而言，将显示真实的耐久极限和扁平的 SN 曲线。相反，铝合金和其他非铁合金在高循环处显示的 SN 曲线要陡峭些。疲劳向导允许用户区分这两种情况。

平均应力效应

您通常需要为全反向测试提供 SN 曲线。这表示在相等的拉伸和压缩状态之间施加应力的循环。在现实的结构载荷中，循环载荷围绕非零均值状态振荡更为常见。此非零均值状态对失效前寿命具有重要影响。当使用标准 SN 数据时，需要一种方法来考虑循环中存在的平均应力。

疲劳向导允许使用“无平均”、“Gerber”和“Goodman”修正计算疲劳寿命。

应力集中

通常，FE 分析可明确建模，并计算局部集中区域中的应力，因此不可能需要缩放额定应力。但是，如果需要对已计算的 FE 应力执行任何线性缩放，疲劳向导将提供一个常规缩放系数 Kt。

s_e = K_t.s_额定

其中，s_e = 缩放的弹性应力

耐久极限修改器

SN 曲线数据通常是从对标准尺寸抛光样品执行的测试中获得的。将这些“实验室”测试数据应用于真实的工程部件有时需要进行修正。修正通常采用的形式是将“修正器”应用于样品的耐久极限。

应用修正器时可以考虑尺寸、表面强化、应力梯度、表面处理、载荷类型等因素。这些修正器在很多工程教科书中都有详尽记录，如果需要，工程师可以很轻松地得到。

s_最终修正 = s_最终 . n_尺寸 .n_表面 …

其中 n 代表相应的修正器

疲劳向导提供了适用于表面强化效果和统计效果的标准修正器，还提供了通用修正器以输入计算的合并值。修改 SN 曲线时，疲劳向导会按照如上所述缩放样品的耐久极限，并围绕 1000 次循环点旋转 SN 曲线。

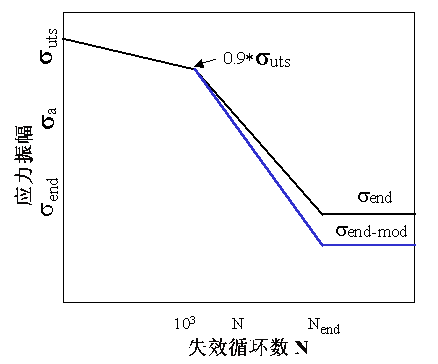
图 4

应变寿命方法

应变寿命方法产生于上世纪六十年代，它是对应力-寿命方法的一种改进，用于预测承受塑性变形的材料的疲劳失效。因为该方法针对循环载荷测量或计算应变幅值（而不是应力），并将其与描述应变幅值与寿命的经验图进行比较，所以原理与上述方法是相同的。相比于应力-寿命方法而言，该方法的优势在于测试数据中没有关于完全弹性变形的内在假定。

应变-寿命曲线

应变-寿命曲线描述实验室测试的样品的疲劳行为。样品通常在全反向应变控制的载荷下进行测试，并与寿命和裂纹萌生相关联，而且会绘制一条经验曲线，描述应变幅值与失效循环次数的关系。

对于变形为完全弹性的较低级别的应变，疲劳行为与应力幅值关联，并且

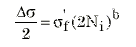
其中 s_f’ 是疲劳强度系数，b 是疲劳强度指数，两者均是从应力幅值和寿命的双对数拟合中提取的。

对于变形主要是塑性变形的较高级别的应变，疲劳行为能与应变幅值建立最佳关联，因此公式为：

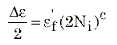
其中 e_f’ 是疲劳延性系数，c 是疲劳延性指数，两者均是从塑料应变幅值和寿命的双对数拟合中提取的。

常规应变寿命曲线或 Coffin-Manson 曲线然后将描述为这两条单独的直线曲线的组合，因此公式为：

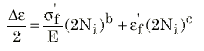
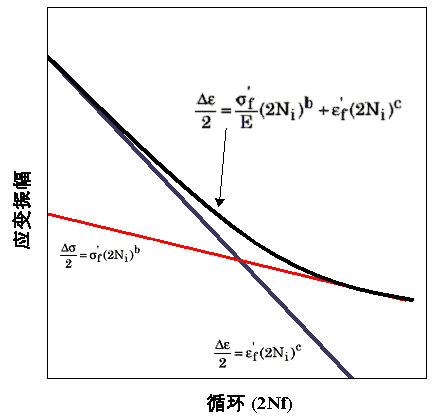
图 5 恒幅应变寿命曲线。Coffin-Manson 关系。

近似估计不可用的各种应变-寿命系数

您可以使用多种方法根据更容易获得的单调数据（例如拉伸强度、模量等）来近似估计基于应变的材料数据。疲劳向导使用的方法即是 Seeger/Beste 使用的方法。在许多介绍基于应变的疲劳计算的教科书中都可以找到此方法。此方法使用以下公式来近似估计应变寿命曲线（基于应变的系数）：

钢：

• K' = 1.65 * UTS
• n' = 0.15
• Sf = 1.5 * UTS
• b= -0.087
• c= -0.58
• Ef = 0.59（如果 UTS/E < 0.003）
• Ef = 0.59*(1.375-125*UTS/E)

其他：

• K' = 1.61 * UTS
• n' = 0.11
• Sf = 1.67 * UTS
• b= -0.095
• c= -0.69
• Ef = 0.535

平均应力修正

前面介绍的恒幅寿命曲线是通过在全反向载荷（即使用零均值偏移）下进行材料测试生成的。在现实的工程载荷循环中，必然存在非零均值应变。

为了对应变循环中存在的非零均值进行修正，疲劳向导使用两种方法来修正简单应变寿命曲线，即 Morrow 修正和 Smith-Watson-Topper 修正。

执行 Morrow 修正的应变-寿命曲线

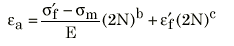
执行 SWT 修正的应变-寿命曲线

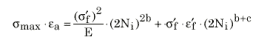
弹塑性材料数据

由于应变-寿命数据是从承受超出弹性极限的循环载荷的材料中提取的，因此必须定义循环应力-应变材料曲线。

疲劳向导利用两种得到普遍认可的经验公式来定义循环稳定应力-应变曲线。

循环应力-应变曲线通过使用 Ramberg-Osgood 关系来构建，以确定材料常数 K' 和 n'，也就是，循环硬化系数和循环硬化指数。

Ramberg-Osgood 关系

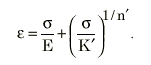
若要生成完整的循环应力-应变曲线，这里将使用 Masing 理论，因此公式为：

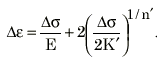
通过组合这两种关系，我们可根据两个材料常数，生成循环稳定应力-应变曲线的完整滞后回线。

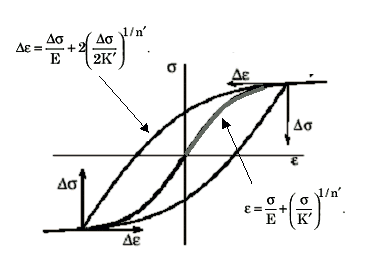
图 6 循环稳定应力-应变曲线

Neuber 修正

许多基于 FE 的疲劳规范都使用弹性 FE 分析的结果。这使您可以执行相对简单的 FE 计算，而不需要花费额外的开支和时间来运行非线性求解。如果以后要使用这些弹性应力执行基于应变的寿命计算，请采用一种方法，将基于 FE 的弹性应力转换为等效弹塑性应力（和应变）。

针对此转换有诸多建议的方法，而疲劳向导使用最常用的 Neuber 修正。

应力-寿命方法

• 从 FE 结果读取弹性应力数据。
• 提取最差绝对主应力。
• 使用 Kt 缩放弹性应力。
• 采用雨流计数方法从载荷的时间历史中提取循环次数。
• 根据耐久极限修正器修改 SN 曲线。
• 使用平均应力修正计算循环的损伤。
• 根据 Miner 线性法则对损伤求和。
• 输出所有节点的疲劳寿命或安全系数。

应变-寿命方法

• 从 FE 结果读取弹性应力数据。
• 提取最差绝对主应力。
• 使用 Kt 缩放弹性应力。
• 对局部应力执行 Neuber 修正。
• 使用循环稳定应力/应变曲线构建完整的局部应力/应变时间历史。
• 在时间历史中提取所有闭合滞后回线。
• 根据材料数据构建单循环应变-寿命曲线。
• 根据耐久极限修正器修改应变-寿命曲线。
• 使用平均应力修正计算循环的损伤。
• 根据 Miner 线性法则对损伤求和。
• 输出所有节点的疲劳寿命或安全系数。