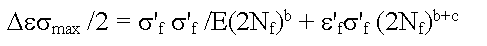循环应力和应变
反复承受恒幅应变的材料最终会形成一个重复的稳定应力/应变滞后回线。您可以在相同的轴上绘制以不同应变幅值创建的几条滞后回线。之后,如果通过所有滞后回线的顶点绘制一条曲线,即生成“循环应力-应变”曲线。这条人工曲线的目的在于呈现材料的稳定行为(经过初始循环软化或硬化后)。
循环应力-应变曲线定义为:
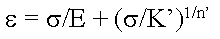
其中
K' = 循环应变硬化系数
n' = 循环应变硬化指数
基于局部应变的疲劳与寿命的关系
您可以在固定应变极限之间循环测试一个平滑测试样品,直到它出现裂纹。如果在不同弹性应变极限之间循环测试若干此类样品,则可以得到裂纹萌生前的循环次数与弹性应变幅值的关系。如果在双对数轴上绘制它们,则这些点会近似形成一条直线。Basquin 首先提出了这种关系。
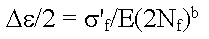
后来,Manson 和 Coffin 提出,在塑性应变幅值与疲劳失效前循环次数之间也存在类似的关系。
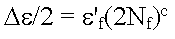
因此,总应变-寿命关系可以定义为:
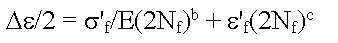
其中

疲劳向导中提供了两种方法来定义这些基于应变的材料常数。
高级
这些参数将直接输入到疲劳向导,以定义基于应变的疲劳寿命关系。
近似
疲劳向导根据输入的材料拉伸强度和材料类型(钢或其他)近似估计参数值。Seeger 方法用于计算适当的材料常数,有关详细信息可在标准教科书中找到。此方法是一种近似法。它只有在缺少实际测试数据时才使用。
Seeger 方法使用以下公式近似绘制应变-寿命曲线(基于应变的系数):
钢:
- K' = 1.65 * UTS
- n' = 0.15
- Sf = 1.5 * UTS
- b= -0.087
- c= -0.58
- Ef = 0.59(如果 UTS/E < 0.003)
- Ef = 0.59*(1.375-125*UTS/E)
其他:
- K' = 1.61 * UTS
- n' = 0.11
- Sf = 1.67 * UTS
- b= -0.095
- c= -0.69
- Ef = 0.535
平均应力修正
针对基于局部应变的疲劳与寿命的关系,人们提出了几种方法来考虑循环中平均应力的影响。疲劳向导使用以下两种方法:Morrow 修正和 Smith-Watson-Topper 修正。
Morrow 修正
应变-寿命关系中的弹性部分通过减去循环平均应力来修正。此修正基于寿命较长时平均应力的影响也更大这一观察。
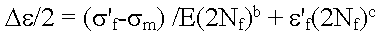
Smith-Watson-Topper 修正
Smith Watson 和 Topper 认为疲劳寿命是循环中应变幅值和最大应力的乘积的函数。该因素带来了以下形式的应变-寿命关系: