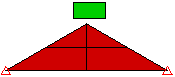
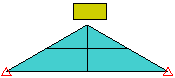
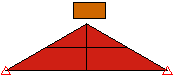
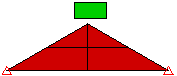
由于不存在一组可为所有模型提供精确解的接触参数值,因此用户必须准确了解每个参数的功能,才能为给定问题确定一组合适的值。
用户可以分别为每个接触对自定义接触参数。在树视图中选择接触对,单击鼠标右键,然后选择“设置”。或在“MES:面面接触”主对话框(电子表格)中,单击该接触对的“参数”列。两种方法都可访问“接触对的控制和参数”对话框。(如果接触对的参数发生更改,则“参数”列中将显示“自定义”。否则,“参数”列将显示“默认”。)
“接触对的控制和参数”对话框
接触问题类型
在“接触问题类型”下拉框中,选择可能在分析中随时出现的通用接触类型。此选择可控制自动接触刚度计算的行为。在某些情况下,选项显而易见。在其他情况下,可能不清楚接触是低速还是高速。区别是求解效率不同。任一选择都应提供精确的结果。可用的选项如下所示:
- 低速接触(挤入式):接触对之间的接触特点是两个部件缓慢接触(低速)或部件持续进行接触(挤入)。可以使用自适应接触刚度程序,但默认不使用。
- 高速接触(碰撞):接触对之间的接触特点是发生高速变化,例如碰撞或坠落测试。默认不使用自适应接触刚度程序。
接触方法
在“接触方法”下拉框中,选择将用于所选接触对的接触方法。选项如下所示:
- 无摩擦接触:此接触方法允许部件相互之间沿接触表面进行较大的相对运动。部件在整个事件期间能够开始和结束接触。没有任何摩擦阻止表面之间的运动。这是最常见的接触方法。
- 摩擦接触:此接触方法与无摩擦接触相同,但可以定义摩擦力来阻止表面之间的滑动。必须定义的系数取决于“为摩擦建模”部分中指定的“摩擦定律”设置。
- 无摩擦滑动/无回弹接触:此接触方法允许两个表面在接触前自由移动,接触后节点将不会分离,即使在张力作用下也是如此。可以单独约束切向方向。使用“滑动/无回弹接触选项”部分中的“无滑动”复选框可防止部件接触时发生滑动;在这种情况下,接触零件将变成粘合状态。否则,如果“无滑动”复选框未处于激活状态,则表面可以互相滑动。请注意,如果未激活“无滑动”选项,则表面可能分离。
- 摩擦滑动/无回弹接触:此接触类型类似于上面介绍的滑动/无回弹。区别在于表面接触后将包含摩擦力。可以在“为摩擦建模”部分中定义静摩擦系数和滑动摩擦系数;有关说明,请参见上面的“摩擦接触”。 注: “滑动/无回弹接触选项”部分中的“无回弹”复选框始终处于选中状态且无法更改。仅当在“接触方法”下拉框中选择了两个“无回弹接触”选项之一时,“无回弹”限制才适用。对于其他接触方法,将忽略此复选框。
- 固联接触:此方法用于仿真包含不匹配节点的表面之间的粘合接触。如果选择此接触方法且对应表面最初位于指定距离内,则认为这些表面在事件过程中将永久粘合,不会分离或滑动,即使在张力作用下也是如此。若表面间的距离大于指定距离,则不会考虑接触情况。可以使用“固联接触选项”部分控制指定距离。如果未激活“固联接触初始干涉”复选框,则将使用表面之间的初始距离作为接触距离。如果已激活此复选框,则必须在“固联接触距离”字段中指定该距离。使用此接触方法的分析速度比表面节点匹配的分析速度慢。 注: 仅表面上节点的三个平动(Tx、Ty、Tz)连接在一起;转动不连接。因此,在从块体部件面投影出来的壳单元排列(如由壳组成的悬臂梁)中,如果仅在壳和块体之间使用固联接触,则壳部件可以在块体支架上自由转动。
接触类型
在“接触类型”下拉框中,选择将用于所选接触对的接触类型。
将接触描述为“面对面”接触有些令人误解。在实际中,是指第二个部件/表面上的节点与第一个部件/表面的表面连接,从而防止节点穿过表面。或者,反之亦然:第一个部件/表面上的节点可以连接到第二个部件/表面的表面。在任何情况下,都不会阻止一个部件的表面穿过第二个部件的表面。
“接触类型”的选项如下:
- 自动:默认方法将允许处理器根据涉及的接触表面(网格)和材料模型在“点对面”和“面对面”接触类型之间进行选择。处理器还将确定用作主接触面的表面。(处理器可以在分析开始之前切换第一个和第二个部件/表面。)但是,如果分析中出现大变形,则“自动”选项可能无法选择最佳接触类型。在这种情况下,请检查通过“自动”选项选择的设置有效性;选择的接触类型(以及每个部件中的单元数列表)会在日志文件中列出。
- 面对面:当次要部件上的节点尝试穿过主要部件的表面时,此选项指示发生接触,反之亦然。主要部件上的节点可以接触次要部件的表面。
- 点对面:当次要部件上的节点尝试穿过主要部件的表面时,此选项指示发生接触。主要部件/表面上的节点可以通过次要表面。
- 点对点:如果两个表面之间的相对滑动可忽略不计,则此方法为最佳方法。当次要部件上的节点尝试通过主要部件上的节点时,此选项指示发生接触;不检测主要部件的节点和表面之间的接触。无论部件如何移动,接触力将始终存在于连接在一起的原始节点对之间。创建“点对点”接触后,“结果”环境将显示模型中的其他部件:一个“接触”单元部件对应一个“点到点”接触对。
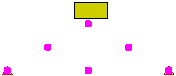
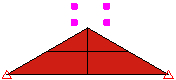
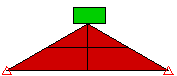
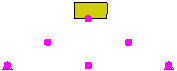
“点对面”方法速度较快,但必须意识到第一个部件上的点可能穿过第二个部件上的表面;不检测此类接触。“面面”接触可提供更好的接触检测功能,但会生成更多的接触单元。它指明目标部件/表面上的节点无法穿过主部件/表面上的节点定义的表面(与“点对面”接触相同),且主部件/表面上的节点无法穿过目标部件/表面上的表面。请参见图 2。
|
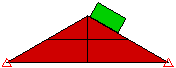
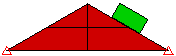
面面接触
|
点对面接触 (点在楔形体上)
|
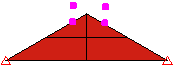
点对面接触 (点在块体上)
|
|
时间 = 0 |
||
|
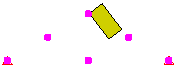
等效系统。两个部件的表面通过接触连接。 |
等效系统。仅楔形体上的节点与接触有关。 |
等效系统。仅块体上的节点与接触有关。 |
| 时间 = 0.024 秒 | ||
|
块体的表面与楔形体的表面/节点接触。 |
块体的表面与楔形体的节点接触。 |
在块体的节点与楔形体的表面接触后,才会发生接触。楔形体穿过块体。 |
| 时间 = 0.12 秒 | ||
|
块体的表面沿楔形体的表面向下滑动。 |
块体从楔形体的节点之间穿入。 |
块体卡在楔形体上。 |
| 时间 = 0.15 秒 | ||
|
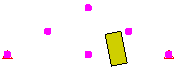
|
|
|
图 1:接触类型比较 块体落到楔形体上的三个模型。每个模型均使用不同的接触类型。 |
||
如果接触对中的表面位于壳单元的部件上,请选择接触对涉及的壳侧。(顶部是“单元定义”对话框中定义的单元法线点的相反侧。)仅当两个主体从指定的方向靠近时,才会发生接触。例如,如果指明与壳顶部发生接触,则第二个主体从顶部移动到底部时将发生接触。如果第二个主体从底部向顶部移动,则不会发生接触。另一种形象说明如下:仅当第二个对象从壳外侧靠近时,它才会与选定侧(顶部或底部)接触。如果它穿过壳到达所选侧,则不会检测到接触。请参见图 3。
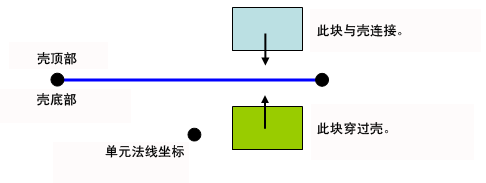
图 2:定义为与壳顶部接触的两个块体
仅当线单元上的节点与第一个部件/表面的表面进行接触时,线单元(梁、桁架)接触才能检测到接触。此外,在“进行接触的节点”下拉框中指定接触要考虑的节点是线单元上的所有节点(“线单元上的所有节点”)还是只是端节点(“仅单元末端的节点”)。例如,由梁单元组成的牙刷上的鬃毛仅需要鬃毛末端上的节点与牙齿接触;将仅使用位于单元末端的节点。但由桁架单元组成的安全网需要检测网上所有节点和跌落对象之间的接触;将使用线单元上的所有节点。
“为摩擦建模”部分
在无摩擦的接触中,单元刚度矩阵是对称矩阵。如果存在摩擦,矩阵将变成不对称矩阵。使用不对称求解器的计算成本高于使用对称求解器的成本。为了提高效率,MES 强制单元刚度对称,以便使用对称求解器求解摩擦接触。
如果在分析中考虑摩擦接触,则求解过程极易受到滑动过程的干扰和影响。接触表面开始滑动后,滑动之前的平衡状态将不再有效,处理器必须在求解过程中尝试找到新的平衡状态。此外,对称近似可能会导致收敛效果不佳。每个可用的摩擦定律选项都会尝试以不同的方式控制求解不稳定性。
有三种“摩擦定律”可用于 Simulation Mechanical 中的非线性面面接触:
- 修正的库仑摩擦
- 库仑与粘性摩擦
- Smooth Coulomb friction
在随后的子部分中将讨论每个摩擦定律及其适用的参数。
修正的库仑摩擦
此摩擦定律使用经典摩擦算法:库仑摩擦。在基础库仑摩擦模型中,两个接触表面在发生相对滑动之前,可以承受一定大小的剪切应力(由摩擦系数和法向接触压力决定)。库仑摩擦模型如下定义:τ = μ,其中 μ 是摩擦系数,P 是法向接触压力。面面接触可定义静摩擦系数 (μs) 和动摩擦系数 (μd)。理想情况下,剪切应力超过 μsP(通过“静摩擦系数”输入得出)后,两个表面将开始滑动。此外,剪切应力将变为 μdP,此时使用的是“滑动摩擦系数”值。
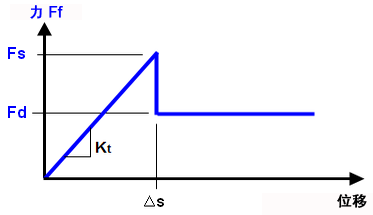
从数字上很难实现理想情况(剪切应力超过静态值之前无运动),如图 3 所述。因此,在使用此摩擦定律时需要定义“切向刚度比”。“切向刚度比”是切向接触刚度 (Kt) 与法线方向接触刚度(K,在“高级”按钮下设置。请参见页面面面接触高级控制。)之间的比值。切向刚度越大,精度越高,但所需迭代也越多。切向刚度越小,提供的收敛效果越好(运行时间越短),但可能会降低精确度。建议的值范围是 0.01 到 1,默认值为 0.01。随着静摩擦系数逐渐增大,建议使用较小的切向刚度比。
|
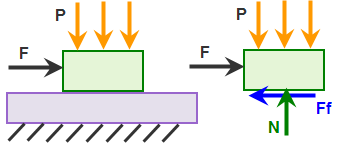
(a) 模型和顶部块体的自由体受力图。作用力 F 随时间不断增大,直到超过静摩擦力。 |
|
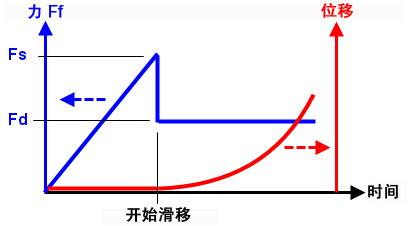
(b) 摩擦力 Ff 与时间的关系图(蓝色曲线)和位移与时间的关系图(红色曲线)。摩擦力 Ff 达到静摩擦力限值 (Fs = μs * N) 前,部件不运动。超过静摩擦力后,摩擦力 Ff 将从 Fs 下降到 Fd (= μd * N),部件开始加速。 |
|
(c) 组合 (b) 中的图形以显示摩擦力与位移的关系。理想情况下,在摩擦力达到 Fs 后才会发生位移,之后便开始滑动。从数字上来说,这种情况很难实现,因为只要存在位移即暗示摩擦力为 Fd。 |
|
(d) 为了避免 (c) 中的数值不稳定性,当摩擦力小于静态限值 (Fs) 时,允许部件出现小幅度位移 (Δs)。运动量通过切向刚度 (Kt = Fs/Δs) 控制。较小的 Kt 值允许部件在开始滑动前移动较大的位移且更易于收敛;而较大的 Kt 值(较陡的斜坡)允许部件在开始滑动前移动较小的位移且难以收敛。切向刚度的计算公式为切向刚度比 x 法线方向的刚度。 |
| 图 3:修正的库仑摩擦的切向刚度 |
库仑与粘性摩擦
与修正的库仑摩擦定律不同,库仑与粘性摩擦定律不会同时考虑静摩擦系数和动摩擦系数。在修正的库仑摩擦定律中,需要相对较大 的力来克服静摩擦并开始运动。滑动开始后,摩擦力将 降低 ,因为滑动摩擦系数小于静摩擦系数。因此,摩擦力突变将造成力的不连续性。在库仑与粘性摩擦定律中,滑动开始后不会出现摩擦力不连续。相反,随着滑动速度不断增加,摩擦力将逐渐 变大 。
必须为“库仑与粘性摩擦”选项定义两个参数:
- 滑动摩擦系数 (Fd):此项也称为动摩擦系数。它是保持相对运动所需的切向力与接触部件之间的法向力之比。例如,如果需要 15N 的切向力才能保持块体沿相邻部件滑动,且二者之间的法向接触力为 100N,则滑动摩擦系数为 15N / 100N = 0.15。对于此摩擦定律,应根据速度相对较低的滑动计算滑动摩擦系数。
- 粘性摩擦系数 (νf):这是摩擦力斜率与滑动速度的关系曲线。克服粘滞效应所需的力与速度成比例,这适用于所有粘滞效应。
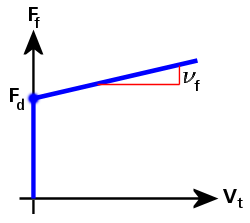
图 4:摩擦力与滑动速度的关系(库仑与粘性摩擦)
在图 4 中,摩擦力 (Ff) 曲线如下定义:
Ff = Fd + νf Vt
其中
Fd 为动(滑动)摩擦力,
νf 为粘性摩擦系数,
Vt 是两个部件之间的切向(滑动)速度。
如果 νf = 0,则 Ff = Fd
Smooth Coulomb friction
与“库仑与粘性摩擦”定律一样,“Smooth Coulomb friction”定律仅考虑滑动摩擦系数。这消除了使用“修正的库仑摩擦”定律时静态和滑动条件之间出现的摩擦力不连续性。静态和滑动条件之间的过渡将因包含平滑过渡因子 (Φ) 得到进一步稳定。
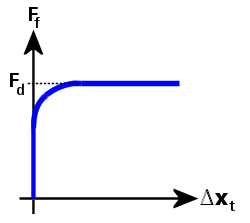
图 5:摩擦力与切向相对位移的关系 (Smooth Coulomb friction)
在图 5 中,摩擦力 (Ff) 曲线如下定义:
Ff = Fd Φ,
Φ = tanh(3 Δxt / δ)
其中
Fd 为动(滑动)摩擦力。
Φ 是过渡因子,它可使得摩擦力随着切向相对位移逐渐接近零而平滑地接近零。同样,它可使得摩擦力随着切向相对位移逐渐增加而平滑地接近动摩擦力。
Δxt 是切向相对位移,
δ 是基于接触刚度和动摩擦力计算的容差。