Tato část obsahuje seznam problémů ověření výsledků Generátoru tvarů. Vždy, když je to možné, je důležité porovnat výsledky Generátoru tvarů se známými nebo teoretickými řešeními, a určit tak, zda lze jeho výsledky spolehlivě použít. Tato funkce je k dispozici v aplikaci Inventor 2016 R2 zákazníkům programu Subscription.
Krychle s tahovým napětím
V tomto problému je horní část krychle zatížena tahovým napětím. Čtyři rohy spodního povrchu krychle jsou zavazbeny ve směru zatížení, ale mají volnost posunu v rovině.
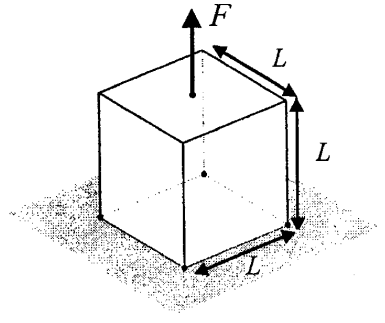

Pomocí Generátoru tvarů lze reprodukovat očekávaný výsledek. Všimněte si, že při použití omezujících podmínek posunu jsou v dolní části krychle zachovány horizontální tyče, což je v souladu s publikovanými výsledky [1].

Nyní upravíme omezující podmínky tak, že všechna posunutí ve čtyřech rozích dolního povrchu budou fixována (homogenní Dirichletova podmínka). Podle očekávání by se měl zobrazit tvar obsahující pouze čtyři diagonální členy [1].

Nosník s převislým koncem
V tomto problému je nosník s převislým koncem (D = 40, V = 25, Š = 1) zatížen bodovým zatížením působícím na konec převislé části nosníku. Bodové zatížení působí v polovině výšky konce převislé části nosníku. Nosník je vytvořen z izotropního materiálu s Youngovým modulem přesnosti 106 a Poissonovou konstantou 0,25.
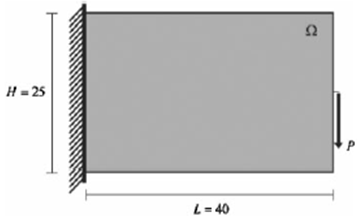
Níže uvedené publikované výsledky zobrazují optimální geometrii nosníku tvořeného 50 % hmoty původního návrhu pro proměnné minimální povolené průměry členů [2].
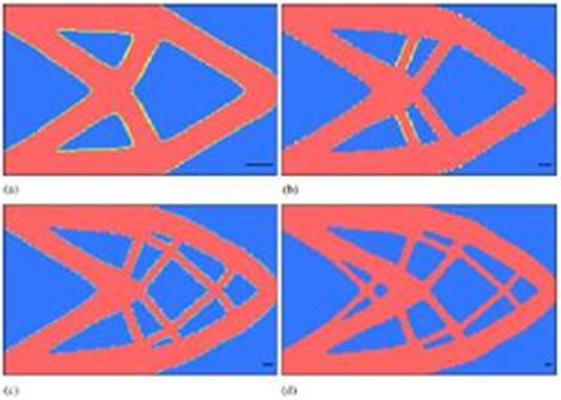
Pomocí Generátoru tvarů lze reprodukovat výsledek velmi podobný případu (b), ve kterém má minimální průměr členu hodnotu 2. Generátor tvarů aktuálně neumožňuje pracovat s minimální velikostí členu. Chcete-li vytvořit součást s tenkými členy, je nutné použít síť s vyšším rozlišením jako v ukázce níže.
Výsledek Generátoru tvarů obsahuje jeden viditelný rozdíl: materiál ponechaný na připevněné straně nosníku (vlevo). Protože v tomto umístění byly použity omezující podmínky, materiál podél této plochy byl automaticky zachován. Plochy se zatíženími a vazbami jsou při spuštění Generátoru tvarů automaticky zachovány.

Most
V tomto problému je cílem určit podpůrnou strukturu potřebnou k podpoře jednotně distribuovaného zatížení působícího na plochu. Jak je znázorněno na obrázku níže, v dolní části struktury existují tři pevné vazby [1].
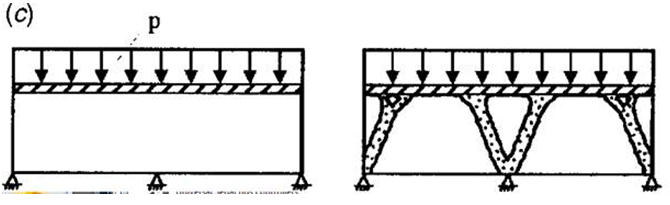
Pomocí Generátoru tvarů tuto strukturu vymodelujeme jako nosník s jednotně distribuovaným zatížením působícím na jeho horní plochu. Tři pevné vazby se použijí u dolní části nosníku, jedna na každé straně a jedna v polovině jeho délky. Níže uvedený výsledek odpovídá publikovanému řešení. Vygenerovaný tvar má formu mostovky na dvou podpůrných obloucích, které přenášejí tlakové zatížení na pevné vazby.

Hemisférická skořepina
V tomto problému je analyzována tenká hemisférická skořepina. Skořepina má v horní části díru, kolem které je použito tlakové zatížení. Posunutí ve směru osy Y jsou fixována k dolní hraně hemisféry. Posunutí ve směrech os X a Z jsou fixována kolem okrajů díry v horní části hemisféry [3].
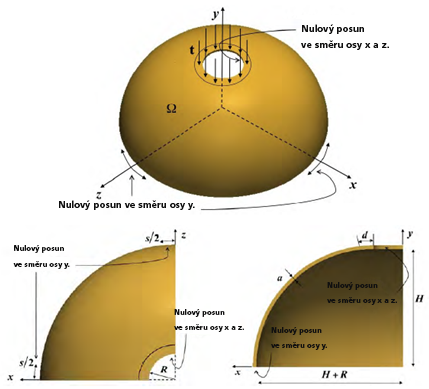
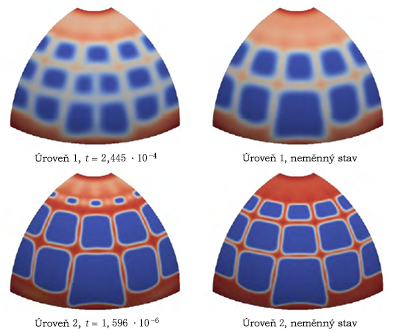

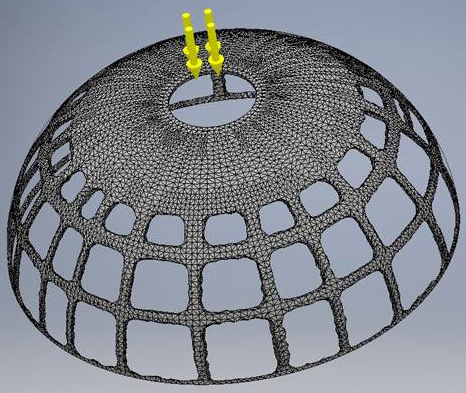
Pomocí Generátor tvarů lze reprodukovat publikovaný výsledek. Ačkoliv se vygenerovaný výsledek shoduje s očekávaným do velké míry, u dolního okraje hemisféry se v některých ohledech liší. Ve výsledku Generátoru tvarů je zachována tenká vrstva materiálu v místě použití omezujících podmínek. Publikované výsledky obsahují mnohem silnější pruh materiálu u dolní hrany hemisféry. Publikované výsledky také obsahují jistou varianci tloušťky tohoto pruhu materiálu, pravděpodobně z důvodu použití omezujících podmínek symetrie.
Reference
- Eschenauer, H.A., and Olhoff, N. (2001). Topology Optimization of Continuum Structures. Journal of Applied Mechanics Reviews. 54(4): 372.
- Guest, J.K., Prevost, J.H., and Belytschko, T. (2004). Achieving Minimum Length Scale in Topology Optimization Using Nodal Design Variables and Projection Functions. International Journal for Numerical Methods in Engineering. 61(2): 238-254.
- Dede, L., Borden, M.J., and Hughes, T.J.R. (2012) Isogeometric Analysis for Topology Optimization with a Phase Field Model. Archives of Computational Methods in Engineering. 19(3): 427-465.