Das MCT-Kriterium basiert auf der Mehrphasen-Kontinuumstheorie 39.40 (MCT). Das Mehrphasen-Konzept erweitert den Begriff der Phase, wobei deutlich unterschiedliche Materialien zusammen in einem repräsentativen Volumenelement (RVE) koexistieren. Eine solche Erweiterung ist überall da natürlich, wo mindestens zwei klar identifizierbare Konstituenten mit erheblich unterschiedlichen Materialeigenschaften vorhanden sind. Daher kann ein unidirektionales faserverstärktes Verbundmaterial als zwei interagierende Kontinua (ein Faserkontinuum und ein Matrixkontinuum) angesehen werden, die innerhalb eines entsprechend gewählten repräsentativen Volumenelements des Verbundmaterials koexistieren.
In der traditionellen Kontinuumsmechanik (wie sie auf faserverstärkte Verbundstrukturen angewandt wird) liegt der Schwerpunkt auf der Entwicklung von Beziehungen zwischen verschiedenen Verbunddurchschnittsgrößen (z.B. Spannung, Dehnung). Die Mehrphasen-Kontinuumstheorie (oder MCT) verbessert die traditionelle Kontinuumsmechanik, indem der Fokus auf zwei zusätzliche Probleme erweitert wird: 1) die Entwicklung von Beziehungen zwischen verschiedenen Konstituentendurchschnittsgrößen von Interesse und 2) die Entwicklung von Beziehungen, die Verbunddurchschnittsgrößen mit Konstituentendurchschnittsgrößen verknüpfen.
MCT prognostiziert Ausfälle auf der Faser- und Matrixebene im Gegensatz zur Verbund- oder Lagenebene. Dies erfolgt durch das Abrufen der über das Volumen gemittelten Spannungszustände in der Faser und Matrix. Die Konstituentenspannungen sind eine Funktion der Verbundspannung und der Steifheit der Verbundfaser und -matrix.
Die MCT-Zerlegung
Die Faser- und Matrixspannungen werden über das folgende Verfahren zur Spannungs- und Dehnungszerlegung ermittelt. Der erste Schritt besteht in der Ermittlung des Dehnungszustands in der Matrix:
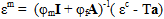
wobei φf und φm den Volumenanteil der jeweiligen Fasern und Matrix repräsentieren, I eine 6x6-Identitätsmatrix ist und A und a die mechanische und thermische Durchschnittsdehnung in den entsprechenden Konstituenten zuordnen. Sie sind wie folgt definiert:
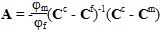
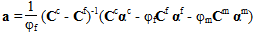
Die Dehnung in der Faser kann dann wie folgt ermittelt werden:
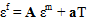
Jetzt lassen sich die Spannungszustände von Faser und Matrix berechnen:
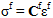
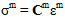
Die Konstituentenspannungen werden verwendet, um Ausfälle in Faser und Matrix separat auszuwerten.
MCT-Ausfallkriterium für Matrixkonstituenten
Die folgenden Annahmen werden bei der Entwicklung des Ausfallkriteriums für Matrixkonstituenten für unidirektionale Verbundwerkstoffe angewendet.
- Es wird davon ausgegangen, dass das Matrixversagen durch alle sechs Matrixdurchschnittsspannungskomponenten (
, 
, 
, 
, 
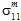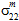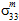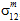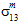und 
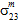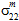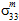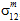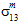) beeinflusst wird. - Es wird davon ausgegangen, dass das Matrixkonstituentenmaterial transversal isotrop ist. Daher lässt sich nicht unterscheiden, in welchem Maße und zum Matrixversagen beitragen, so wie auch nicht bestimmbar ist, wie unterschiedlich und zum Matrixversagen beitragen.
- Inwieweit die Matrixdurchschnittsnormalspannungen (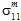, 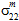und 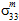) für das Matrixversagen verantwortlich sind, ist davon abhängig, ob es sich bei den Normalspannungen um Zug - oder Druckspannungen handelt.
Mit diesen vier grundlegenden Annahmen wird das Matrixausfallkriterium als quadratische Funktion der Matrixdurchschnittsspannungskomponenten ausgedrückt.
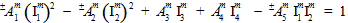
In der obigen Gleichung sind die Größen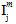 
(j=1,2,3,4) transversale isotrope Invarianten des Matrixdurchschnittsspannungszustands.
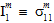
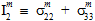
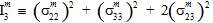
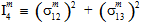
Die Größen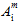 
(i=1,2,3,4,5) sind die Koeffizienten der Matrixausfallkriterien. Wenn ein hochgestelltes Symbol '±' vor einem Koeffizienten 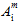steht, gibt das Symbol an, dass der numerische Wert 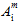davon abhängt, ob die zugeordneten Matrixdurchschnittsspannungen Zug- oder Druckspannungen sind. Damit stellt 
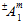zwei mögliche Werte dar. Für den Koeffizienten 
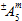gibt es tatsächlich vier mögliche Werte, je nachdem, ob 
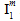positiv oder negativ ist und auch, ob 
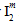positiv oder negativ ist. Daher enthält das Matrixausfallkriterium insgesamt zehn anpassbare Koeffizienten, die anhand der gemessenen Festigkeiten des Verbundmaterials festgelegt werden müssen.
MCT-Ausfallkriterium für Faserkonstituenten
- Es wird angenommen, dass Faserausfälle von den gemittelten Spannungskomponenten für die Faserkonstituente
, 
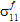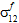und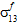 
beeinflusst werden. - Es wird angenommen, dass Faserausfälle von den gemittelten Spannungskomponenten für die Faserkonstituente
, 
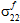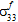und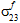 
unabhängig sind. - Der Beitrag von 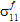zur Produktion von Faserausfällen ist davon abhängig, ob 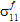eine Zug - oder Druckspannung darstellt.
- Es wird davon ausgegangen, dass das Faserkonstituentenmaterial transversal isotrop ist. Deshalb ist nicht bestimmbar, in welchem Maße 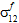und 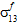zum Faserversagen beitragen.
Mit diesen vier grundlegenden Annahmen wird das Faserausfallkriterium als quadratische Funktion der Faserdurchschnittsspannungskomponenten ausgedrückt.
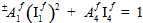
Die Größen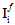 
(i = 1,4) sind zwei der transversal isotropen Invarianten des faserbezogenen durchschnittlichen Spannungszustands.
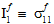
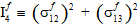
Die Größen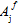 
(j 1,4) sind die anpassbaren Koeffizienten des Faserausfallkriteriums. Wenn ein hochgestelltes Symbol '±' vor einem Koeffizienten 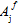steht, gibt das Symbol an, dass der Wert 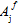davon abhängt, ob die zugeordneten Faserdurchschnittsspannungen Zug- oder Druckspannungen sind. Damit stellt 
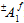zwei mögliche Werte dar. Daher enthält das Faserausfallkriterium insgesamt drei anpassbare Koeffizienten, die anhand der gemessenen Festigkeiten des Verbundmaterials festgelegt werden müssen.