Validierungsprobleme

Dieser Abschnitt enthält eine Liste der Validierungsprobleme für den Formen-Generator. Wenn möglich, sollten Sie die Lösungen des Formen-Generators mit bekannten oder theoretischer Lösungen vergleichen, um zu verstehen, in welchen Bereichen dieser zuverlässig verwendet werden kann. Verfügbar in Inventor 2016 R2 - Subscription-Kunden.

Spannung - Würfel

Bei diesem Problem wird die Oberseite eines Würfels unter Spannung belastet. Für die vier Ecken der unteren Fläche des Würfels besteht in Richtung der Last eine Abhängigkeit, sie sind jedoch frei, um in der Ebene zu gleiten.

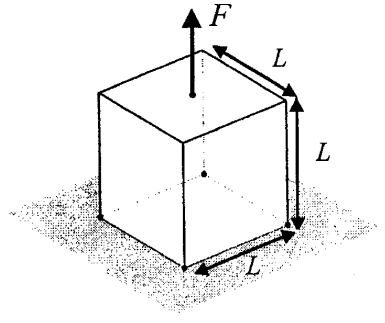
Mithilfe des Formen-Generators können wir das erwartete Ergebnis reproduzieren. Beachten Sie, dass zusammen mit den gleitenden Begrenzungsbedingungen die horizontalen Balken auf der Unterseite des Würfels vorhanden sind, was mit den publizierten Ergebnissen übereinstimmt [1].

Jetzt ändern wir die Begrenzungsbedingungen, sodass alle Verschiebungen an den vier Ecken an der unteren Fläche des Würfels festgelegt werden (homogene Dirichlet-Bedingung). Wir erwarten, dass eine Form mit nur den vier diagonalen Elementen angezeigt wird [1].

Auslegerbalken

Bei diesem Problem wird ein Auslegerbalken (L = 40, H = 25 B = 1) belastet, indem eine Punktlast auf das freie Ende der Trägers wirkt. Die Punktlast wird halb bis zum freien Ende des Trägers angewendet. Der Träger wurde aus isotropem Material mit einem Elastizitätsmodul von 10⁶ und einer Poisson-Zahl von 0,25 hergestellt.

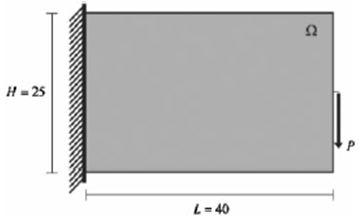
Die publizierten Ergebnisse unten zeigen die optimale Trägergeometrie mit 50 % des ursprünglichen Konstruktionsdomänenvolumens für unterschiedliche minimal zulässige Elementdurchmesser [2].

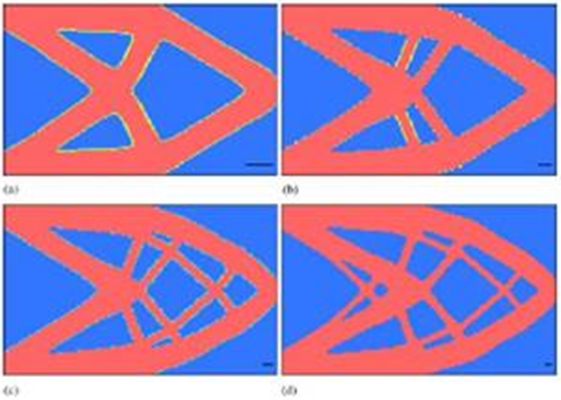
Mithilfe des Formen-Generators sind wir in der Lage, ein sehr ähnliches Ergebnis wie Fall (b) zu reproduzieren, bei dem der minimale Elementdurchmesser bei 2 liegt. Der Formen-Generator gibt aktuell keine minimale Elementgröße vor. Um ein Bauteil mit dünnen Elementen zu erstellen, sollten Sie ein Netz mit höherer Auflösung verwenden, wie unten veranschaulicht.

Ein erheblicher Unterschied beim Formen-Generator-Ergebnis ist das Material, das am festgelegten (linken) Ende des Trägers verbleibt. Da eine Begrenzungsbedingung an dieser Position angewendet wurde, wurde das Material entlang dieser Fläche automatisch beibehalten. Flächen mit angewendeten Lasten und Abhängigkeiten werden beim Ausführen des Formen-Generators automatisch beibehalten.

Überbrücken

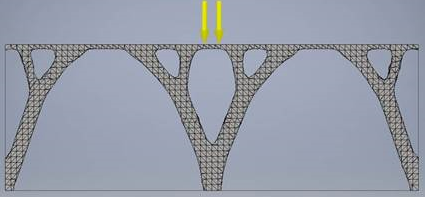
Bei diesem Problem möchten wir das erforderliche Tragwerk für eine gleichmäßig verteilte Last, die auf eine Fläche wirkt, ermitteln. Wie in der Abbildung unten gezeigt, gibt es drei festgelegte Abhängigkeiten an der Unterseite der Struktur [1].

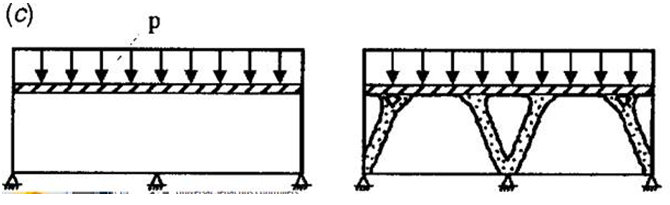
Mithilfe des Formen-Generators modellieren wir diese Struktur als Träger mit einer gleichmäßig verteilten Last, die an der Oberseite angewendet wird. Die drei festgelegten Abhängigkeiten werden an der Unterseite des Trägers angewendet - eine an jedem Ende und eine auf halber Strecke. Das Ergebnis unten stimmt mit der publizierten Lösung überein. Die generierte Form entspricht einer Brückentafel auf zwei tragenden Bogen, die die Drucklast auf die festgelegten Abhängigkeiten übertragen können.

Halbkugelförmige Wandung

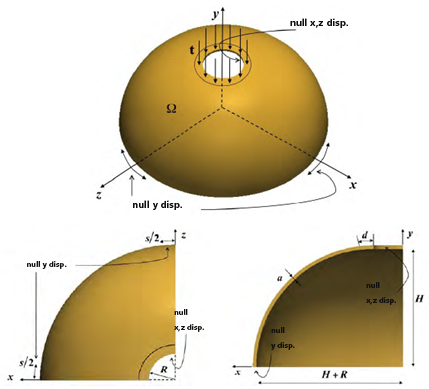
Bei diesem Problem wird eine dünne, halbkugelförmige Wandung untersucht. Die Wandung hat oben eine Bohrungsöffnung, um die eine Drucklast angewendet wird. Die y-Verschiebungen sind an der Unterkante der Halbkugel festgelegt. Die x- und z-Verschiebungen sind um die Bohrungsöffnung auf der Oberseite der Halbkugel festgelegt [3].

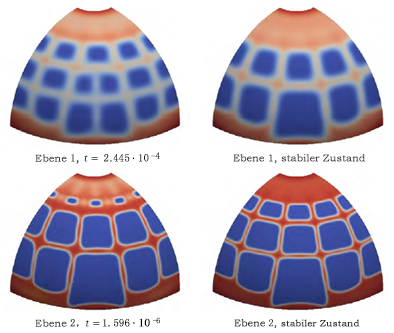
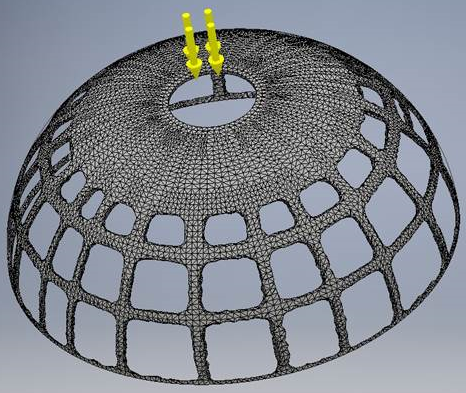
Mithilfe des Formen-Generators können wir das publizierte Ergebnis reproduzieren. Der Großteil des generierten Ergebnisses stimmt mit den publizierten Ergebnissen überein. Es gibt jedoch auch einige deutliche Unterschiede an der Unterkante der Halbkugel. Im Formen-Generator-Ergebnis bleibt nur eine dünne Schicht an Material dort übrig, wo die Begrenzungsbedingungen angewendet werden. Die publizierten Ergebnisse zeigen ein viel dickeres Materialband an der Unterkante der Halbkugel. Die publizierten Ergebnisse zeigen auch einige Abweichungen bei der Dicke dieses Materialbandes, wahrscheinlich aufgrund der Symmetrie der verwendeten Begrenzungsbedingungen.

Referenzen

1. Eschenauer, H.A. und Olhoff, N. (2001) "Topology Optimization of Continuum Structures," Journal of Applied Mechanics Reviews. 54(4): 372.
2. Guest, J.K., Prevost, J.H. und Belytschko, T. (2004) "Achieving Minimum Length Scale in Topology Optimization Using Nodal Design Variables and Projection Functions," International Journal for Numerical Methods in Engineering. 61(2): 238-254.
3. Dede, L., Borden, M.J. und Hughes, T.J.R. (2012) "Isogeometric Analysis for Topology Optimization with a Phase Field Model," Archives of Computational Methods in Engineering. 19(3): 427-465.