Die finite Elementformulierung wird verwendet, um den in der transienten Wärmeableitungsgleichung verwendeten Wärmequellenbegriff zu ermitteln.
Die Gleichungen, die das elektromagnetische Phänomen beschreibt, finden Sie unter Modellieren von elektromagnetischen Feldern. Die finite Elementformulierung wird zur Lösung der Gleichung (19) auf dieser Seite verwendet:
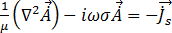(19)
um den Wärmequellenbegriff zu ermitteln, Gleichung 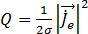(21)
(21)
wird vom Temperierungs-Solver zur Lösung der Gleichung (22) verwendet:
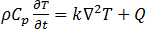(22)
Da es sich bei der Gleichung (19) um eine vereinfachte zeitharmonische Gleichung handelt, müssen das magnetische Vektorpotenzial,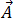 
, und die Wirbelströme, 
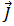, in komplexen Zahlen ausgedrückt werden:
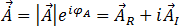(23)
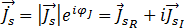(24)
wobei sich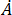 
und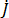 
auf eine kartesische Komponente der zu ermittelnden Begriffe beziehen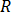, und 
und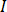 
tiefgestellte Zeichen der realen und virtuelle Komponenten der komplexe Zahl darstellen.
Der Galerkin-Ansatz wird bei Gleichung (19) separat für jede X-, Y- und Z-Komponenten eines Vektors angewandt.
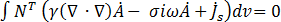(25)
resultiert in 3 Gleichungen der folgenden Form:
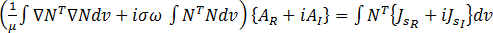(26)
wobei sich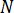 
auf Formfunktionen bezieht und 
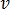auf das Volumen des Elements. Gleichung 26 wird für jedes Tetraederelement für reelle und virtuelle Komponenten der unbekannten, kartesischen Komponenten des magnetischen Vektorpotenzials, 
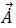, gelöst. Damit verfügt 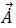über sechs Freiheitsgrade, die gelöst werden müssen.