Nur Tetraeder-Volumenkörperelemente sind derzeit in der Software verfügbar. Sowohl lineare als auch parabolische Typen sind verfügbar. Volumenkörper werden verwendet, um dicke Strukturen zu modellieren, bei denen Spannung in alle Richtungen wichtig und von Interesse ist.
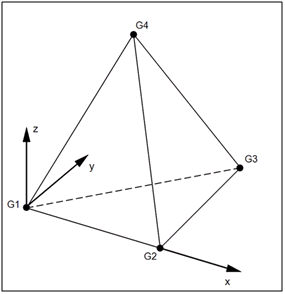
Linear
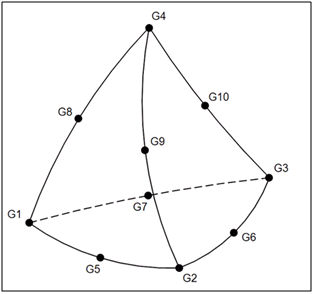
Parabolisch
Elementgeometrie
Auf dem Bild des linearen Volumenkörper-Tetraederelements kann man erkennen, dass der Ursprung des Koordinatensystems auf G1 liegt. Die X-Achse des Elements ist durch den Vektor G1 –G2 definiert. Die Y-Achse des Elements liegt orthogonal zur X-Achse und befindet sich in der G1-G2-G3-Ebene. Die Z-Achse des Elements ergibt sich aus der Überkreuzung von Element X und Element Y.
Formulierungsoptionen
In dieser Software sind derzeit zwei Arten von Volumenkörper-Tetraederelementen verfügbar: lineare und parabolische. Lineare Elemente verfügen nur über 4 Knoten. Parabolische Volumenkörper-Tetraederelemente verfügen über 10 Knoten. Lineare Elemente sind steifer und parabolische Elemente sind flexibler.
Freiheitsgrade
Volumenkörperelemente verfügen über keine Rotations-Freiheitsgrade an jedem Knoten. Ein Moment oder ein Drehmoment, das auf die Fläche eines Volumenkörperelementnetzes (linear oder parabolisch) angewendet wird, ergibt eine Leer- oder Null-Ausgabe. Es muss eine Kräfteverbindung oder ein starres Element verwendet werden, um ein Drehmoment oder ein Moment auf eine Fläche mit einem zugeordneten Volumennetz anzuwenden.
Elementausgabe
Alle Volumenelement-Ergebnisse sind im globalen rechteckigen Koordinatensystem angegeben. Die Volumenelement-Ergebnisse sind das Ergebnis der Mittelung der Gaußschen Punktergebnisse. Die Knotenergebnisse (oder Eckergebnisse) werden an den Knoten mithilfe des nächstpositionierten Gaußschen Punkts und der Formfunktionen für die Elemente extrapoliert (weitere Informationen zur Elementtheorie finden Sie in jedem Finite-Element-Lehrbuch).