Freiheitsgrade (degrees of freedom, DOF) sind die grundlegenden Variablen, die für Finite-Element-Analysen gelöst werden. Jede Elementgruppe verfügt über verschiedene Freiheitsgrade.
Ein Freiheitsgrad entspricht einer Translation oder Drehung an jedem Knoten eines Elements. Es gibt bis zu sechs Freiheitsgrade pro Knoten je nach Elementtyp.
- Translationsrichtung 1 (oft X-Translation)
- Translationsrichtung 2 (oft X-Translation)
- Translationsrichtung 3 (oft X-Translation)
- Drehungsrichtung 4 (oft X-Drehung)
- Drehungsrichtung 5 (oft Y-Drehung)
- Drehungsrichtung 6 (oft Z-Drehung)
In Bezug auf das zylindrische Koordinatensystem würden die Freiheitsgrade wie folgt entsprechen:
- Freiheitsgrad 1 entspricht der Translation entlang der Richtung r
- Freiheitsgrad 2 entspricht der Translation entlang der Richtung θ
- Freiheitsgrad 3 entspricht der Translation entlang der Richtung z
- Freiheitsgrad 4 entspricht der Drehung in Richtung r
- Freiheitsgrad 5 entspricht der Drehung in Richtung θ
- Freiheitsgrad 6 entspricht der Drehung in Richtung z
Aus diesem Grund werden Freiheitsgrade oft in Form der Ziffern 1,2,3,4 usw. beschrieben.
Volumenkörperelemente verfügen über drei Freiheitsgrade pro Knoten. Volumenkörper unterstützen nur translationale Freiheitsgrade an jedem Knoten. Daher können Momente nicht direkt auf Volumenkörper angewendet werden. Ein Moment wirkt auf die Rotations-Freiheitsgrade.
Jedes Raster (G1-G4) in der Abbildung unten kann nur konvertieren. Dies ist die Formulierung für die Volumenkörperelemente im Autodesk Nastran-Solver.
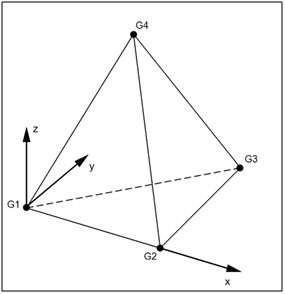
Schalenelemente haben fünf Freiheitsgrade pro Knoten mit quasi einem sechsten Freiheitsgrad.
Linienelemente (in dieser Software) haben über sechs Freiheitsgrade pro Knoten.
Drehungen, Verschiebungen und Temperaturen werden an den Knoten gelöst. Einige Elemente können mehr Knoten pro Element haben, indem die Reihenfolge der Interpolation erhöht wird. Die Vorgabekonfiguration für Volumenkörperelemente ist parabolisch, hat jedoch eine Option für eine lineare Reihenfolge. Die Vorgabekonfiguration für Schalenelemente ist linear, hat jedoch eine parabolische Option. Die Vorgabe für Linienelemente ist linear und verfügt über keine andere Konfiguration.
Um grundlegende Größen zu berechnen, integriert der Solver das Volumen des Elements mit den angegebenen Punkten als Gaußschen Punkten und verwendet somit eine Gaußsche Quadratur, um diese Integration durchzuführen. Durch Erhöhen der Elementreihenfolge (Auswahl parabolisch und linear) erhöht der Solver die Anzahl der Gaußschen Punkte, die in diesem Prozess verwendet werden.