Das Dialogfeld Materialeigenschafteneingabe für die hyperelastischen Modelle und die Modelle aus Schaummaterial enthält die Routine Kurvenanpassung. Die Kurvenanpassung wird verwendet, um die Konstanten für das mathematische Materialmodell zu bestimmen, indem eine optimale Berechnung der vom Benutzer gelieferten Spannungs-/Dehnungsdaten für das Material durchgeführt wird. Beachten Sie, dass keine Lösung den Testdaten exakt entsprechen wird! Variationen der Tests und Materialien führen zu Streuungen in den Testdaten. Daher ist ein hohes Maß an Genauigkeit in der Kurvenanpassungsroutine in den meisten Situationen nicht gerechtfertigt. Wichtig ist, dass die Ergebnisse der Kurvenanpassungsroutine den Testdaten im Interessenbereich entsprechen.
Jedes Materialmodell bietet Optionen speziell für Ihre Anforderungen. Einige der im Folgenden beschriebenen Elemente sind je nach Materialmodell irrelevant. Das allgemeine Layout des Dialogfelds Kurvenanpassung wird in Abbildung 1 dargestellt und unten beschrieben.
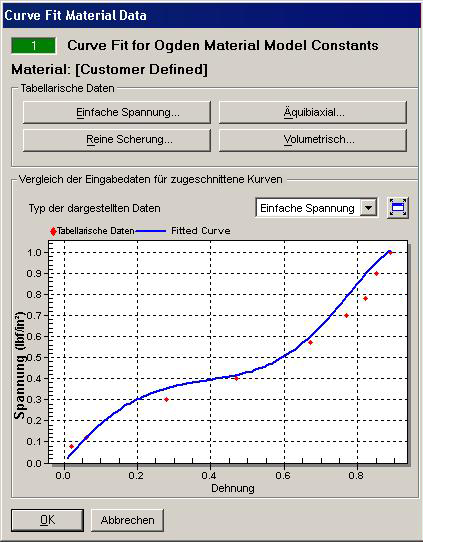
Abbildung 1L: Dialogfeld Kurvenanpassung für Ogden (linke Hälfte des Dialogfelds)
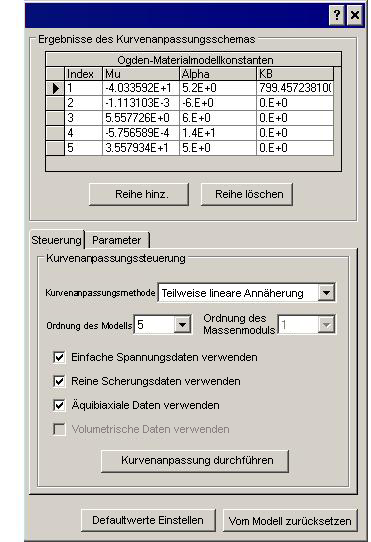
Abbildung 1R: Dialogfeld Kurvenanpassung für Ogden (rechte Hälfte des Dialogfelds)
Abschnitt Tabellendaten:
Dieser Abschnitt wird verwendet, um die bekannten Spannungs-/Dehnungsdaten für das Material einzugeben. Es ist wichtig, die folgenden Anweisungen beim Abrufen der Testdaten zu berücksichtigen:
- Um genaue Konstanten für die Analyse abzuleiten, müssen die bei der Kurvenanpassung eingegebenen Spannungs-/Dehnungsdaten den gesamten Lastbereich abdecken, der in der Analyse vorkommt. Wenn am Bauteil beispielsweise Scherspannungen zusätzlich zu Spannung und Komprimierung auftreten, müssen reine Spannungs-/Dehnungsdaten eingegeben werden. Einfache Spannung selbst ist nicht ausreichend, um das Verhalten des Materials in solchen Situationen ordnungsgemäß zu modellieren. Das gleiche gilt für die anderen Typen von Tabellendaten.
- Da die Daten aus allen Experimenten zusammen zum Ableiten der Materialkonstanten verwendet werden, ist es wichtig, dass das getestete Material aus dem gleichen Stapel stammt. Andernfalls verfälschen die Variationen in der Materialproduktion die Testdaten.
- Viele Elastomere ändern das Verhalten während der ersten Ladezyklen. Außerdem ändert sich die Spannungs-/Dehnungskurve, wenn die maximal auftretende Belastung erhöht wird. Daher sollte das Material einen in der Analyse erwarteten Dehnungswert ergeben, und die Last sollte so lange wiederholt werden, bis sich das Verhalten stabilisiert.
- Falls noch nicht als solcher vorhanden, müssen die Spannungs-/Dehnungsdaten möglicherweise in eine Nulldehnung geändert werden. Wenn Sie ein hyperelastisches Material auf einen neuen Dehnungsgrad strecken, kehrt es häufig nicht in die ursprüngliche Dehnung zurück. (Dies gilt unabhängig davon, ob es sich um den ersten Durchlauf handelt oder ob bereits mehrere Durchläufe stattfanden. Es ist der neue, höhere Dehnungsgrad, der zu einer neuen permanenten Verformung führt.) Die permanente Verformung, die im Test gemessen wird, muss aus den Dehnungswerten entfernt werden. Genauso muss sich die sich ändernde Querschnittfläche aufgrund der dauerhaften Verformung in der ursprünglichen Fläche widerspiegeln, die zum Berechnen der Spannung verwendet wird. Diese beiden Korrekturen ändern die Spannungs-/Dehnungskurve wieder auf einen Anfangswert von 0,0.
- Abhängig vom verwendeten Materialmodell ändern die meisten hyperelastischen Materialmodelle ihre Eigenschaften aufgrund wiederholter Lasten nicht. Jeder Analysedurchlauf folgt der berechneten Spannungs-/Dehnungskurve. Deshalb müssen die Testdaten ausgewählt oder gemittelt werden, um dem analytischen Verhalten zu entsprechen.
- Die meisten hyperelastischen Materialmodelle folgen der gleichen Spannungs-/Dehnungskurve zum Belasten und Entlasten. Es tritt keine dauerhafte Verformung auf.
Die Typen der Testdaten, die eingegeben werden können, sind folgende:
- Schaltfläche Einfache Spannung: Gibt die Spannungs-/Dehnungsdaten aus einem einfachen Spannungstest ein. Die Testdaten müssen so sein, dass ein reiner Zustand der Zugverformung gemessen wird. In den Testdaten ist keine laterale Abhängigkeit vorhanden. Nur der Spannungszweig wird eingegeben. Die Komprimierungsdaten werden von den Äquibiaxialdaten abgeleitet.
- Schaltfläche Äquibiaxial: Gibt die Spannungs-/Dehnungsdaten aus einer Äquibiaxial- oder einer gleichen Biaxialausdehnung an. Dies sind die Testdaten, die zum Reproduzieren der Druckspannung-Dehnung verwendet werden. Durch das gleichmäßige Ziehen in beide Richtungen wird ein Zustand der Belastung erreicht, die der reinen Komprimierung entspricht.
- Schaltfläche Reine Scherung: Gibt die Spannungs-/Dehnungsdaten aus einem reinen Scherdehnungstest an. Für hyperelastische Materialien handelt es sich dabei in der Regel um ein breites Zugmaterial. Da das Material jedoch fast nicht komprimierbar ist, besteht ein Zustand der reinen Scherspannung.
- Schaltfläche Einfache Scherung: Geben Sie die Spannungs-/Dehnungsdaten aus einem einfachen Schertest ein.
- Schaltfläche Volumetrisch: Gibt die Druck-Dehnungsdaten aus einem volumetrischen Komprimierungstest an. Diese Daten werden verwendet, um das Kompressionsmodul zu ermitteln. Für hyperelastische Materialien ist dies für Situationen wichtig, in denen das Material nur geringfügig komprimierbar oder das Bauteil überbestimmt ist. Das Kompressionsmodul ist in der Regel zwei bis drei Größenordnungen größer als das Schermodul. Für Schaummaterialien sind die volumetrischen Daten wichtig, um die Komprimierbarkeit des Schaums zu erfassen.
Klicken Sie auf eine der Schaltflächen im Abschnitt Tabellarische Daten. Dadurch wird ein neues Dialogfeld angezeigt, in dem die Spannungs- und Dehnungsdaten eingegeben werden. Folgende Steuerelemente stehen zur Verfügung:
- Pulldown-Menü Dehnungsformat: Wählen Sie das Format für die Dehnungsdaten. Nominale Dehnung wird aus (Änderung der Länge) /(ursprüngliche Länge) berechnet, und Ausdehnung wird aus (aktuelle Länge) /(ursprüngliche Länge) = 1 + (nominale Dehnung) berechnet.
- Feld Effektiver Poisson-Koeffizient (nur Schaummaterialmodelle): Wenn der Poisson-Koeffizient bekannt und die Querdehnung unbekannt ist, geben Sie einen effektiven Poisson-Koeffizienten ein. Diese Eingabe wird zusammen mit der Schaltfläche Auffüllen und der in der Tabellenkalkulationstabelle eingegebenen primären Dehnung verwendet, um die Querdehnung zu berechnen.
- Schaltfläche Auffüllen: Durch Klicken auf diese Schaltfläche werden die Werte für die Spalte Dehnung, Quer in der Tabelle auf der Grundlage des Feldes Effektive Poissonsche Konstante und der Spalte Dehnung, Primär berechnet.
- Kontrollkästchen Querspannungseingabe: Für Schaummaterialien können die Scher- und Querspannung unterschiedliche Werte aufweisen. Wenn diese Option aktiviert ist (sie wird nur bei den einfachen Schertestdaten angezeigt), wird die Querspannung nur in der Spannungs-/Dehnungstabellenkalkulation eingegeben. Wenn die Option nicht aktiviert ist, wird angenommen, dass die Querspannung der Scherspannung entspricht, und die Spalte ist nicht in der Tabellenkalkulation enthalten.
- Tabellenkalkulation Spannungs-/Dehnungsdaten oder Volumetrische Druck-Dehnungsdaten: Geben Sie die angeforderte Spannung und Dehnung (abhängig vom Datentyp) ein. Die Konstruktionsspannung/-dehnung sollte verwendet werden (basierend auf der ursprünglichen Länge und Fläche). Die Werte müssen in aufsteigender Reihenfolge eingegeben werden, basierend auf der zweiten Spalte (im allgemeinen Dehnung für hyperelastische Materialien und Spannung für Schaummaterialien).
- Kontrollkästchen Auto-korrektur: Für volumetrische Druck-Dehnungsdaten müssen die Zeichen für Dehnung und Druck richtig sein, um das korrekte Kompressionsmodul zu berechnen. Wenn diese Option aktiviert ist, ändert der Gleichungslöser ggf. das Zeichen des eingegebenen volumetrischen Drucks, um die richtige Berechnung zu erhalten. Ist diese Option nicht aktiviert, sollten die Dehnungswerte negativ sein und der Druck positiv.
- Schaltflächen Zeile hinzufügen und Zeile löschen: Fügt eine Zeile am Ende der Tabelle ein und löscht die aktuelle Zeile entsprechend.
- Schaltfläche Sortieren: Sortiert die Spannungs-/Dehnungsdaten in aufsteigender Reihenfolge anhand der zweiten Spalte (in der Regel der Dehnungswert für hyperelastische Materialien oder der Spannungswert für Schaummaterialien).
- Schaltfläche Importieren: Importiert die Spannungs-/Dehnungsdaten in eine kommagetrennte Datei (CSV). Die Datei sollte im gleichen Format wie die Tabellenkalkulation vorliegen, jedoch ohne die Indexspalte. Beachten Sie, dass alle vorhandenen Daten durch die importierten Daten ersetzt werden. Für die Schaummaterialmodelle können zwei oder drei Spalten importiert werden. Wenn die dritte Spalte - Dehnung, Quer - nicht in der Datendatei mit kommagetrennten Werten enthalten ist, wird die Spalte auf Null gesetzt. Verwenden Sie den effektiven Poisson-Koeffizienten und die Schaltfläche Auffüllen, um Schätzwerte zu erstellen. Achtung: Einige der Spannungs-/Dehnungstabellenkalkulationen verwenden die Spannung in der ersten Spalte und andere verwenden die Dehnung. Die Daten müssen in der CSV-Datei in der entsprechenden Spalte vorliegen, um der Tabelle zu entsprechen.Tipp: Die Werte in der kommagetrennten Datei werden mit den aktiven Anzeigeeinheiten importiert. Ändern Sie ggf. die Anzeigeeinheiten, bevor Sie die Daten importieren. Ein Wert von beispielsweise 314 wird als 314 psi importiert, wenn die Anzeigeeinheiten auf Pfund und Zoll festgelegt werden, und 314 Pa, wenn die Anzeigeeinheiten Newton und Meter lauten
- Schaltfläche Exportieren: Speichert die eingegebenen Spannungs-/Dehnungsdaten in eine kommagetrennte Datei.
Registerkarte Parameter
Einige der Materialmodelle benötigen Schätzwerte, um die Annäherungsanpassungsroutine zu starten. Diese Parameter werden auf der Registerkarte Parameter eingegeben und sollten bereitgestellt werden, bevor Sie mit der Kurvenanpassung beginnen. Welche Parameter eingegeben werden, hängt vom Algorithmus der Kurvenanpassungsmethode ab, die auf der Registerkarte Steuerelemente ausgewählt wurde.
Teilweise lineare Annäherung: Diese Suchmethode berechnet alle möglichen Kombinationen von Koeffizienten basierend auf den ersten Schätzungen und meldet die Kombination, die den Mindestfehler ausgibt. Da alle Kombinationen berechnet werden, kann diese Methode länger dauern als die anderen Methoden, insbesondere, wenn ein großer Inkrementwert verwendet wird. Beachten Sie außerdem, dass Lösungen außerhalb des Bereichs nicht getestet werden, sodass eine Lösung mit einem kleineren Fehler vorhanden sind. Wenn die angezeigten Ergebnisse nicht zu den Daten passen, verwenden Sie einen anderen Bereich. Die Eingabe lautet wie folgt:
- Werte Schätzung oder Geschätzt: Geben Sie den ursprünglichen Schätzwert für den Parameter an. Diese Eingabe ist die Mitte des berechneten Bereichs. Beachten Sie, dass der Wert 0 für einige Werte in einigen Materialmodellen unzulässig ist. Beispielsweise verwendet die mögliche Gleichung für das Ogden-Materialmodell den Parameter Alpha im Nenner, sodass das Teilen durch Null unzulässig ist. Wenn derartige Fälle während der Anpassungsroutine auftreten, wechseln die Parameter in die vordefinierten Standardwerte.
- Bereichswert: Geben Sie den Bereich der geschätzten Werte ein, die getestet werden (vom niedrigsten zum höchsten Testwert). Der kleinste Wert ist gleich dem geschätzten Wert minus der Hälfte des Bereichs, und der höchste Wert ist gleich dem geschätzten Wert plus der Hälfte des Bereichs.
- Wert Inkrement: Dies ist die Anzahl der Punkte zwischen dem niedrigsten und dem höchsten berechneten Wert. Damit ein Intervall von 20 für drei Parameter 20 ^ 3 = 8000-Kombinationen ergibt, von denen der minimale Fehler gemeldet wird.
Levenberg-Marquardt-Algorithmus, Gauss-Newton-Algorithmus und Eingeschränkte Optimierung: Diese Methoden beginnen beim ursprünglichen geschätzten Wert und ermitteln den ersten Mindestwert (Neigung der Fehlerfunktion ist Null) für die optimalen Gleichungen. Da möglicherweise zahlreiche Mindestwerte vorhanden sind, wenn mehrere Variablen beteiligt sind, ist die Präzision der Lösung abhängig von den ersten Schätzungen. Siehe Abbildung 2.
- Werte Schätzung oder Geschätzt: Geben Sie die erforderlichen Näherungswerte für alle Konstanten ein. Es empfiehlt sich, den Wert Null nicht zu verwenden. Außerdem sollte ein Wert ungleich Null für jeden geschätzten Wert entsprechend der Ordnung des Modells eingegeben werden. Bei der Berechnung eines Modells der fünften Ordnung sollten geschätzte Werte für die ersten 5 Konstanten eingegeben werden. Eine gute Schätzung sind die Ergebnisse aus einer anderen Kurvenanpassungsmethode. So sind z. B. die Konstanten mit der partiellen linearen Annäherungsmethode eine gute Schätzung für den Levenberg-Marquardt-Algorithmus. Da die Kurvenanpassung eine numerische Lösungsmethode ist, kann eine andere Schätzung zu einem anderen Kurvenanpassungsergebnis führen.
- Feld Maximale Iteration: Geben Sie die maximale Anzahl der anzuwendenden Wiederholungen ein. Wenn keine Lösung gefunden wird, bevor die maximale Anzahl Wiederholungen erreicht ist, wird eine Fehlermeldung während der Kurvenanpassungsroutine ausgegeben.
- Feld Toleranz: Geben Sie die für die Kurvenanpassungsroutine zu verwendende Toleranz ein. Die Lösung gilt als konvergiert, wenn die Konstanten sich um einen Wert kleiner als die Toleranz von einer Wiederholung zur nächsten ändern.
Fehler
 Wert
Wert
Registerkarte Steuerung
Abschnitt Kurvenanpassungssteuerung
Die Kurvenanpassungssteuerung wird verwendet, um anzugeben, wie die Testdaten für die Kurvenanpassungsroutine verwendet werden sollen, z. B. welche Testdaten in die Kurvenanpassungsberechnung einbezogen werden sollen, die Ordnung des Modells und die Methode für die Anpassung der Daten.
- Kontrollkästchen Daten verwenden: Aktivieren Sie die Kontrollkästchen für die Testdaten, die in der Kurvenanpassungsroutine verwendet werden sollen. Alle eingegebenen Testdaten sollten verwendet werden. Der einzige Grund, warum ein bestimmter Datensatz nicht verwendet werden soll, ist, wenn ein Datensatz zu einer schlechten Anpassung der anderen Daten führt. In diesem Fall sollte eine andere Ordnung des Modells, eine andere Kurvenanpassungsmethode oder ein Materialmodell verwendet werden, um eine bessere Anpassung zu erhalten.
- Dropdown-Liste Kurvenanpassungsmethode: Wählen Sie eine numerische Methode für die optimale Anpassung an die Testdaten. Jede Methode führt zu einem anderen Satz von Konstanten; die Methode, die zu einer guten Anpassung an die Daten führt (visuell und im RMS) ist jene, die verwendet werden soll. Beachten Sie, dass der Levenberg-Marquardt Algorithmus und der Gauss-Newton-Algorithmus empfindlich auf die erste Schätzung reagieren können. Geben Sie diese auf der Registerkarte Parameter an. Die Methode Teilweise lineare Annäherung kann zum Ermitteln erster Schätzwerte für die Konstanten gut sein.
- Pulldown-Menü Ordnung des Modells: Wählen Sie die Ordnung des Modells für die Kurvenanpassungsroutine. Im Allgemeinen gilt: Je niedriger die Ordnung, desto schneller die Analyse, Modelle höherer Ordnung sind jedoch erforderlich, um eine bessere Anpassung an die Testdaten zu erhalten, insbesondere dann, wenn die Spannungs-/Dehnungskurve eine höhere Biegung aufweist.
- Pulldown-Menü Ordnung Volumenmodul: Wählen Sie die Ordnung der Volumenmodulberechnung für die Kurvenanpassungsroutine. Eine höhere Ordnung führt zu einer genaueren Anpassung an die Testdaten. Einige Materialmodelle können diesen Wert nicht schätzen, es sei denn, die volumetrischen Testdaten werden bereitgestellt. Andere Materialmodelle setzen diesen Eintrag standardmäßig auf 1-Konstante, es sei denn, die volumetrischen Testdaten werden in der Kurvenanpassung eingegeben und verwendet.
- Schaltfläche Kurvenanpassung ausführen: Klicken Sie auf diese Schaltfläche, um mit der Kurvenanpassung zu beginnen. Das Dialogfeld Kurvenanpassungsprozess wird eingeblendet. Klicken Sie anschließend auf die Schaltfläche Anpassen, um den iterativen Prozess zu starten. Wenn der Befehl erfolgreich durchgeführt wurde, wird die Genauigkeit der Kurvenanpassung angegeben (Effektivwert); kleinere Werte zeigen eine präzisere Anpassung an die ausgewählten Daten an. Wenn der Befehl nicht erfolgreich ist, ändern Sie die anfänglichen Schätzungen auf der Registerkarte Parameter und versuchen Sie erneut, die Kurvenanpassung auszuführen. Anmerkung: Die Kurvenanpassung verwendet verschiedene Annäherungs-Anpassungsalgorithmen zum Ermitteln der Materialkonstanten. Deshalb können verschiedene numerische Techniken und Eingabeparameter zu verschiedenen Lösungen führen. Eine Feinabstimmung der Werte kann zu einer anderen Kurvenanpassung führen. Da die Testdaten Abweichungen aufgrund unkontrollierbarer Faktoren enthält, sind Unterschiede in der Kurvenanpassungsroutine in der Regel zu vernachlässigen. (Weitere Informationen zu Kurvenanpassungsmethoden finden Sie in den Lehrbüchern Numerische Methoden oder auf den entsprechenden Webseiten .)
Abschnitt Ergebnisse des Kurvenanpassungsschemas
Die von der Kurvenanpassung berechneten Materialmodellkonstanten werden in diesem Abschnitt beschrieben. Um die Wirkung zu sehen, die die Konstanten auf die Daten haben, ändern Sie einen Wert und wählen Sie einen Typ der dargestellten Daten zum Aktualisieren des Diagramms.
Diese Werte werden aus dem Fenster Kurvenanpassung Materialdaten in das Fenster Elementenmaterial angeben kopiert, wenn Sie auf die Schaltfläche OK zum Schließen des Fensters Kurvenanpassung Materialdaten klicken.
Die folgenden Gleichungen werden für die verschiedenen Materialmodelle verwendet:
- Neo-Hookean
- Uniaxial: Tu = Spannung = 2(λu - λu2)C10, wobei I1 = λu2 + 2λu-1
- Äquibiaxial: TB = Spannung = 2(λB - λB-5)C10, wobei I1 = 2λB2 + λB-4
- Reine Scherung: TS = Spannung = 2(λS - λS-3)C10, wobei I1 = λS2 + 1 + λS-2
- Volumetrisch: p = Druck = -K(J-1), wobei J = λv3
wobei λ = Ausdehnung = 1 + Dehnung
- Van der Waals:
- Uniaxial: wobei I1 =λu2 + 2λu-1 und I2 =λu-2+ 2λu
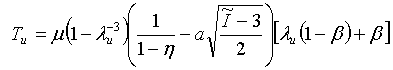
- Äquibiaxial: wobei I1 = 2λB2 + λB-4 und I2 = 2λB-2+ λB4
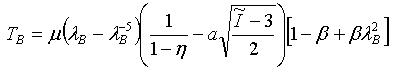
- Reine Scherung: wobei I1 =λS2 + 1 + λS-2 und I2 =λS2+ 1 + λS-2
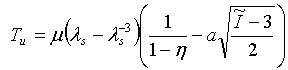
- Volumetrisch: p = Druck = -0.5K(J-1/J), wobei J = λv3, wobei
- Uniaxial:
![]()
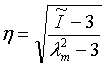
- Yeoh:
- Uniaxial: wobei I1 =λu2 + 2λu-1
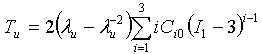
- Äquibiaxial: wobei I1 = 2λB2 + λB-4
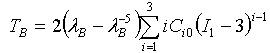
- Reine Scherung: wobei I1 =λS2 + 1 + λS-2
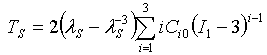
- Volumetrisch: wobei J = λv3
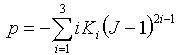
- Uniaxial:
Abschnitt Vergleich der Eingabedaten für zugeschnittene Kurven
In diesem Abschnitt werden die tabellarischen Testdaten und die angepasste Kurve dargestellt. Verwenden Sie die Dropdown-Liste Typ der dargestellten Daten, um auszuwählen, was im Diagramm angezeigt werden soll. Jeder Typ, für den Daten eingegeben werden, kann unabhängig davon angezeigt werden, ob diese Daten in der Kurvenanpassung verwendet werden oder nicht. (Daten, die in der Kurvenanpassungsroutine nicht verwendet werden, weisen wahrscheinlich keine Konstanten auf, die gut zu den Daten passen. Die angepasste Kurve folgt wahrscheinlich den Tabellendaten nicht sehr gut.)
Das Diagramm wird nicht automatisch aktualisiert, wenn die Materialmodellkonstanten manuell geändert werden. Um das Diagramm zu aktualisieren, wählen Sie den Typ der dargestellten Daten aus.
Beispiel für eine Kurvenanpassung
Führen wir ein Beispiel mit einfachen Spannungsdaten, äquibiaxial, und reinen Scherungsdaten mit einem Ogden-Materialmodell aus.
- Legen Sie ein Modell mit Ziegel- oder 2D-Elementen auf die Analyseart Nichtlinear fest (entweder Statische Spannung mit nichtlinearen Materialmodellen oder MES mit nichtlinearen Materialmodellen). Die Testdaten werden in MPA angegeben, sodass die Modelleinheiten Newton und Millimeter sein sollten. (1 MPa = 1 N/mm ^ 2)
- Bearbeiten Sie die Elementdefinition. Klicken Sie mit der rechten Maustaste auf Elementdefinition für das Bauteil, und wählen Sie die Option Elementdefinition bearbeiten. Legen Sie das Materialmodell auf Hyperelastisch: Ogden fest. Klicken Sie auf OK.
- Bearbeiten Sie die Materialeigenschaften. Klicken Sie mit der rechten Maustaste auf Material für das Bauteil, und wählen Sie Material bearbeiten. Wählen Sie [Anwenderdefiniert], und klicken Sie auf die Schaltfläche Eigenschaften bearbeiten. Falls die Ogden-Materialkonstanten bekannt sind, können sie direkt eingegeben werden. Da die Materialtestdaten (unten angegeben) vorliegen, klicken Sie auf die Schaltfläche Kurvenanpassung.
- Klicken Sie zum Eingeben der Spannungs-/Dehnungstestdaten der einfachen Spannung auf die Schaltfläche Einfache Spannung. Fügen Sie entweder Zeilen in der Tabelle ein, und geben Sie die unten angegebenen Daten ein, oder kopieren Sie den unten aufgeführten Text und fügen ihn in eine Textdatei (.csv) ein. Verwenden Sie Importieren, um die Daten einzulesen. Klicken Sie auf OK, wenn Sie fertig sind.
- Geben Sie die gleichen biaxialen Spannungs-/Dehnungstestdaten auf ähnliche Weise ein. Klicken Sie auf die Schaltfläche Äquibiaxial. Fügen Sie entweder Zeilen in der Tabelle ein, und geben Sie die unten angegebenen Daten ein, oder kopieren Sie den unten aufgeführten Text und fügen ihn in eine Textdatei (.csv) ein. Verwenden Sie Importieren , um die Daten einzulesen. Klicken Sie auf OK, wenn Sie fertig sind.
- Geben Sie die Testdaten für reine Scherung und Spannung-Dehnung auf eine ähnliche Weise ein. Klicken Sie auf die Schaltfläche OK. Fügen Sie entweder Zeilen in der Tabelle ein, und geben Sie die unten angegebenen Daten ein, oder kopieren Sie den unten aufgeführten Text und fügen ihn in eine Textdatei (.csv) ein. Verwenden Sie Importieren , um die Daten einzulesen. Klicken Sie auf OK, wenn Sie fertig sind.
- Aktivieren Sie auf der Registerkarte Steuerung das Kontrollkästchen für die einzelnen Testdaten.
- Für das Ogden-Materialmodell sind Kurvenanpassungsmethode und Teilweise lineare Annäherung ein guter Ausgangspunkt, da eine Schätzung für nur einen der Parameter (der Alpha-Wert) erforderlich ist. Wählen Sie diese Methode also aus dem Pulldown-Menü aus. Übernehmen Sie für die anderen Einstellungen die Vorgaben. Beachten Sie, dass Ordnung Volumenmodul abgeblendet ist, da keine volumetrischen Daten angegeben wurden.
- Legen Sie auf der Registerkarte Parameter den Wert Geschätztes Alpha, den Bereichswert und das Inkrement wie folgt fest. Dadurch erhalten Sie einen mäßig breiten Bereich von Werten für die zu verwendende Lösung. Ein Inkrement von 20 ist eine grobe, jedoch gute Annäherung für die erste Ausführung, ohne dass es zu lange dauert, um alle Permutationen zu berechnen. Beachten Sie, dass die Schätzwerte die Standardwerte für das Ogden-Materialmodell sind.
Ordnung Geschätztes Alpha Bereichswert Inkrement 1 1.2 10 20 2 -2 10 20 3 6 10 20 - Klicken Sie auf der Registerkarte Steuerung auf die Schaltfläche Kurvenanpassung durchführen und dann auf die Schaltfläche Anpassen. Der Effektivwert-Fehler beträgt 0.184: relativ groß im Vergleich zur maximalen Spannung. Klicken Sie auf die Schaltfläche OK.
- Mithilfe des Pulldown-Menüs Typ der dargestellten Daten überprüfen Sie das Diagramm für jede der Kurvenanpassungsdaten (einfache Spannung, äquibiaxial und reine Scherung). Die Kurven folgen den Testdaten recht gut (Äquibiaxial ist die meiste Zeit deaktiviert), sodass die ermittelten Konstanten die richtige Größenordnung aufweisen.
- Ändern Sie bei einer guten Schätzung die Kurvenanpassungsmethode in Levenberg-Marquardt-Algorithmus. Geben Sie die geschätzten Werte auf der Registerkarte Parameter mithilfe der zuvor gefundenen Lösung ein. Da für die Schätzwerte keine Genauigkeit erforderlich ist, genügen die folgenden abgerundeten Werte:
Ordnung Geschätzte Mu Geschätztes Alpha 1 -0.16 6.2 2 4.4 0.5 3 0.026 9 - Klicken Sie auf die Registerkarte Steuerung, klicken Sie auf die Schaltfläche Kurvenanpassung durchführen, und klicken Sie dann auf die Schaltfläche Anpassen. Der Effektivwert-Fehler beträgt 0.183: kaum besser als die vorherige Anpassung. Beachten Sie, wie diese Lösungsmethode viel schneller als die teilweise lineare Annäherungsmethode ist.
- Zusätzliche Testversionen können mithilfe verschiedener ursprünglicher Werte durchgeführt werden, um alternative Mindestwerte zu ermitteln. Es ist jedoch produktiver, ein Modell höherer Ordnung zu testen. Klicken Sie auf die Registerkarte Steuerung. Legen Sie Ordnung des Modells auf 5 fest und die Kurvenanpassungsmethode auf Teilweise lineare Annäherung. Klicken Sie auf die Registerkarte Parameter, und geben Sie Schätzwerte wie folgt ein. Zwei Anmerkungen. Erstens: Da die Ordnung des Modells geändert wurde, sind die mit der vorherigen Lösung ermittelten Konstanten in der Regel keine relevanten Schätzungen in einem effizienteren Lösungsalgorithmus wie Levenberg-Marquardt. Es empfiehlt sich in diesem Fall, mit der teilweisen linearen Annäherung zu beginnen. Zweitens: Beachten Sie, dass der Inkrementwert im Vergleich zu zuvor reduziert wurde. Da die Berechnung jede Kombination von Alpha der ersten Ordnung mit jeder Kombination von Alpha der zweiten Ordnung usw. durchführt, kann eine Lösung der fünften Ordnung viele Berechnungen schnell erstellen. Der kleinere Inkrementwert wird verwendet, um die Zeit der Kurvenanpassungsroutine zu minimieren.
Ordnung Geschätztes Alpha Bereichswert Inkrement 1 1.2 10 10 2 -2 10 10 3 6 10 10 4 19 10 10 5 1 10 10 - Klicken Sie auf die Registerkarte Steuerung, klicken Sie auf die Schaltfläche Kurvenanpassung durchführen, und klicken Sie dann auf die Schaltfläche Anpassen. Der Effektivwert-Fehler beträgt 0.142. Wie erwartet, passt jede Kurve unter Typ der dargestellten Daten besser zu den Testdaten. Die Ergebnisse werden in Abbildung 1 dargestellt. Zusätzliche Testversionen könnten ausgeführt werden, aber aufgrund der Genauigkeit der Testdaten sollte diese Kurvenanpassung annehmbar sein.
Testdaten für einfache Spannung
0,0
0.02,0.08
0.06,0.12
0.28,0.30
0.47,0.4
0.67,0.57
0.77,0.7
0.82,0.78
0.85, 0.9
0.89, 1.0
Äquibiaxiale Testdaten
0,0
0.02,0.14
0.06,0.25
0.12,0.4
0.28,0.6
0.43,0.8
0.57,0.95
0.65,1.16
0.72,1.4
0.80,1.72
0.89,2.4
Testdaten für reine Scherung
0,0
0.02,0.08
0.07,0.2
0.20,0.37
0.59,0.71
0.73,0.92
0.83,1.1
0.89,1.28