Mehrpunktabhängigkeiten (MPCs) sind eine erweiterte Funktion, mit der Sie verschiedene Knoten und Freiheitsgrade in der Analyse miteinander verbinden. Sie werden häufig verwendet, um einen Randbedingungseffekt zu simulieren, wenn normale Randbedingungen nicht zum richtigen Verhalten führen.
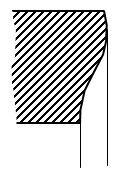
Eine der Einsatzmöglichkeiten für MPCs ist eine Master- und Slave-Situation: die Verschiebung an Knoten X (Slave) muss die Gleiche wie am Knoten Y (Master) sein. In Abbildung 1 ist ein Teil eines langen Behälters modelliert. Die linken Seite verwendet Symmetrie-Randbedingungen; dies beschränkt das Modell in der Z-Verschiebung und simuliert den Teil des Tanks auf der linken Seite. Für einen langen Behälter zwingt der Teil des Tanks auf der rechten Seite des Modells diese Knoten, in einer Ebene zu bleiben. Eine Symmetrie-Randbedingung funktioniert, mit der Ausnahme, dass diese kein axiales Wachsen oder Schrumpfen im Tank verhindern. Stattdessen werden MPCs verwendet, um anzugeben, dass die Z-Verschiebung aller Knoten gleich ist (jedoch nicht unbedingt 0). Auf ähnliche Weise können Temperaturen in einer thermischen Berechnung und Spannungen bei elektrostatischen Analysen die Grundlage von MPCs sein.
|
Detail: |
|||
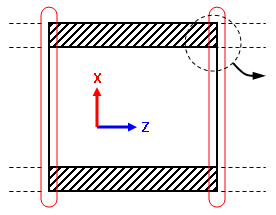
| Z-Symmetriebedingungen schränken die linke Fläche ein. Diese Knoten verschieben sich nicht in Z-Richtung. | MPC-Bedingungen beschränken die rechte Fläche auf eine Ebene; der Knoten verschiebt sich gemeinsam in Z-Richtung. | Ohne MPC oder andere Randbedingungen können die Knoten auf der rechten Fläche aufgrund der Lasten abgelenkt werden. Dies simuliert nicht genau den Teil des Behälters, der nicht in die Analyse eingeschlossen ist. | ||
| Abbildung 1: Verwenden von Mehrpunktabhängigkeiten | ||||
Die Eingabe für Mehrpunktabhängigkeiten ist eine Gleichung im folgenden Format:
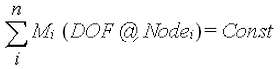
Dabei gilt:
- i ist der i-te Term der Gleichung
- M i ist ein Multiplikator für Term i der Gleichung
- DOF@Node i ist ein Freiheitsgrad (FHG) an einem bestimmten Knoten für Term i. Der FHG-Typ ist vom Analysetyp abhängig (translatorische oder rotatorische Verschiebungen für lineare Strukturanalysen, Temperatur für thermische Analysen und Spannung für elektrostatische Analysen).
- n steht für die Anzahl von Termen in der Gleichung
- Const ist die Konstante, der die Gleichung entspricht. Dieser Wert ist häufig Null.
Wenn die Gleichung Einheiten umfasst, werden diese unter Verwendung der Modelleinheiten geschrieben. MPC-Gleichungen verwenden keine Anzeigeeinheiten.
Eingeben der MPC-Gleichung
- Notieren Sie im FEM-Editor die Nummern der Punkte und die zugehörigen Freiheitsgrade für die MPC-Gleichungen. Um die Nummern der Punkte zu erhalten, verwenden Sie Auswahl
Auswählen Punkte, um einen Punkt auszuwählen, klicken Sie mit der rechten Maustaste, und wählen Sie Abfragen. (Oder halten Sie den Mauszeiger über einem Punkt, um die Eigenschaften in einer QuickInfo anzuzeigen.) - Bei Analysen, auf die er angewendet werden kann, befindet sich der Befehl Mehrpunkt-Abhängigkeit auf der Registerkarte Setup der Multifunktionsleiste.
- Bei linearen Strukturanalysen befindet sich der Befehl im Pulldown-Menü der Gruppe Abhängigkeiten.
- Bei thermischen Analysen befindet sich der Befehl im Pulldown-Menü der Gruppe Thermolasten.
- Bei elektrostatischen Analysen befindet sich der Befehl im Pulldown-Menü der Gruppe Lasten.
Mehrpunktabhängigkeit auswählen. Verwenden Sie das Dialogfeld Mehrpunktabhängigkeiten definieren, um alle Terme der vorherigen Gleichung einzugeben. - Klicken Sie auf die Schaltfläche Hinzufügen, um eine neue Abhängigkeitsgleichung zu erstellen; der Name der Gleichung wird automatisch ausgefüllt. Oder verwenden Sie das Dropdown-Menü Gleichungsname, um eine vorhandene Gleichung zum Bearbeiten auszuwählen.
- Geben Sie die Konstante der Gleichung im Feld Konstante ein. (Const in der obigen Gleichung.)
- Verwenden Sie die Schaltfläche Zeile hinzufügen, um so viele Zeilen wie erforderlich in die Tabellenkalkulation einzufügen, um jeden Term der Gleichung anzugeben. Geben Sie in jeder Zeile den Multiplikator und die Knoten-ID (die Knotennummer, die Sie in Schritt 2 notiert haben) sowie den entsprechenden Freiheitsgrad ein. Verwenden Sie die Dropdown-Liste für lineare Analysen. Der Freiheitsgrad ist für thermische und elektrostatische Analysen fest (FHG = Temperatur bzw. Spannung ). Anmerkung: Wenn ein Punkt einem lokalen Koordinatensystem zugewiesen ist, befindet sich der ausgewählte Freiheitsgrad ebenfalls im lokalen Koordinatensystem. Beispiel: Die X-Verschiebung bezieht sich auf die radiale Verschiebungsrichtung in einem zylindrischen Koordinatensystem, Y-Verschiebung bezieht sich auf die tangentiale Richtung und so weiter.
- Wählen Sie die Lösungsmethode, und legen Sie die Pönale fest (die Pönale wird für die Strafmethode verwendet). Wählen Sie eine der folgenden Lösungsmethoden:
- Automatisch
- Strafbasierende Methode
- Kondensierungsmethode
Anmerkung: Sie finden die empfohlenen Werte für die Pönale in den jeweiligen Hilfethemen zur Einrichtung. Suchen Sie nach "Pönale", um schnellen Zugriff auf die Hilfethemen zu erhalten.Anmerkung: Die von Ihnen im Dialogfeld Mehrpunktabhängigkeiten definieren gewählte Lösungsmethode wird als Methode für alle Elemente mit Mehrpunkt-Abhängigkeiten festgelegt. Dazu gehören unter anderem zyklische Symmetrie, reibungslose Abhängigkeiten, die intelligente Verklebung und benutzerdefinierte Mehrpunkt-Abhängigkeiten. Wenn Sie beispielsweise die Methode Über Lösungsabweichung verwenden möchten, um alle Analysen mit intelligenter Verklebung zu lösen, können Sie die standardmäßige Kondensierungsmethode überschreiben, indem Sie im Dialogfeld Mehrpunktabhängigkeiten definieren die Option Über Lösungsabweichung auswählen. - Klicken Sie auf die Schaltfläche OK, um das Dialogfeld zu schließen.
- Führen Sie die Analyse durch.
Kompatibilitätsanmerkung: Version 20 bis 20.4 SP1
Die in Version 20 bis 20.4 SP1 verwendete Eingabe zum Speichern der MPC-Daten ist nicht mehr kompatibel. Um die ursprünglichen Eingaben wiederherzustellen, bearbeiten Sie die Datei DS.CST.BAK im Entwurfsszenario-Ordner (z. B. Modellname.ds_data\1). Dadurch erhalten Sie die ursprünglichen MPC-Gleichungen. Die Knotennummern müssen in die entsprechenden Punktnummern konvertiert werden und dann müssen die Gleichungen über Hinzufügen Mehrpunktabhängigkeit erneut eingegeben werden. Die .CST.BAK-Datei hat folgendes Format:
| #_equations, max_n | Zwei Zahlen: die Anzahl der Gleichungen in der Datei (#_equations) und die maximale Anzahl von Termen in den Gleichungen (max_n, ohne die Konstante, der die Gleichung entspricht). Beide Zahlen müssen Ganzzahlen sein. |
| #_terms(1) | Anzahl der Terme in Gleichung 1. Dies muss eine Ganzzahl sein. |
|
node(1), DOF(1), M(1) node(2), DOF(2), M(2) node(3), DOF(3), M(3) node(#_terms), DOF(#_terms), M(#_terms) |
Drei Ziffern pro Zeile und #_terms Zeilen von Zahlen. Die drei Werte sind die Knotennummer (node(i)), der Freiheitsgrad an den Knoten (DOF(i)) und der Multiplikator für den Term (M(i)). Der Multiplikator muss eine reelle Zahl und die beiden anderen müssen eine Ganzzahl sein. Die gültigen Werte für DOF(i) sind wie folgt: 1 = X-Verschiebung 2 = Y-Verschiebung 3 = Z-Verschiebung 4 = X-Drehung 5 = Y-Drehung 6 = Z-Drehung |
| Constant(1) | Der konstante Wert für Gleichung 1. Diese Zahl muss eine reelle Zahl sein. (1.00 oder 1.0E0 statt 1) |
| Die obigen drei Zeilen [#_terms; node(i), DOF(i), M(i); Constant] wiederholen sich für jede MPC-Gleichung, Nummer 2 bis #_equations. |
Beispiel
Analysieren Sie den Zahnradzug in Abbildung 2. Statt zu versuchen, die Zahnräder mit Balkenelementen zu modellieren, um die Drehverbindung zu simulieren, verwenden Sie Mehrpunktabhängigkeiten. Für die Zahnräder gilt: Radius1*Drehung1 = -Radius2*Drehung2. Daher lautet die MPC-Gleichung: Radius1*Drehung1 + Radius2*Drehung2 = 0. Für die gegebenen Bemaßungen und Punktnummern lautet die Eingabe für MPC wie folgt:
Gleichung 1
Konstante = 0
| Multiplikator | Punkt-ID | Freiheitsgrad |
|---|---|---|
| 3 | 12 | X-Drehung |
| 9 | 18 | X-Drehung |
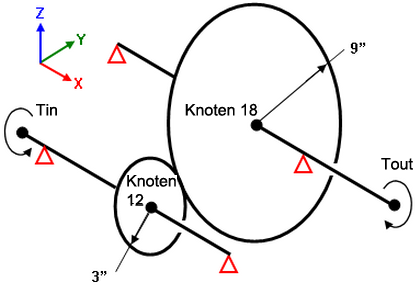
Abbildung 2: Zahnradzug analysiert mit Balkenelementen