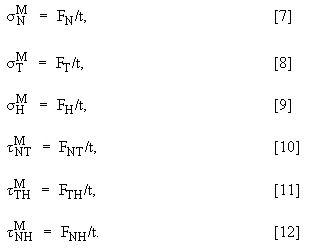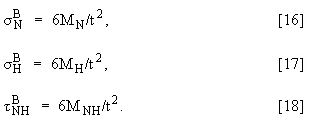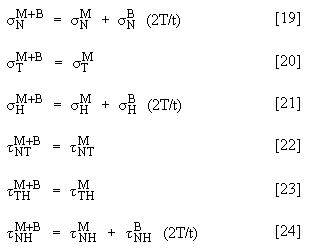Auf dieser Seite wird beschrieben, wie die primäre Membran- und die primäre Biegespannung (Pm und Pb) berechnet werden.
Die Berechnung dieser Spannungen umfasst mehrere Schritte. Beginnen Sie mit der Umformung der sechs globalen Spannungstensoren im lokalen Koordinatensystem, festgelegt durch die Spannungsklassifizierungslinie SKL (Stress Classification Line, SCL). Sie fahren mit der Integration der sechs Spannungstensoren σN, σT, σH, τNT, τTH, τNH entlang der SKL fort, um die Gesamtlast zu erhalten (FN,T, FH, FNT, FTH, FHN), indem Folgendes verwendet wird:
T ist die Position entlang der SKL.
Anschließend wird die Membranspannung (F/A) für alle 6 Komponenten berechnet. Für eine SKL der Länge t:
Die wichtigsten Membranspannungen (
) werden aus dem Tensor abgeleitet, dessen Komponenten durch die Gleichungen 7 bis 12 gegeben sind. Diese Spannungen werden ermittelt, indem dieser Tensor in Hauptachsenrichtung umgeformt wird.
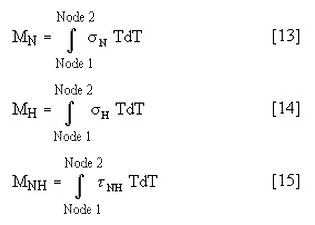
Im nächsten Schritt werden die Biegespannungen durch Subtrahieren der Membranspannung von der gesamten Lastverteilung ermittelt. Dies erfolgt von Spannungspunkt zu Spannungspunkt. Im ersten Schritt wird die Verteilung der Momentlast für die SKL der Länge t ermittelt. Dann wird die Verteilung der Momentlast integriert, um das Moment auf dem Querschnitt zu bestimmen.
Diese Integrale sollten mit der Trapezintegration berechnet werden. Die nachfolgenden Ergebnisse werden zur Berechnung der Biegespannung (Mc/I) für die SKL der Länge t mit folgenden Formeln verwendet:
Im nächsten Schritt wird die Hauptspannung an jedem Ende der SKL (
) berechnet. Die Hauptmembranspannung und Hauptbiegespannung werden aus dem Tensor abgeleitet, dessen Komponenten durch Ersetzen von T = Knoten 1 und T = Knoten 2 abgeleitet werden.
Die Membranspannungen werden durch die Gleichungen 7 bis 12 und die Biegespannung durch die Gleichungen 16 bis 18 ermittelt. Achten Sie darauf, wie zwei Sätze von Hauptspannungen abgerufen werden: einer bei T = Knoten 1 und ein anderer bei T = Knoten 2. Die Hauptspannungen werden ermittelt, indem der Tensor wieder in Hauptachsenrichtung umgeformt wird.
Nunmehr liegen alle Hauptmembranspannungen,
sowie die Summe der Hauptmembran- und Hauptbiegespannungen vor:
Diese Werte sind zur Bestimmung der Ausgabeskalargrößen erforderlich:
- Pm und
- Pm + Pb
Diese zwei Skalarwerte werden basierend auf zwei verschiedenen Kombinationsmethoden berechnet und ausgegeben: maximale Scherspannung und Von-Mises-Spannung. Die folgende Tabelle listet die Gleichungen auf, die für jeden Wert und jede Berechnungsmethode verwendet werden:
| Tabelle 1: Pm und (Pm + Pb) Gleichungen für jede Berechnungsmethode | |||
|---|---|---|---|
| Max. Scherspannung (Methode) | Von Mises-Spannung (Methode) | ||
Pm = Größter Wert von  |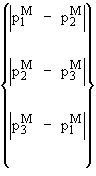
[25] |
|
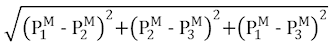
[27] |
(Pm + Pb) = Größter Wert von  |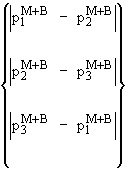
[26] * |
|
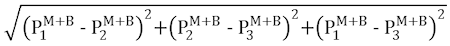
[28] * |
* Anmerkung: Die Gleichungen 26 und 28 müssen zweimal ausgewertet werden, da zwei Gruppen von Werten vorhanden sind: eine bei T = Knoten 1 und eine andere bei T = Knoten 2. Die Ausgabegröße basiert auf dem Knoten mit dem größten resultierenden Wert.
Zum Abschluss wird die Intensität der primären Biegespannung (Pb) mit der folgenden einfachen Differenzengleichung für beide Spannungskombinationsmethoden berechnet:
Pb = (Pm + Pb) - Pm[29]
Literatur: ASME SGDA-99-2, PROPOSED NON-MANDATORY APPENDIX for Subcommittees III & VIII, Interpretation of Finite Element Analysis Stress Results, Rev 4, 2000.