Das Materialmodell für armierten Beton wird als statistisch homogen mit unterschiedlichem Zug- und Druckverhalten behandelt. Es folgt einem verschmierten Rissmodell, in dem Reißen und Brechen als Degeneration der Elastizität an Integrationspunkten simuliert werden, statt einzelne makroskopische Risse zu verfolgen. Das hier beschriebenen Modell ist für relativ monotone Belastungen vorgesehen. (Eine echt monotone Last wird entweder erhöht oder verringert, aber nicht rückgängig gemacht.) Im aktuellen Modell ist Rissbildung der wichtigste Aspekt, aber auch Druck unter Einschränkung wird angemessen berücksichtigt.
Das Materialmodell für armierten Beton implementiert auch einen Ansatz der verschmierten Armierung. Es wird angenommen, dass die Armierung über das ganze Element mit einem bestimmten Volumenanteil verteilt (verschmiert) wird. Die Stärke der Armierung verstärkt den Beton in der angegebenen Richtung. Das Armierungsmaterial selbst folgt einem elastoplastischen Materialmodell mit von Mises mit isotroper Verhärtung. Drei unabhängige Richtungen der Armierungen können definiert werden.
Abbildung 1 zeigt ein typisches uniaxiales Verhalten von einfachem Beton. Wenn Beton unter Druck belastet wird (Punkte 3-2-1), verhält er sich elastisch bis zum Gleitpunkt (Punkt 2). Die Materialantwort wird erweicht, und nicht wiederherstellbare Verformung erfolgt. Nach Erreichen des Fehlerpunkts an der höchsten Stärke (Punkt 1) verschlechtert sich das Material, kann jedoch trotzdem theoretisch noch einige Lasten tragen. Diese Druckerweichung wird derzeit in der Analyse nicht modelliert, und der Beton wird nach diesem Punkt als gebrochen und unfähig zum Tragen jeglicher Last betrachtet. Die Entlastung vor dem Fehler wird als elastisch angenommen und folgt dem Elastizitätsmodul.
Wenn Beton unter Spannung belastet wird, verhält er sich elastisch, bis er die Fehlerstärke erreicht (Punkt 4). Das Verhalten nach dem Fehler unter Spannung (Spannungserweichung) ist bei der Modellierung von Lasttranser über Risse (Spannungsversteifung) in armiertem Beton sehr wichtig.
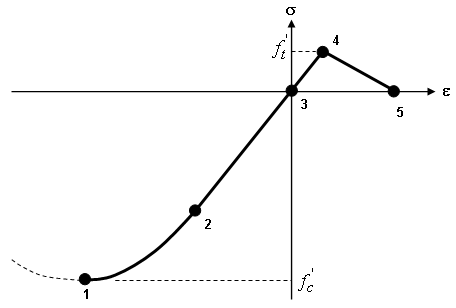
Abbildung 1: Idealisiertes uniaxiales Verhalten von einfachen Beton
Fehlerkriterium
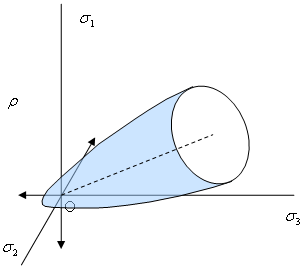
Es empfiehlt sich, im Hauptspannungsbereich zu arbeiten, in dem alle Spannungszustände durch die Haigh-Westergaard-Koordinate (x, r, q) definiert sind:
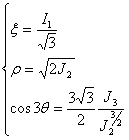(1)
wobei I1=δijσij, J2=0.5SijSij, J3=(SijSjkSki)/3, and Sij=σij - (δijσkk)/3.
|
(a) Hauptspannungsbereich |
|
(b) Deviatorische Ebene mit daraufprojizierter Hauptspannung |
| Abbildung 2: Haigh-Westergaard-Spannungskoordinaten |
In der Analyse wird ein ähnliches Fehlerkriterium wie das Vier-Parameter-Kriterium von Hsieh-Ting-Chen (HTC) verwendet (Referenz 1). Die Auswirkung der Abhängigkeit wird jedoch über die deviatorische Radiusdarstellung von Willam und Warnke eingeführt (Referenz 2).
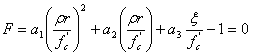(2)
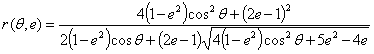(3)
wobei ft' und fc' die uniaxiale Zug- bzw. Drucksfestigkeit (absolute Werte) sind und e die gemäß Kang und Willam definierte Exzentrizität ist:
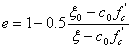(4)
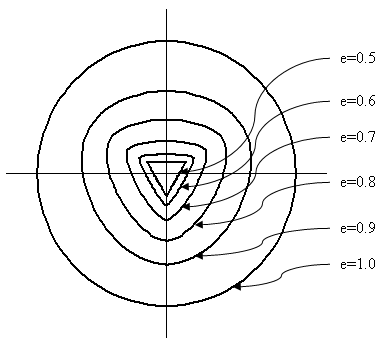
wobei c 0 eine Materialkonstante ist, die nach Experimenten kalibriert werden kann (bei Kang und Willam ist sie auf 5,5 festgesetzt, Referenz 5). Die äqui-triaxiale Zugfestigkeit ζ 0 =sqrt(3)f t '. Die Exzentrizität 1 ist ein Kreis in der deviatorischen Ebene (Abbildung 3), und der Fehler ist dann unabhängig vom Lode-Winkel ϑ.
Das Belasten der Streckfläche wird als Erweiterung der anfänglichen Streckfläche auf die endgültige Fehlerfläche über einen einzigen Parameter k angenommen, dessen Wert im Bereich von k 0 bei der anfänglichen Streckung bis 1 beim Fehler liegt. Gemäß Imran und Pantazopoulou (Referenz 4) wird der Schnittpunkt der dazwischen Liegenden Fehlerflächen mit der hydrostatischen Achse durch einen weiteren Term gesteuert.
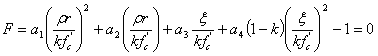(5)
Außerdem wird in der Analyse von keiner Streckung für den zugdominanten Status ausgegangen, indem eine Zuggrenze eingeführt wird (maximale Zugfestigkeit, bzw. das Rankine-Kriterium). Im gemischten Zug-Druck-Bereich (Referenz 1) bilden sich die Streckflächen allmählich heraus. Die Bruchlinie ist somit eine offene Fläche im Hauptspannungsbereich, wie in Abbildung 3 gezeigt. Bei der Analyse wird immer davon ausgegangen, dass der Fehler ein Riss ist, wenn eine Hauptzugspannung vorliegt. Dies ist etwas willkürlich, da Beton auf komplizierte Weise versagen kann. Infolgedessen unterscheiden einige Untersuchungen nicht nach Fehlertypen.
|
(a) Betonbruchlinie |
|
(b) Deviatorische Ansicht der Bruchlinie |
| Abbildung 3: Bruchlinie |
Druckverfestigung
Der Einfachheit halber wird die zugehörige Strömungs- und isotrope Dehnungsverfestigung verwendet, wenn Beton hauptsächlich unter Druckbelastung steht. Diese Methode führt zu symmetrischen zugrunde liegenden Gleichungen und ist berechnungseffizient. Sie überschätzt jedoch in der Regel die plastische Volumendehnung.
In der gemischten Zug- und Druckdomäne (Referenz 1) wird die Streckfläche geändert und zur tangentialen Fläche zum Ursprung an der Grenze (siehe Abbildung 4).
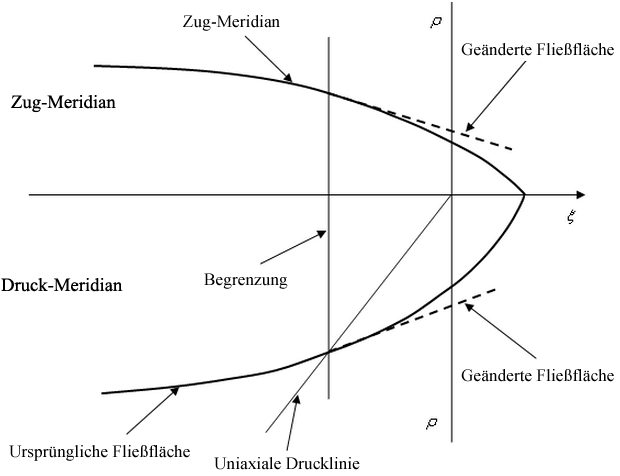
Abbildung 4: Streckfläche in gemischter
Die Spannungsaktualisierung erfolgt durch das voll implizite Rückwärts-Euler-Verfahren, für das Berechnungen von erheblichem Umfang erforderlich sind.
Zugversteifung
Es wird angenommen, dass Rissbildung auftritt, wenn mindestens eine Hauptspannung an der Fehlerfläche eine Zugspannung ist. In der Analyse wird beschädigte Elastizität zum Modellieren des gerissenen Betons verwendet. Es wird davon ausgegangen, dass keine dauerhafte Dehnung mit den Rissen zusammenhängt.
Um die Netzempfindlichkeit im Zusammenhang mit der Zugerweichung zu überwinden, wird in der Analyse angenommen, dass die Bruchenergie (pro Flächeneinheit) Gf eine Materialeigenschaft ist. Die spezifische Bruchenergie (pro Volumeneinheit), gf hängt mit Gf wie folgt zusammen:
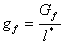(6)
Dabei ist l* die charakteristische Länge oder Rissbandbreite an den Integrationspunkten (Referenz 6).
Der Schubrückhaltungskoeffizient b wird vom Benutzer angegeben. Ein Wert von 1 steht für einen vollkommen rauen Riss, in dem die Schubkraft ohne Verlust übertragen werden kann. Der Wert 0 steht für einen vollkommen glatten Riss, in dem keine Schubkraft übertragen werden kann. Der Poisson-Effekt (Querdehnung) im Zusammenhang mit der Rissbildung wird vernachlässigt. Wenn der Riss sich schließt, kann die Druckspannung vollständig übertragen werden.
Spannungskomponenten, die einem offenen Riss zugeordnet sind, sind in der Definition der Fehlerfläche zum Feststellen weiterer Risse am gleichen Integrationspunkt nicht eingeschlossen.
Berechnen von Bruchlinien
Wie oben angegeben (Gleichung 2, mit ρ=0), wird a3 aus einem äqui-triaxialen Zustand ermittelt. Andere Fehlerflächenparameter (a1, a2 und c0) werden anhand von nichtlinearen Gleichungen (Gleichungen 2, 3 und 4) in drei unabhängigen Spannungszuständen gelöst. Für andere Kombinationen von Experimenten muss der Benutzer die Parameter berechnen und dann direkt eingeben.
Für die Verfestigungsparameter (a4 und k0) wird in der Analyse davon ausgegangen, dass eine ungleichmäßige Arbeitsverfestigung gemäß dem zusätzlichen Verfestigungsterm (Gleichung 5) vorliegt. Der Einfachheit halber wird angenommen, dass die Abhängigkeit der Verfestigung von der effektiven plastischen Dehnung (
) und dem hydrostatischen Druck (ζ) trennbar ist. Die effektive plastische Dehnung () betrifft nur den Verfestigungsparameter k. Daher können die Benutzer a4 und k() basierend auf dem uniaxialen Druckexperiment kalibrieren.
Referenzen
- Chen, W.F. und Han, D.J., Plasticity for structural engineers, Springer, 1998
- Willam, K. und Warnke, E., Constitutive model for triaxial behavior of concrete. Internationale Vereinigung für Brücken- und Hochbau, Zürich, S.1-30, 1975
- Kupfer, H. und Gerstle, K., Behavior of concrete under biaxial stresses, Journal of Engineering Mechanics, v99, n4, S. 853-866, 1973
- Imran I. und Pantazopoulou S., Plasticity model for concrete under triaxial compression. Journal of Engineering Mechanics, v127, n3, S. 281-290, 2001
- Kang, H. und Willam, K., Localization characteristics of triaxial concrete model, Journal of Engineering Mechanics, v125, n8, S. 941-950, 1999
- Crisfield, M.A., Non-linear finite element analysis of solids and structures, Vol. 2: Advanced topics, J. Wiley & Sons, New York, 1997