Das Materialmodell für armierten Beton wird als statistisch homogen mit unterschiedlichem Zug- und Druckverhalten behandelt. Es folgt einem verschmierten Rissmodell, in dem Reißen und Brechen als Degeneration der Elastizität an Integrationspunkten simuliert werden, statt einzelne makrosopische Risse zu verfolgen. (Risse können in bis zu drei unterschiedlichen orthogonalen Ebenen an jedem Integrationspunkt jedes Elements auftreten. Die Anzahl der Integrationspunkte wird in der Elementdefinition festgelegt.) Das hier beschriebenen Modell ist für relativ monotone Belastungen vorgesehen. (Eine echt monotone Last wird entweder erhöht oder verringert, aber nicht rückgängig gemacht.) Im aktuellen Modell ist Rissbildung der wichtigste Aspekt, aber auch Druck unter Einschränkung wird angemessen berücksichtigt. Siehe Abbildung 1.
Das Materialmodell für armierten Beton implementiert auch einen Ansatz der verschmierten Armierung. Es wird angenommen, dass die Armierung über das ganze Element mit einem bestimmten Volumenanteil verteilt (verschmiert) wird. Die Stärke der Armierung verstärkt den Beton in der angegebenen Richtung. Das Armierungsmaterial selbst folgt einem elastoplastischen Materialmodell mit von Mises mit isotroper Verhärtung. Drei unabhängige Richtungen der Armierungen können definiert werden.
Tipp: Alternativen für den verschmierten Armierungsansatz
Der Ansatz der verschmierten Armierung ist ein übliches Berechnungsverfahren. Seine Näherung ist aber möglicherweise in manchen Situationen nicht akzeptabel. Eine der folgenden Methoden kann verwendet werden, um eine genauere Lösung zu erhalten:
- Verwenden Sie statt eines Bauteils, in dem die Armierungen über das Volumen des Bauteils verteilt werden, zwei Bauteile. Beide Bauteile sind als armierter Beton definiert. Das erste Bauteil besteht aus Beton ohne Armierung. Das zweite Bauteil belegt ein Betonvolumen um die Armierung und verwendet die verschmierte Armierungstechnik in seinem Volumen.
- Modellieren Sie den Beton als ein Bauteil ohne Armierung und die Armierung als zweites Bauteil mit Balken- oder Stabelementen. Im Idealfall sollten die Balken- oder Stabelemente mit jedem Knoten des Betons entlang der Länge der Armierung verbunden sein. Das kann einige Zusatzarbeit beim Erstellen des Netzes bedeuten, abhängig von der Anzahl und Komplexität der Armierung.
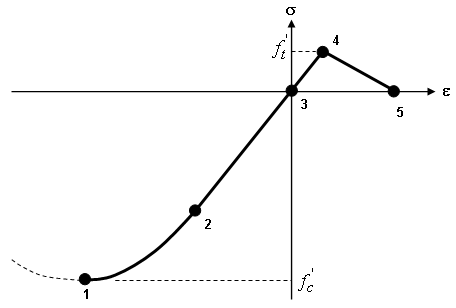
Abbildung 1: Idealisiertes uniaxiales Verhalten von einfachen Beton
Die Materialeigenschaften für armierten Beton sind Folgende. In den folgenden Beschreibungen bezieht sich einfacher Beton auf den Beton ohne Armierung. Die kombinierten Eigenschaften des Betons und der Armierung werden durch den Prozessor bestimmt.
Registerkarte Allgemein
Die Eingaben auf der Registerkarte Allgemein gelten für den einfachen Beton.
- Massendichte Geben Sie die Masse pro Volumeneinheit für den einfachen Beton (ohne Armierung) ein.
- Elastizitätsmodul Geben Sie das Elastizitätsmodul ein. Dies ist die Neigung der Spannungs-Dehnungs-Kurve eines Materials im elastischen Bereich (Punkte 2-3-4 in Abbildung 1). Es wird auch als Elastizitätsmodul bezeichnet. Dieser Wert muss größer als 0 sein.
- Poissonsche Konstante Geben Sie die Poissonsche Konstante ein. Die Querdehnung wird ermittelt, indem die negative seitliche Dehnung durch die axiale Dehnung von axial geladenen Bauteilen geteilt wird.
Registerkarte Stärke
Die Eingaben auf der Registerkarte Stärke gelten für einfachen Beton.
- Uniaxiale Zugfestigkeit Geben Sie die Stärke (Bruchspannung) des Betons abhängig von einer uniaxialen Zugfestigkeit ein (Punkt 4 in Abbildung 1). Dieser Wert muss größer als 0 sein.
- Uniaxiale Druckfestigkeit Geben Sie die Stärke (Brechspannung) des Betons abhängig von einer uniaxialen Druckfestigkeit ein (Punkt 1 in Abbildung 1). Dieser Wert wird als eine positive Zahl eingegeben und muss größer als Null sein.
- Biaxiale Druckfestigkeit Geben Sie die Stärke (Brechspannung) des Betons abhängig von äqui-biaxialen Drucklasten ein. Dieser Wert wird als ein positiver Wert oder Null eingegeben. Wenn er als Null eingegeben wird, dann bestimmt die Eingabe auf der Registerkarte Erweitert die biaxiale Druckfestigkeit.
- Zugversteifung Diese Dropdown-Liste enthält zwei Optionen zur Bildung von Rissen und den Auswirkungen auf die Stärke. Wenn Bruchenergie, linear ausgewählt wird, geben Sie den Wert für Bruchenergie/Fläche des einfachen Betons ein. Dabei handelt es sich um die Bruchenergie (zwischen dem Beginn eines Risses und dem vollständigen Versagen) pro Flächeneinheit. Ein Wert von 0 entspricht der Einstellung des Zugversteifungswerts auf Keine. Die Bruchenergie pro Volumen ist proportional zum Bereich unter der Spannungs-Dehnungs-Kurve von den Punkten 4 bis 5 (siehe Abbildung 1). Durch Multiplizieren dieses Werts mit der charakteristischen Länge ergibt sich der Wert für Bruchenergie/Fläche.
- Schubrückhaltung Wenn sich ein Riss bildet und schließt, kann das Material in der Lage sein, Schubkräfte parallel zur Ebene des Risses zu übertragen. Ein Parameter 1 gibt an, dass ein grober Riss vorliegt; dieser kann alle Schubkräfte ohne Verlust übertragen. Ein Wert von 0 gibt an, dass ein vollkommen glatter Riss ohne Reibung vorliegt; keine Schubkräfte können entlang der Rissebene übertragen werden.
Registerkarte Verhärten
Die Eingaben auf der Registerkarte Verhärten beziehen sich auf einfachen Beton. Diese Eingabe beschreibt die Spannungs-Dehnungs-Kurve des Betons unter Druck nach dem elastischen Bereich (Punkte 2 bis 1 in Abbildung 1).
Geben Sie die Werte für Dehnung und Spannung als negative Werte ein, beginnend am Gleitpunkt (Punkt 2). Mit der Schaltfläche Sortieren werden die Werte in absteigender Reihenfolge sortiert (Gleitpunkt bis Fehlerpunkt). Es sind mindestens zwei Datenpunkte erforderlich.
Die Einträge in der ersten Zeile (Index 1) stellen den Gleitpunkt dar und sind mit dem Elastizitätsmodul verbunden, das auf der Registerkarte Allgemein eingegeben wurde. Daher kann die Dehnung für die erste Zeile nicht eingegeben werden. Sie wird vom Prozessor als (Spannung Zeile 1)/(Elastizitätsmodul) berechnet. Die Schnittstelle berechnet die Dehnung für die erste Zeile und gibt sie ein, wenn Sie versuchen, diese Zelle auszuwählen. Der Prozessor berechnet die anfängliche Dehnung unabhängig vom eingegebenen Wert.
Registerkarte Armierung
Die Eingaben auf der Registerkarte Armierung beziehen sich auf die Armierungsmaterialien. Eine bilineare Spannungs-Dehnungs-Kurve wird in der Analyse verwendet, wobei das Material dem Elastizitätsmodul bis zur Streckgrenze und dann dem Dehnungsverfestigungsmodul folgt.
- Anzahl Armierungen Wählen Sie die Anzahl der Armierungen aus, die in das Material eingeschlossen werden sollen. Verwenden Sie dafür die Dropdown-Menüs. Die entsprechenden Registerkarten Anzahl Armierungen stehen zur Eingabe von Daten zur Verfügung.
- Volumenverhältnis ist der Anteil des Gesamtvolumens, den die Armierung ausmacht. Dieser Wert muss zwischen 0 und 1 liegen, und die Summe der Volumenverhältnisse für alle Armierungen muss kleiner als 1 ist.
- Massendichte Geben Sie die Masse pro Volumeneinheit nur für das Armierungsmaterial ein.
- Elastizitätsmodul Geben Sie das Elastizitätsmodul des Armierungsmaterials im elastischen Bereich ein.
- Dehnungsverfestigungsmodul Das Dehnungsverfestigungsmodul ist die Steigung der Spannungs-Dehnungs-Kurve nach der Streckgrenze.
- Streckgrenze Geben Sie die Streckgrenze des Armierungsmaterials ein.
- Richtung X Armierung, Richtung Y Armierung und Richtung Z Armierung sind die X-, Y- und Z-Komponenten eines Vektors, der die Richtung der Armierung definiert. Somit gibt [1,0,0] an, dass die Armierungen parallel zur X-Achse liegen, und mit [1,1,0] werden die Armierungen auf der XY-Ebene in einem Winkel von 45 Grad von der X-Achse positioniert. Die Größe des Vektors muss größer als 0 sein, wird aber ansonsten nicht verwendet.
Registerkarte Erweitert
Die Bruchlinie für einfachen Beton kann entweder anhand der Stärken berechnet werden, die auf der Registerkarte Stärken eingegeben wurden, oder aus den tatsächlichen Testdaten. Verwenden Sie das Pulldown-Menü Methode, um anzugeben, welche Parameter in der Berechnung verwendet werden. Auf der Seite Armierter Beton - Theoretische Beschreibung finden Sie Informationen zum Berechnen des Koeffizienten basierend auf gemessenen Daten.