Gehäuseelemente

Gehäuseelemente sind isoparametrische vierseitige Elemente mit 4 bis 8 Knoten bzw. dreieckige Elemente mit 3 bis 6 Knoten in beliebiger 3D-Ausrichtung. Die Elemente mit 4 Knoten erfordern ein deutlich feineres Netz als die Elemente mit 8 Knoten, um konvergierenden Verschiebungen und Spannungen in Modellen mit Biegungen aus der Ebene heraus zu erzeugen. In Abbildung 1 sind einige typische Gehäuseelemente dargestellt.

Das allgemeine und gemeinsam rotierende Gehäuseelement wurden durch die Arbeit von Ahmad, Iron und Zienkiewicz formuliert und später durch Bathe und Balourchi präzisiert. Sie können für Probleme mit dicken und dünnen Gehäusen gleichermaßen auf Modelle angewendet werden. Darüber hinaus kann mit diesem Gehäuseelement die Geometrie eines doppelt gekrümmten Gehäuses mit variabler Dicke präzise beschrieben werden.

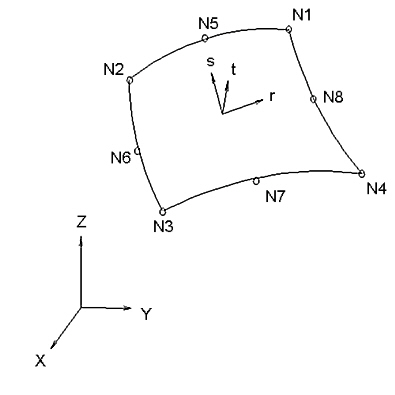
Abbildung 1: Beispiel für ein 3D-Gehäuseelement

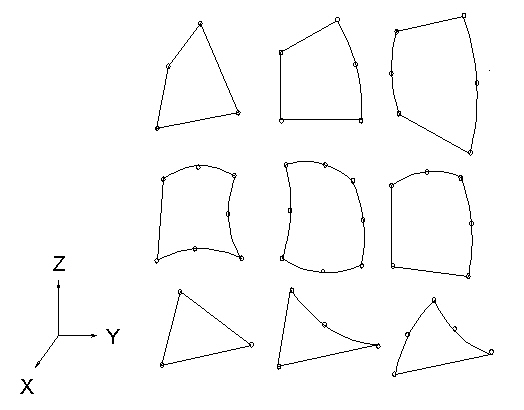
Abbildung 2: Typische Gehäuseelemente

Das dünne Gehäuseelement basiert auf der Theorie für dünne Platten. Das Biegeverhalten des Elements basiert auf dem Kirchoff-Ansatz für die Biegung von Platten unter Verwendung der Interpolationsfunktionen von Batoz. Die Formulierung erfüllt die Kirchoff-Abhängigkeiten entlang der Begrenzung und sorgt für eine lineare Variation der Krümmung durch das Element. Das Membranverhalten des Elements basiert auf dem Allman-Dreieck, das vom LST-Element (Linear Strain Triangular) abgeleitet wird. Eine Näherung für eine allgemeine gekrümmte Oberfläche wird bei diesem Element durch eine Reihe von Facetten erreicht, die aus den Ebenen bestehen, die durch die drei Knoten jedes Elemente gebildet werden. Aus diesen Gründen ist ein sorgfältig definiertes Netz erforderlich.

Die Elementgeometrie wird durch die Knotenpunktkoordinaten beschrieben. Jeder Gehäuseelementknoten verfügt über fünf Freiheitsgrade, drei Translations- und zwei Rotations-Freiheitsgrade. Die Translations-Freiheitsgrade befinden sich im globalen kartesischen Koordinatensystem. Die Rotationen erfolgen um zwei orthogonalen Achsen auf die Gehäuseoberfläche, die an jedem Knoten definiert sind. Auch die Beschränkungen und anliegenden Drehmomente in der Rotationsbegrenzungsbedingung verweisen auf dieses Knotenrotationssystem. Die beiden Drehachsen (V1 und V2) werden in der Regel automatisch durch den Gleichungslöser bestimmt und müssen nicht explizit ausgerichtet werden.

Die Drehungsrichtungen R1 und R2 an jedem Knoten werden durch das Kreuzprodukt des Normalenvektors Vn und eines Führungsvektors Vg wie folgt bestimmt. Siehe Abbildung 3 (V1 und V2 sind die Einheitsvektoren entlang der Drehrichtungen R1 und R2):

R1 = V2 x Vn

R2 = Vn x Vg

Der standardmäßige Führungsvektor Vg ist (1,0,0). Mit anderen Worten, die Achse R1 ist die Projektion des Führungsvektors Vg auf die Gehäuseoberfläche, und die Achse R2 liegt auf dieser Gehäuseoberfläche, jedoch orthogonal zu R1 und dem Normalenvektor Vn. Abbildung 3 zeigt die Ausrichtung von R1 und R2 bei Verwendung des standardmäßigen Führungsvektors (1,0,0).

Sie können zwei Führungsvektoren für jedes Gehäuseelementteil eingeben. Weist der Führungsvektor keine Projektion auf die Gehäuseebene auf, wird der zweite Führungsvektor verwendet. Sie können auch einen Führungsvektor für einen bestimmten Knoten angeben.

Die Gleichungslöser bestimmt die Normalenrichtung jedes Gehäuseelementknotens, indem der Durchschnitt aller Normalenvektoren aus verschiedenen Elementen mit einer Verbindung zum Knotenpunkt gebildet wird. Die Elementnormalen werden anhand der Daten für die Elementeckknoten berechnet. Ausgehend von diesem Normalenvektor werden dann zwei Rotationsachsen bestimmt. Sie können die Richtung des Normalenvektors auch direkt angeben und die Berechnungen des Gleichungslösers unterdrücken. Die beiden Rotationsvektoren können auch in einer benutzerdefinierten Richtung ausgerichtet werden, sodass auf einfache Weise verzerrte Rotationsbeschränkungen oder Drehmomente im 3D-Raum definiert werden können.

Wenn sich mehrere Gehäuseelemente in einem Bereich schneiden (in der Regel an einer Schnittlinie), lässt sich der Rotations-Freiheitsgrad an diesem Bereich nur schwer angeben. In diesem Fall sollten die Knoten in dem Bereich mit der Überschneidung als Freiheitsgrad mit 6 Knoten definiert werden.

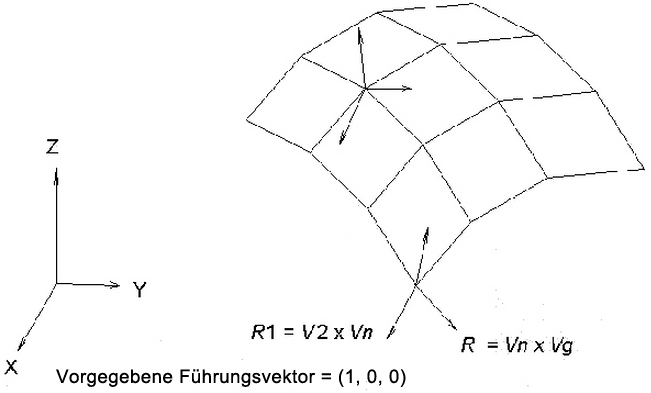
Abbildung 3: Mit Vg bestimmte Rotations-Freiheitsgrade

Bei sechs Freiheitsgradknoten werden global ausgerichtete Rotations-Freiheitsgrade verwendet anstelle der eindeutigen Freiheitsgrade R1 und R2 an jedem Knoten.

Dreidimensionale Gehäuseelemente sind Elemente vom Typ 26 isoparametrische vierseitige Elemente mit 4 bis 8 Knoten bzw. dreieckige Elemente mit 3 bis 6 Knoten in einer beliebigen 3D-Ausrichtung. Sie können für Probleme mit dicken und dünnen Gehäusen gleichermaßen auf Modelle angewendet werden. Darüber hinaus kann mit diesem Gehäuseelement die Geometrie eines doppelt gekrümmten Gehäuses mit variabler Dicke präzise beschrieben werden. Die theoretischen Aspekte dieser Elementformulierung finden Sie bei Bathe und Balourchi.

Die Elementgeometrie wird durch die Knotenpunktkoordinaten beschrieben. Jeder Gehäuseelementknoten verfügt über fünf Freiheitsgrade, drei Translations- und zwei Rotations-Freiheitsgrade. Die Rotations-Freiheitsgrad der Gehäuseelemente werden durch die Führungsvektoren des Gehäuses definiert. Die Projektion des Führungsvektors Vg auf das Gehäuseelement dient als erste Rotationsachse (R1). Die zweite Rotationsachse ist orthogonal zu R1 und zum Normalenvektor (Vn) des Gehäuses, wobei die Regel R2 = Vn x Vg gilt. Der standardmäßige Führungsvektor ist (1,0,0). Wenn der Führungsvektor parallel zum Normalenvektor Vn des Gehäuses ist, wird ein zweiter Führungsvektor [standardmäßig (0,1,0)] verwendet, um die Richtung R1 zu definieren.

Parameter für Gehäuseelemente

Es stehen drei Arten von Gehäuseelemente mit unterschiedlichen Optionen zur Verfügung. Der Unterschied zwischen den Typen wurde im vorherigen Abschnitt erläutert. Der Gehäuseelementtyp kann im Dropdown-Feld Elementerarbeitung auf der Registerkarte Erweitert des Bildschirms Elementdefinition ausgewählt werden. Die Standardauswahl basierend auf dem Materialmodell ist jedoch meist ausreichend.

Zuerst müssen Sie das Materialmodell für dieses Bauteil im Dropdown-Feld Materialmodell angeben. Folgende Gehäusematerialmodelle sind verfügbar:

Tipp: Eine höhere Integrationsreihenfolge (Einstellung auf der Registerkarte Erweitert) für hyperelastische Materialien trägt zur Konvergenz bei, wenn das Bauteil einer umfangreichen Verformung unterliegt.

Legen Sie die Dicke der Gehäuseelemente im Feld Dicke fest. Das Element wird auf der Mittelebene des Gehäuseelements gezeichnet. Sie müssen einen Wert für die Dicke eingeben, um die Analyse durchzuführen. Wenn die Option Komposite im Dropdown-Feld Materialmodell ausgewählt wurde, ist dieses Feld nicht verfügbar. In diesem Fall wird die Summe der Dicken von den auf der Registerkarte Komposite definierten Lagen in diesem Feld angezeigt.

Damit für die Gehäuseelemente in diesem Bauteil die Mittelknoten aktiviert werden, wählen Sie in der Dropdown-Liste Mittelknoten die Option Einbezogen aus. Wenn diese Option ausgewählt ist, sind für die Gehäuseelemente zusätzliche Knoten in der Mitte jeder Kante definiert. (Bei Netzen von CAD-Volumenkörpermodellen folgen mittlere Knoten der ursprünglichen Krümmung der CAD-Oberfläche, abhängig von der gewählten Option, bevor das Netz erstellt wurde. Bei handgefertigten Modellen und geänderten CAD-Modellnetzen befindet sich der mittlere Knoten in der Mitte zwischen Eckknoten.) Hierdurch wird ein Gehäuseelement mit 4 Knoten in ein Gehäuseelement mit 8 Knoten umgewandelt. Ein Element mit mittleren Knoten führt zu genaueren berechneten Abstufungen. Elemente mit mittleren Knoten verlängern die Verarbeitungszeit. Wenn das Netz ausreichend klein ist, wird mit den Mittelknoten u. U. kein wesentlich genaueres Ergebnis erzielt.

Verwenden Sie die Dropdown-Liste Analyseart, um den erwarteten Verschiebungstyp festzulegen. Kleine Verschiebung eignet sich für Bauteile, bei denen keine Bewegungen und nur kleine Dehnungen auftreten, und ignoriert alle geometrischen Effekte, die sich aus großen Verschiebungen ergeben. Große Verschiebungen eignet sich für Bauteile, die keine Bewegung und/oder große Dehnungen aufweisen. (Abhängig vom ausgewählten Gehäuseelementtyp können weitere Optionen für die Analyseformulierung auf der Registerkarte Erweitert verfügbar sein, auf die sich die Auswahl in der Dropdown-Liste Analysetyp auswirkt.)

Tipp:
  • Die Verschiebung an Mittelknoten wird immer ausgegeben. Bei der Spannung und Dehnung an den Mittelknoten handelt es sich nur um Ausgaben, wenn der Benutzer die Option zur Ausgabe dieser Ergebnisse vor der Durchführung der Analyse aktiviert. Die Option befindet sich im Dialogfeld SetupModell einrichten Parameter Erweitert auf der Registerkarte Ausgabe. (Weitere Informationen finden Sie unter Steuern der Ausgabedateien.)
  • Legen Sie auf der Registerkarte Optionen Analyse die Option Große Verschiebungen als Standard in nichtlinearen Analysen fest, um zu steuern, ob die Analyseart die Vorgabeeinstellungen für kleine oder große Verschiebungen übernimmt.

Verbundwerkstoffmodell

Wenn die Gehäuseelemente ein Verbundwerkstoffmodell verwenden, können Sie in der Dropdown-Liste Ausfallkriterium auf der Registerkarte Verbundwerkstoff des Dialogfelds Elementdefinition ein Ausfallkriterium auswählen. Die verfügbaren Optionen und die zugehörigen verwendeten Gleichungen sind:

[1]

Dabei gilt:

Xt = Axiale oder longitudinale Festigkeit bei Zug (>0)

Xc = Axiale oder longitudinale Festigkeit bei Druck (>0)

Yt = Transversale Festigkeit bei Zug (>0)

Yc = Transversale Festigkeit bei Druck (>0)

S = Scherfestigkeit

F12 = In die Materialeigenschaften eingegebener Spannungsinteraktionswert. Wenn Sie der Wert 0 beträgt, ist die Standardeinstellung .

σ1 = Spannung in Hauptmaterial , Richtung 1

σ2 = Spannung in Hauptmaterial, Richtung 2

τ12 = Scherspannung in Hauptmaterialebene 1-2

Wenn die Gleichung [1] nicht erfüllt ist, weist das Material einen Fehler auf.

[2]

wobei R das Festigkeit-Spannungs-Verhältnis angibt.

Da jede Kombination von Spannungskomponenten in [1] das Maximum erreicht, wenn die linke Seite Gleichheit erreicht, kann [2] in [1] ersetzt werden und folgendes Ergebnis liefern:

Wenn diese Gleichung nach R umgestellt wird, erhalten Sie Folgendes:

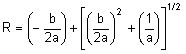
Dabei gilt:

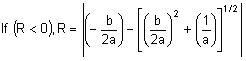
Die Vorzeichen der Spannungen σ ij werden umgekehrt.

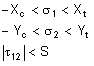
[3]

Dabei gilt:

σ1 = Berechnete Spannung in Richtung 1

σ2 = Berechnete Spannung in Richtung 2

τ12= berechnete Scherspannung

Xc = zulässige Druckspannung in Richtung 1 (> 0)

Yc = zulässige Druckspannung in Richtung 2 (> 0)

Xt = Zulässige Zugspannung in Richtung 1 (>0)

Yt = Zulässige Zugspannung in Richtung 2 (>0)

S = Zulässige Scherspannung (>0)

Wenn die drei Bedingungen der Gleichung [3] nicht erfüllt werden, weist das Material einen Fehler auf.

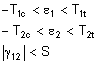
[4]

Dabei gilt:

ε1 = Berechnete Dehnung in Richtung 1

ε2 = Berechnete Dehnung in Richtung 2

γ = Berechnete Scherdehnung

T1c = Zulässige Druckdehnung in Richtung 1 (>0)

T2c = Zulässige Druckdehnung in Richtung 2 (>0)

T1t = Zulässige Zugdehnung in Richtung 1 (>0)

T2t = Zulässige Zugdehnung in Richtung 2 (>0)

S = Zulässige Scherdehnung (>0)

Wenn die Bedingungen der Gleichung [4] nicht erfüllt sind, weist das Material einen Fehler auf.

Die Tabelle Komposite-Laminatstapelsequenz kann verwendet werden, um die Verbundwerkstoff-Schichten zu definieren. Die Layer werden wie unten im Abschnitt Steuern der Ausrichtung von Gehäuseelementen beschrieben ausgerichtet und sortiert. Die Spalte Dicke muss für jeden Layer definiert werden. Die Spalte Ausrichtungswinkel gibt den Winkel α zwischen den Materialachsen (definiert auf der Registerkarte Ausrichtung) und den Faser- oder Layerachsen an. Die Materialeigenschaften werden entsprechend der Schichtachsen eingegeben. Klicken Sie zum Definieren der Materialeigenschaften für einen Layer in die Spalte Material. Ein Dialogfeld wird angezeigt, in dem Sie ein vorhandenes Material auswählen oder ein neues Material Hinzufügen können. (Weitere Informationen finden Sie unter Verbundwerkstoff-Materialeigenschaften.)

Tipp: Verwenden Sie die Schaltfläche Zeile kopieren, um vorhandene Eingaben zu kopieren und Wiederholungsserien zu erstellen. Geben Sie entweder eine einzelne zu kopierende Schicht oder einen Bereich von Schichten, getrennt durch einen Bindestrich (-) an, z. B. 4-8. Geben Sie im Feld Vor Zeile einfügen eine beliebige Zeilennummer nach dem letzten Eintrag an, um eine Kopie am Ende der Stapelsequenz einzufügen.

Definieren der thermischen Eigenschaften von Gehäuseelementen

Wenn ein Gehäuseelementteil ein thermoelestisches oder temperaturabhängiges Materialmodell verwendet, müssen Sie im Feld Spannungsfreie Referenztemperatur auf der Registerkarte Thermisch des Dialogfelds Elementdefinition einen Wert festlegen. Dieser Wert wird als Referenztemperatur verwendet, um elementbasierte Lasten zu berechnen, die mittels bilinearer Interpolation von Knotentemperaturen einer Abhängigkeit mit thermischem Wachstum zugewiesen wurde.

Steuern der Ausrichtung von Gehäuseelementen

Es gibt zwei Arten von Achsen, die der Benutzer steuern kann. Einer der Typen ist die senkrecht den Gehäuseelementen stehende Achse. Der Hauptgrund für die senkrechte Richtung ist zum Anwenden von Druck auf das Element oder die Angabe von Fläche-zu-Fläche-Kontakt. Bei Verbundwerkstoffen steuert die Normalenrichtung, auf welcher Seite des Elements sich Layer 1 befindet. Der zweite Typ Achsen sind die Achsen in der Ebene des Elements. Diese sind bei der Arbeit mit einem orthotropen Materialmodell oder zum Anzeigen der Ergebnisse im Elementkoordinatensystem hilfreich.

Zusätzlich zu diesen beiden Typen gibt es drei Achsensysteme, die der Benutzer möglicherweise festlegen muss:

Elementachsen:

Eine Element-Knotennormale wird verwendet, um die Ausrichtung der Normalenachse des Elements (+ 3) zu steuern, oder welche Seite des Elements die Oberseite (+ 3) und die Unterseite (-3) ist. Die Normalenrichtung wird durch Festlegen eines Punkts im Raum über die Felder X-Koordinate, Y-Koordinate und Z-Koordinate im Abschnitt Element-Normale der Registerkarte Ausrichtung bestimmt. Siehe Abbildung 4. Ein positiver Normaldruck wird normal auf die Gehäuseelemente in Richtung der Achse +3 angewendet und zeigt daher weg von der Element-Knotennormale.

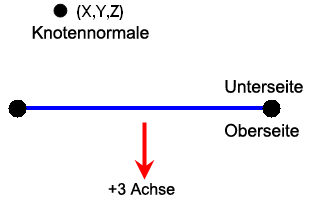
Abbildung 3: Festlegen der Element-Normalen

Die Kantenansicht des Gehäuseelements wird dargestellt. 

Für eine allgemeine FEM-Analyse können Sie die Ausrichtung des Elements in der Ebene ignorieren (Achse 1 und 2). Die Möglichkeit zum Ausrichten der ebenen Achsen von Elementen ist bei Elementen mit orthotropen Materialmodellen und zusammengesetzten Elementen hilfreich. Die Ausrichtung der Achsen 1 und 2 erfolgt auf der Registerkarte Ausrichtung des Dialogfelds Elementdefinition.

Die Dropdown-Liste Methode enthält drei Optionen, mit denen Sie festlegen können, welche Seite des Elements die IJ-Seite sein soll. Die Elementachse 1 ist parallel zur IJ-Seite des Elements. (Elementachse 2 bildet ein Rechte-Hand-System mit den Achsen 1 und 3.)

Materialachse:

Die Materialeigenschaften werden in Form von Materialachsen für orthotrope Materialien eingegeben. Die Definition der Materialachsen erfolgt aus den Elementachsen (oder aus einer globalen Referenz) im Abschnitt Materialachsenrichtung auf der Registerkarte Ausrichtung des Dialogfelds Elementdefinition. (Materialeigenschaften für zusammengesetzte Materialien werden in Form von Schichtachsen eingegeben, wie unten beschrieben.)

In allen Fällen liegt die Materialachse 3 senkrecht zum Element und in der gleichen Richtung wie die Elementachse 3.

Wenn die erweiterten Gehäuseelemente ein orthotropes Materialmodell oder ein Verbundwerkstoffmodell verwenden, können die Materialachsen 1 und 2 in der Ebene wie folgt definiert werden:

Unabhängig von der Methode, die zum Ausrichten der Materialachsen des gemeinsam rotierenden Gehäuseelements verwendet wurde, können Sie mit dem Feld Drehwinkel auf gleichem Layer die Materialachsen um einen bestimmten Winkel um die Achse 3 drehen. Die Drehung befolgt die Rechte-Hand-Regel um Achse 3.

Wenn die allgemeinen Gehäuseelemente ein orthotropes Materialmodell verwenden, können die Materialachsen in der Ebene 1 und 2 mittels zwei Methoden ausgerichtet werden. Bei der ersten Methode wird ein Vektor parallel zu Materialachse 1 in den Feldern X-Richtung, Y-Richtung, und Z-Richtung angegeben. Materialachse 2 befindet sich in der Ebene des Elements und bildet ein Rechte-Hand-System mit den Achsen 1 und 3. Bei der zweiten Methoden definieren Sie einen Winkel im Feld Materialachsen-Drehungswinkel, durch den Materialachse 1 mithilfe der Rechte-Hand-Regel um Elementachse 3 gedreht wird (siehe Abbildung 5). Diese Methode wird nur verwendet, wenn die Werte in den Feldern X-Richtung, Y-Richtung und Z-Richtung 0 sind.

 

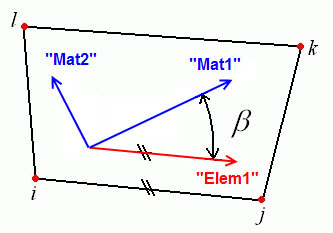
Abbildung 5: Definition des Rotationswinkels der Materialachsenrichtung

Schichtachsen:

Bei Verbundwerkstoffen verfügt jeder Layer der Schicht über einen Satz lokaler Achsen. Die Layerachse 1 ist die Achse entlang der Faser jedes einzelnen Layers. Die Layerachse 2 ist lotrecht zur Faser jedes einzelnen Layers in der Elementebene angeordnet. Die Achse von Schicht 3 ist senkrecht zum Element und deshalb parallel zur lokalen Elementachse C. (Um Verwechslungen zwischen den Schichtachsen und den Elementachsen auszuschließen, werden die Elementachsen beim Arbeiten mit zusammengesetzten Elementen häufig als A-B-C bezeichnet, und die Achsen 1-2-3 definieren die Ausrichtung der Fasern.) Siehe Abbildungen 6 und 7.

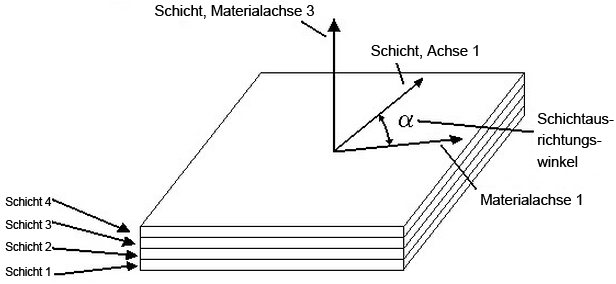
Abbildung 6: Laminatstapelsequenz

Der Benutzer gibt den Winkel a für jeden Layer im Feld Ausrichtungswinkel der Tabelle Komposite-Laminatstapelsequenz ein. Achse 3 wird durch die Koordinaten der Elementnormalen gesteuert.

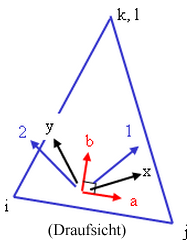
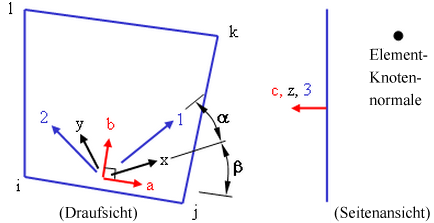
Abbildung 7: Alternative Darstellung von Element-, Material- und Layerachsen

Die Elementachsen a-b-c werden außerhalb der Koordinaten der Elementnormalen und der Seite ij des Elements angeordnet. Die Materialachsen x-y-z werden um den Winkel b zu den Elementachsen gedreht. Die Element- und Materialachsen sind für alle Layer im Stapel gleich. Die Layer- oder Faserachsen 1-2-3 werden um den Winkel β um die Materialachsen gedreht. Der Winkel kann für jede Schicht im Stapel unterschiedlich sein.

Erweiterte Parameter für Gehäuseelemente

Wählen Sie in der Dropdown-Liste Analysebeschreibung auf der Registerkarte Erweitert die Formulierungsmethode aus, die Sie für die Gehäuseelemente verwenden möchten.

Wenn das Kontrollkästchen Überlappen der Elemente zulassen aktiviert ist, wird beim Dekodieren der Linien in Elemente die Erstellung überlappender Elemente zugelassen. Eine Überlappung kann bei der Modellierung von Elementen erforderlich sein. Dies gilt besonders für Probleme, die auf planare Bewegung beschränkt sind.

Damit die Spannungsergebnisse für jedes Element bei jedem Zeitschritt während der Analyse in die Protokolldatei geschrieben werden, aktivieren Sie das Kontrollkästchen Detaillierte Spannungsausgabe. Dies kann zu großen Ausgabemengen führen.

Wenn eines der von Mises-Materialmodelle ausgewählt wurde, können Sie wählen, ob der aktuelle Materialstatus (elastisch oder plastisch), die aktuelle Streckgrenze, die aktuelle Fließspannungsgrenze, die zugehörige Spannungsgrenze und die entsprechende Ausgabe für plastische Spannung an Eckknoten und/oder Integrationspunkten bei jedem Zeitschritt vorhanden sein sollen. Wählen Sie dazu die entsprechende Option in der Dropdown-Liste Weitere Ausgabe aus.

Wenn Sie allgemeine Gehäuseelemente verwenden, wählen Sie in der Dropdown-Liste Integrationsreihenfolge die für dieses Bauteil verwendete Integrationsreihenfolge aus. Wählen Sie für rechteckig geformte Elemente die Optionzweitrangig. Für leicht verformte Elemente wählen Sie die Option3. Ordnung. Für extrem verformte Elemente wählen Sie die Option 4. Ordnung. Die Berechnungszeit für die Formulierung der Elementsteifigkeit erhöht sich mit der dritten Potenz der Integrationsreihenfolge. Aus diesem Grund sollte die geringste Integrationsreihenfolge, die zu akzeptablen Ergebnissen führt, verwendet werden, sodass die Verarbeitungszeit verkürzt wird.

Mithilfe des reduzierten Integrationsschemas kann das Schersperrverhalten für gekrümmte Gehäusekonfigurationen verbessert werden, indem Sie das Kontrollkästchen Reduzierte Integration für Membranscherausdrücke oder Reduzierte Integration für Querscherausdrücke aktivieren. Wenn die Dicke der Gehäuseelemente weniger als 1/10 der Länge oder Höhe beträgt, wird die reduzierte Integration empfohlen. Wenn die Dicke der Gehäuseelemente mehr als 1/10 der Länge oder Höhe beträgt, wird die vollständige Integration empfohlen.

So ermitteln Sie, ob Schalenelemente dick oder dünn sind:

Die Schlankheit der Schalenelemente wird an der charakteristischen Länge der einzelnen Elemente gemessen. Die Schlankheit ist definiert als Stärke, dividiert durch die charakteristische Länge. So ermitteln Sie die charakteristische Länge und Dicke:

  • Verwenden Sie die Option Extras Messen, und klicken Sie anschließend auf zwei Scheitelpunkte, um die Entfernung zwischen diesen Punkten zu erhalten.
  • Die Dicke der Schalenelemente wird auf der Registerkarte Allgemein des Dialogfelds Elementdefinition definiert.
  • Verwenden Sie alternativ die Option Extras Min./Max. Länge, um die minimale und die maximale Länge der Linien zu bestimmen, aus denen sich das Modell zusammensetzt. Dies ist ein globales Werkzeug; blenden Sie daher die Bauteile aus, die beim Ermitteln der Länge nicht einbezogen werden sollen.

Anmerkung: Die Schalenelementformulierung Allgemein kann sowohl für dicke als auch dünne Schalen verwendet werden. Darüber hinaus können Sie das Modell mit der entsprechenden Analyseformulierung oder der Option Reduzierte Integration für Querscherausdrücke genauer definieren. Diese Einstellungen befinden sich auf der Registerkarte Weitere im Dialogfeld Elementdefinition. Berücksichtigen Sie bei der Auswahl der Elementformulierungen und Optionen die folgenden Punkte:

  • Schlankheit > 1/10:

    Dicke Schalen sind erforderlich, wenn die Querschubsteifigkeit wichtig ist (d. h., wenn die Berücksichtigung des Querschubs erhebliche Auswirkungen auf die Ergebnisse hat). Für homogene, isotrope Schalenelemente ist die Querschubsteifigkeit dann wichtig, wenn die Schlankheit mehr als 1/10 beträgt. Verwenden Sie aus diesem Grund Schalen des Typs Allgemein, und aktivieren Sie in diesen Fällen nicht die Option Reduzierte Integration für Querscherausdrücke.

  • Schlankheit <= 1/10:

    Dünne Schalen werden benötigt, wenn die Querschersteifigkeit gering oder unbedeutend ist und wenn die Kirchhoff-Abhängigkeit (siehe weiter unten) ordnungsgemäß erfüllt werden muss. Bei homogenen Schalen ist dies der Fall, wenn die Schlankheit weniger als 1/10 beträgt. Sie können daher in diesen Fällen Schalen des Typs Dünn angeben oder aber Schalen des Typs Allgemein verwenden und die Option Reduzierte Integration für Querscherausdrücke aktivieren.

  • Die Option Reduzierte Integration für Querscherausdrücke gilt für alle nichtlinearen Analysen, bei denen Schalenelemente des Typs Allgemein verwendet werden [MES, Statische Spannung mit nichtlinearen Materialmodellen, Eigenfrequenz (Modal) mit nichtlinearen Materialmodellen, MES-Riks-Analysen].
Wichtig:
  • Bei Schalen des Typs Allgemein kann eine Schersperrung auftreten. Wenn Sie allgemeine Schalen für dünne Elemente verwenden und eine Schersperrung auftritt, können Sie gegebenenfalls die Option Reduzierte Integration für Querscherausdrücke aktivieren. Die Schersperrung zeichnet sich durch eine stark unterschätzte Schubverschiebung aus. Bei nichtlinearen Modalanalysen kann dieses Phänomen dazu führen, dass übermäßig hohe Eigenfrequenzen berechnet werden.
  • Bei diesem Schersperrphänomen wird in der Regel eine reduzierte Konvergenzrate für grobe Netze verwendet, unabhängig von kritischen Parametern (z. B. hochfrequenten Schwingungen oder anderen Arten von Instabilität in der Struktur). Es empfiehlt sich, zunächst die Netzqualität oder Probleme mit übermäßiger Grobheit zu überprüfen, bevor Sie die Verwendung der Option Reduzierte Integration für Querscherausdrücke in Betracht ziehen, falls die Schlankheit weiterhin einen Wert von kleiner oder gleich 1/10 aufweist.

Kirchhoff-Abhängigkeit:

In der Theorie dünner Schalen bleibt die Elementnormale orthogonal zur Schalenreferenzfläche (dies wird als "Kirchhoff-Abhängigkeit" bezeichnet). Dies ist in der folgenden Abbildung grafisch dargestellt. Die rote Linie stellt die Elementnormale dar, und die magentafarbenen Linien sind die Kanten der Mittelebene (Referenzfläche):

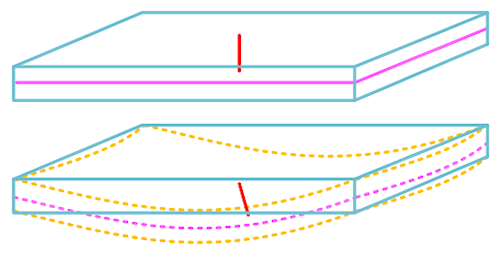
Gemeinsam rotierende Schalenelemente

Zusätzlich zu den Gehäuseelementen des Typs Allgemein und Dünn steht auch die Schalenelementformulierung Gemeinsam rotierend zur Verfügung. Diese Formulierung stellt stabile Lösungen für Verbund- und Thermo-Materialmodelle bereit. Das Schalenelement Gemeinsam rotierend wurde zuvor als "Erweitert" bezeichnet.

Für gemeinsam rotierende Gehäuseelemente kann das Kontrollkästchen Bohrenden DOF unterdrücken aktiviert werden, um das Konvergieren der Modelle zu unterstützen. Diese Option kann nur verwendet werden, wenn kein lokales Koordinatensystem im Modell verwendet wird.

Grundlegende Schritte für die Verwendung von Gehäuseelementen

  1. Stellen Sie sicher, dass ein Einheitensystem definiert ist.
  2. Stellen Sie sicher, dass das Modell einen nichtlinearen Analysetyp verwendet.
  3. Klicken Sie mit der rechten Maustaste auf die Überschrift Elementtyp für das Bauteil, das als Gehäuseelement definiert werden soll.
  4. Wählen Sie den Befehl Gehäuse aus.
  5. Klicken Sie mit der rechten Maustaste auf die Überschrift Elementdefinition.
  6. Wählen Sie den Befehl Elementdefinition bearbeiten.
  7. Wählen Sie auf der Registerkarte Allgemein das gewünschte Materialmodell im Dropdown-Feld Materialmodell aus.
  8. Geben Sie die Dicke der Gehäuseelemente ein. Diese Informationen sind erforderlich, und ohne diese Eingabe wird das Modell nicht ausgeführt.
  9. Wenn die Option Komposite oder Temperaturabhängige Komposite in der Dropdown-Liste Materialmodell ausgewählt ist, geben Sie die entsprechenden Daten auf der Registerkarte Komposite an.
  10. Klicken Sie auf die Registerkarte Ausrichtung.
  11. Geben Sie eine Element-Knotennormale an. Die Oberseite des Gehäuseelements zeigt immer weg von diesem Punkt.
  12. Klicken Sie auf OK.

Übergeordnetes Thema: Planare Elemente