Zentrifugallast

Anmerkung: Die Informationen in diesem Abschnitt gelten für alle linearen und nichtlinearen Analysen, die Zentrifugallasten unterstützen.

Eine Zentrifugallast simuliert die Effekte des gesamten Modells, wenn es um eine von Ihnen festgelegte Achse gedreht wird. Es sind nur Bauteile mit einer Materialmassendichte ungleich Null betroffen. Das Modell wird nicht wirklich gedreht. Es werden vielmehr die entsprechenden Kräfte, die aufgrund der Winkeldrehung und/oder Winkelbeschleunigung entstehen, berechnet und auf die Knoten der einzelnen Elemente angewendet.

Lineare Analysen

Es gibt drei Arten von linearen Analysen, die Zentrifugallasten unterstützen: Statische Spannung mit linearen Materialmodellen, Eigenfrequenz (Modal) mit Lastversteifung und kritische Knicklast. Das Modell kann sich mit einer konstanten Geschwindigkeit drehen und/oder eine konstante Winkelbeschleunigung erfahren.

Der Implementierungsbefehl unterscheidet sich bei den linearen Analysen geringfügig. In allen drei Fällen wird die tatsächliche Last auf der Registerkarte Zentrifugal des Dialogfelds Analyseparameter festgelegt. Die Drehachse und die Achse der Winkelbeschleunigung können durch jeden beliebigen Punkt im dreidimensionalen Raum verlaufen (d. h. die Achsen müssen nicht durch den Ursprung des globalen Koordinatensystem laufen). Die Unterschiede sind folgende:

• Statische Spannung mit linearen Materialmodellen:
  • Es gibt drei Möglichkeiten, um auf die Zentrifugallast zuzugreifen:
    1. Klicken Sie mit der rechten Maustaste im Browser (Strukturansicht) auf die Überschrift Zentrifugal unter der Überschrift Analyseart, und wählen Sie den Befehl Bearbeiten.
    2. Wählen Sie in der Multifunktionsleiste den Befehl Setup Lasten Zentrifugal.
    3. Öffnen Sie das Dialogfeld Analyseparameter (über den Browser oder die Multifunktionsleiste), und klicken Sie auf die Registerkarte Zentrifugal.
  • Globale Lastfall-Multiplikatoren steuern separat, ob die Lasten der Winkelgeschwindigkeit (Omega) und/oder der Winkelbeschleunigung (Alpha), die auf der Registerkarte Zentrifugal festgelegt wurden, für alle Lastfälle aktiv sind.
  • Die Achse der Winkelgeschwindigkeit und die Achse der Winkelbeschleunigung können einzeln definiert werden und können identisch oder unterschiedlich sein.
  • Die Achsen der Winkelgeschwindigkeit und der Winkelbeschleunigung können entlang einer beliebigen Linie im dreidimensionalen Raum verlaufen, so wie durch die Richtungsvektoren festgelegt.
• Eigenfrequenz (Modal) mit Lastversteifung und kritische Knicklast:
  • Auf die Zentrifugallast kann auf zwei Arten zugegriffen werden:
    1. Wählen Sie in der Multifunktionsleiste den Befehl Setup Lasten Zentrifugal.
    2. Öffnen Sie das Dialogfeld Analyseparameter (über den Browser oder die Multifunktionsleiste), und klicken Sie auf die Registerkarte Zentrifugal.
  • Für die Zentrifugallast gibt es keine globalen Lastfall-Multiplikatoren. Sie wird nur über das Kontrollkästchen Festgelegte Zentrifugallast einbeziehen auf der Registerkarte Zentrifugal des Dialogfelds Analyseparameter aktiviert. Wenn diese Option aktiviert ist, wirkt sich die Zentrifugallast auf alle resultierenden Modusformen, Modalfrequenzen und Knickfaktoren aus.
  • Die Drehachse und die Achse der Winkelbeschleunigung muss identisch sein (nicht einzeln festgelegt).
  • Die Drehachse und die Achse der Winkelbeschleunigung muss eine der drei globalen Achsen (x, y oder z) sein.

Nichtlineare Analysen

Zwei Arten von nichtlinearen Analysen unterstützen Zentrifugallasten:MES und statische Spannung mit nichtlinearen Materialmodellen. Lastkurven steuern sowohl die Drehgeschwindigkeit als auch die Winkelbeschleunigung im Verlauf der Zeit. Für beide Geschwindigkeiten kann dieselbe Lastkurve verwendet werden. Sie können jedoch auch zwei unterschiedliche Lastkurven für Dreh- und Winkelgeschwindigkeit festlegen. Die Zentrifugallast wird auf der Registerkarte Zentrifugal des Dialogfelds Weitere Einstellungen Analyseparameter definiert. Sie können mittels folgender zwei Methoden darauf zugreifen:

1. Wählen Sie in der Multifunktionsleiste den Befehl Setup Lasten Zentrifugal.
2. Öffnen Sie das Dialogfeld Analyseparameter (über den Browser oder die Multifunktionsleiste), und klicken Sie auf die Schaltfläche Erweitert und dann auf die Registerkarte Zentrifugal.

Für beide Arten der nichtlinearen Analyse, die Zentrifugallasten unterstützen, gilt:

• Die Drehachse und die Achse der Winkelbeschleunigung können einzeln definiert werden und können identisch oder unterschiedlich sein.
• Die Drehachse und die Achse Winkelbeschleunigung können durch einen beliebigen Punkt im dreidimensionalen Raum verlaufen (d. h. die Achsen müssen nicht durch den Ursprung des globalen Koordinatensystems laufen).
• Die Drehachse und die Achse der Winkelbeschleunigung können entlang einer beliebigen Linie im dreidimensionalen Raum verlaufen, so wie durch die Richtungsvektoren festgelegt.

Anwenden von Zentrifugallasten

So wenden Sie eine Zentrifugallast auf ein Modell an

1. Öffnen Sie das entsprechende Dialogfeld mittels einer der oben beschriebenen Methoden (kann je nach Analyseart unterschiedlich sein).
2. Aktivieren Sie (sofern im Dialogfeld vorhanden) das Kontrollkästchen Festgelegte Zentrifugallast einbeziehen.
3. Geben Sie die entsprechenden Größen unter Winkelgeschwindigkeit (Omega) und Winkelbeschleunigung (Alpha) an.
4. Wählen Sie bei nichtlinearen Analysen die Lastkurvennummern für die Winkelgeschwindigkeit und die Winkelbeschleunigung aus.
5. Geben Sie die Ausrichtung der Achse mit einer der oben beschriebenen Methoden an (kann je nach Analyseart unterschiedlich sein). Für einige Analysearten können die Drehachse und die Achse der Winkelbeschleunigung unterschiedlich sein, bei anderen Analysearten muss u. U. dieselbe Achse für beide verwendet werden (siehe oben). Außerdem unterstützen einige Analysearten nicht globale Achsenausrichtungen, es gibt auch Analysearten, die diese nicht unterstützen (siehe oben). Geben Sie mithilfe der Koordinaten Punkt auf Achse und Richtung oder mithilfe des Pulldown-Menüs für globale Achsen die Position und Richtung der Achse (oder Achsen) an. Die Winkeldrehung folgt der Rechte-Hand-Regel für den Vektor, den Sie definieren.
6. Legen Sie bei linear-statischen Spannungsanalysen die globalen Lastfall-Multiplikatoren Omega und/oder Alpha auf der Registerkarte Multiplikatoren des Dialogfelds Analyseparameter fest.
   Tipp: Bei einem Multiplikator ungleich Null muss die Last aktiviert werden. Weitere Informationen finden Sie unter Analyseparameter: Statische Spannung mit linearen Materialmodellen.

Verwenden Sie beispielsweise den Kreis, der am Ursprung in Abbildung 1 zentriert ist. Um die Drehung um die z-Achse am Ursprung festzulegen, geben Sie für Punkt auf Achse die Koordinaten (0,0,0) und für Richtung die Koordinaten (0,0,1) ein. Der Kreis dreht sich um seinen Mittelpunkt, der Mittelpunkt des Kreises bleibt stationär.

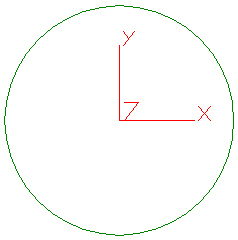
Abbildung 1: Modell 1, das sich um den Ursprung dreht

Wenn der Kreis wie in Abbildung 2 dargestellt bei (3,0,0) mit den gleichen Einstellungen für die Zentrifugallast zentriert ist, basiert die Last auf der Drehung des Kreises um den Ursprung. Mit anderen Worten, der Mittelpunkt des Kreises bewegt sich in einem kreisförmigen Pfad um den globalen Ursprung. Abbildung 3 zeigt eine grafische Darstellung des Pfads für den Kreis aus Abbildung 2 unter der angegebenen Zentrifugallast.

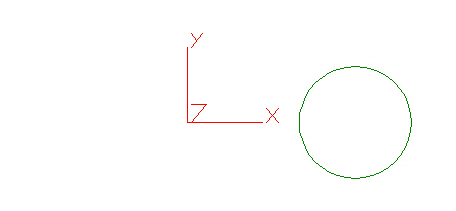
Abbildung 2: Modell 2 - Kreis, dessen Mittelpunkt nicht am globalen Ursprung liegt

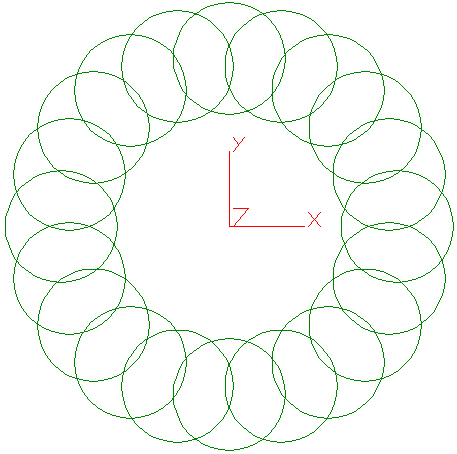
Abbildung 3: Interpretation von Modell 2, das sich um den Ursprung dreht

Anmerkung: Denken Sie bei allen drei linearen Analysen, die Zentrifugallasten unterstützen, daran, dass es sich trotz der simuliertem Bewegungseffekte um statische Analysen handelt. Daher muss das Modell in allen Richtungen statisch stabil sein. In der Regel ist ein rotierendes Bauteil oder eine Baugruppe mit einer Welle oder einem Hebel verbunden. Zwei gängige Abhängigkeitsschemata sind nachfolgend beschrieben:

• Verankern Sie die Montagefläche oder -flächen vollständig an der Trägerwelle oder am Hebel.
• Alternativ können Sie die tangentiale Bewegung entlang der Fläche der Bohrung mit Abhängigkeiten versehen, dort, wo die rotierenden Bauteile an der Welle oder dem Hebel fixiert werden. Durch diese Abhängigkeit werden automatisch zwei der drei Translationsfreiheitsgrade erzeugt. Bestimmen Sie zusätzlich noch einen Punkt, eine Kante oder eine Fläche gegen die Verschiebung in axialer Richtung. Machen Sie z. B. den Kontaktbereich der Wellenschulter gegen die Verschiebung in senkrechte Richtung abhängig, wodurch die axiale Bewegung unter Schublasten verhindert wird und der dritte Translationsfreiheitsgrad erzeugt wird.