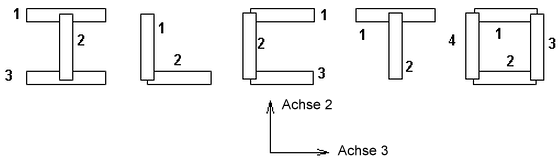
Nichtlineare Balkenelemente können Ergebnisse in drei verschiedenen ASCII-Textdateien ausgeben, je nachdem, welche Optionen unter der Elementdefinition ausgewählt wurden. (Weitere Informationen finden Sie im vorherigen Abschnitt Balkenelemente: Erweiterte Parameter für Balkenelemente).
Kräfte und Momente
Wenn Detaillierte Ausgabe von Kräften und Momenten aktiviert ist, werden die Kräfte und Momente im Balkenelement-Bauteil in die Übersichtsdatei (.al) geschrieben. Diese Datei hat folgendes Format:
Elem Node Force-1 Force-2 Force-3 Torque-1 Moment-2 Moment-3
Dabei gilt:
- Elem ist die Elementnummer. Jedes Bauteil beginnt bei Elementnummer 1.
- Node ist der lokale Elementknoten. Node 1 ist der I-Knoten und Node 2 ist die J-Knoten.
- Force-1 ist die Axialkraft in der Richtung der Achse 1.
- Force-2 ist die Schubkraft in der Richtung der Achse 2.
- Force-3 ist die Schubkraft in der Richtung der Achse 3.
- Torque-1 ist das Drehmoment um Achse 1.
- Moment-2 ist das Moment um Achse 2.
- Moment-3 ist das Moment um Achse 3.
Wenn das Material kein nichtlineares Verhalten (z. B. Plastizität) aufweist und der Benutzer die Position der neutralen Achse kennt, kann die Spannung einfach anhand der vorgegebenen Geometrie-, Kraft- und Momentdaten berechnet werden. Wenn das Material jedoch Streck- oder nichtlineares Verhalten aufweist, kann die Spannung nicht einfach aus diesen Daten berechnet werden. In solchen Fällen verwenden Sie die Spannungsausgabe (oder Dehnungsausgabe).
Spannung und Dehnung
Wenn Detaillierte Spannungsausgabe oder Detaillierte Dehnungsausgabe aktiviert ist, werden die Spannungen und Dehnungen im Balkenelement-Bauteil in die Ausgabedateien für Balkenspannung (.bso) und Balkendehnung (.bst) geschrieben. Das Format dieser Textdateien ist identisch und sieht folgendermaßen aus:
Element Axial-Int Sec# Int2 Int3 State Stress-11 Stress-12 Stress-13
oder
Element Axial-Int Sec# Int2 Int3 State Strain-11 Strain-12 Strain-13
Dabei gilt:
- Element ist die Elementnummer.
- Axial-Int ist der Integrationspunkt in Axialrichtung (1 Achse) und wird beginnend bei 1 in der vom Benutzer festgelegten Integrationsreihenfolge (maximal 7) erhöht.
- Sec# ist die Schnittnummer (wenn Querschnitt wie eine Reihe von Rechtecken behandelt wird).
- Int2 ist der Integrationspunkt in lokaler Y-Richtung (2 Achse) und wird beginnend bei 1 in der vom Benutzer festgelegten Integrationsreihenfolge (maximal 7) erhöht.
- Int3 ist der Integrationspunkt in lokaler Z-Richtung (3 Achse) und wird beginnend bei 1 in der vom Benutzer festgelegten Integrationsreihenfolge (maximal 7) erhöht.
- State zeigt an, ob der Punkt elastisch oder plastisch ist.
- Stress-11 ist die normale Spannung in der 11 Richtung.
- Stress-12 ist die Schubspannung in der 12 Richtung.
- Stress-13 ist die Schubspannung in der 13 Richtung.
- Strain-11 ist die normale Dehnung in der 11 Richtung.
- Strain-12 ist die Scherdehnung in der 12 Richtung.
- Strain-13 ist die Scherdehnung in der 13 Richtung.
Stellen Sie sich vor, dass das Balkenelement aus zahlreichen Integrationspunkten in alle drei Richtungen (Achse 1 entlang der Länge, Achse 2 und 3 in der Ebene des Querschnitts) besteht. Die Spannungsausgabe erfolgt an alle Integrationspunkten, für den Integrationsgrad wird daher 2x2x2 festgelegt. Jedes Element gibt dann 8 Spannungslinien für jedes Element aus.
Suchen Sie die 3D-Position (X, Y, Z) des Integrationspunkts (Int1, Int2, Int3) innerhalb des Elements. Dazu werden abhängig von der Form die folgenden Berechnungen verwendet.
Rechteck
Y = C(Int2,INTy)*Höhe*0,5, gemessen von der neutralen Achse in der Richtung der Achse 2
Z = C(Int3,INTz)*Breite*0,5, gemessen von der neutralen Achse in der Richtung der Achse 3
Kreis
R = Radius/2
R = R + C(Int2,INTy)*R
α = (2π/INTz)*(Int3-1)
Y = R*cosα, gemessen von der neutralen Achse in die Richtung der Achse 2
Z = R*sinα, gemessen von der neutralen Achse in die Richtung der Achse 3
Hohlkreis
R = (Ro+Ri)/2
R = R + C(Int2,INTy)*(Ro-Ri)/2
α = (2π/INTz)*(Int3-1)
Y = R*cos(α), gemessen von der neutralen Achse in die Richtung der Achse 2
Z = R*sin(α), gemessen von der neutralen Achse in die Richtung der Achse 3
Dabei gilt:
- X = C(Axial-Int,INTx)*0,5*Länge+0,5*Länge, gemessen vom I-Knoten (= Knoten 1)
- INTx ist die Gesamtanzahl der Integrationspunkte in x-dir (Integrationsgrad in lokal-1-Achse)
- INTy ist die Gesamtanzahl der Integrationspunkte in y-dir (Integration in lokal-2-Achse)
- INTz ist die Gesamtanzahl der Integrationspunkte in z-dir (Integration in lokal-3-Achse)
und die Menge C (i, Integrationsgrad) anhand der folgenden Tabelle:
| Integrationsgrad | C (i, Integrationsgrad) | ||||||
|---|---|---|---|---|---|---|---|
| i | i = 2 | i = 3 | i = 4 | i = 5 | i | i | |
| 1 | 0 | - | - | - | - | - | - |
| 2 | -1 | 1 | - | - | - | - | - |
| 3 | -1 | 0 | 1 | - | - | - | - |
| 4 | -1 | -0,333 | 0,333 | 1 | - | - | - |
| 5 | -1 | -0,5 | 0 | 0,5 | 1 | - | - |
| 6 | -1 | -0,6 | -0,2 | 0,2 | 0,6 | 1 | - |
| 7 | -1 | -0,666 | -0,333 | 0 | 0,333 | 0,666 | 1 |
Allgemeiner Querschnitt
Jeder Querschnitt wird separat wie ein unabhängiges Viereck behandelt. C (i, j) kann direkt angewendet werden, um die Position zu finden.
Vordefinierter Querschnitt
Jeder Querschnitt wird separat wie ein unabhängiges Viereck behandelt (siehe unten), wobei die Querschnittnummer angezeigt wird.