Verbundwerkstoff-Materialeigenschaften

Verbundwerkstoff-Materialeigenschaften werden nur für dünne und dicke Verbundelemente verwendet. Um die Eigenschaften richtig einzugeben, müssen die Materialachsen im Dialogfeld Elementdefinition definiert werden. (Weitere Informationen finden Sie auf den Seiten Dicke Verbundwerkstoffelemente und Dünne Verbundwerkstoffelemente.)

Die Verbundwerkstoff-Materialeigenschaften sind unten aufgeführt. Je nach Elementtyp, Analysetyp und Lasten sind möglicherweise nicht alle Eigenschaften des Materials erforderlich. Zusätzlich zu diesen Eigenschaften kann es notwendig sein, einige isotrope Materialeigenschaften zu definieren.

Die folgenden Symbole werden in diesem Abschnitt verwendet:

E_f Elastizitätsmodul des Fasermaterials

E_m Elastizitätsmodul des Matrixmaterials

G_f Scher-Elastizitätsmodul des Fasermaterials

G_m Scher-Elastizitätsmodul des Matrixmaterials

μ_f Querdehnung des Fasermaterials

μ_m Querdehnung des Matrixmaterials

V_f Bruchteil des Gesamtvolumens des Fasermaterials

V_m Bruchteil des Gesamtvolumens des Matrixmaterials (=1-V_f)

Elastische Eigenschaften

• Elastizitätsmodul, lokale Achse 1 (E1): Das Elastizitätsmodul für die lokale Achse 1 ist die Neigung der Spannungs-/Dehnungskurve der lokalen Achse 1 eines Materials bis zur maximalen Proportionalität. Dies wird auch als Elastizitätsmodul der lokalen Achse 1 bezeichnet. Für einen Faserverbundwerkstoff kann außerdem die folgende Gleichung verwendet werden: E1 = V_f*E_f + V_m*E_m, wobei die Eigenschaften in der Richtung der lokalen Achse 1 liegen. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar und für alle Strukturanalysetypen erforderlich.
• Elastizitätsmodul, lokale Achse 2 (E2): Das Elastizitätsmodul für die lokale Achse 2 ist die Neigung der Spannungs-/Dehnungskurve der lokalen Achse 2 eines Materials bis zur maximalen Proportionalität. Dies wird auch als Elastizitätsmodul der lokalen Achse 2 bezeichnet. Für einen Faserverbundwerkstoff kann außerdem die folgende Gleichung verwendet werden: E2 = V_f*E_f + V_m*E_m, wobei die Eigenschaften in der Richtung der lokalen Achse 2 liegen. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar und für alle Strukturanalysetypen erforderlich.
• Poissonsche Konstante - Lokaler Layer 12 (Hauptebene) (μ₁₂): Dies wird ermittelt, indem Sie die negative Querdehnung des lokalen Layers 12 durch die axiale Dehnung in der lotrechten Richtung zum lokalen Layer 12 für ein axial belastetes Element teilen. (μ₁₂ = -Dehnung in Richtung 2 / Dehnung in Richtung 1). Typische Werte für die Poissonsche Konstante liegen im Bereich von 0.0 bis 0.5. Für ein Faserverbundwerkstoff kann die folgende Gleichung verwendet werden: μ₁₂ = V_f x μ _f + V_m x μ_m, wobei die Eigenschaften in der Ebene 12 gemessen werden. Die Querdehnung für den lokalen Layer 12 kann als Hauptquerdehnung bezeichnet werden. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar und für alle Strukturanalysetypen erforderlich.
• Die Poissonsche Konstante - Lokale Ebene 21 (Neben) (μ₂₁): Für einen Faserverbundwerkstoff (orthotropes Material) kann die folgende Gleichung verwendet werden: μ₂₁ =μ₁₂ x (E2/E1). Die Querdehnung für die lokale Ebene 21 kann als Nebenquerdehnung bezeichnet werden. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar und für alle Strukturanalysetypen erforderlich.
• Der Wärmekoeffizient der Ausdehnung für die lokale Achse 1 ist eine Eigenschaft auf der Grundlage der Verdichtung und Ausdehnung des Materials. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar und für alle Strukturanalysetypen erforderlich, die thermische Lasten umfassen.
• Der Wärmekoeffizient der Ausdehnung für die lokale Achse 2 ist eine Eigenschaft auf der Grundlage der Verdichtung und Ausdehnung des Materials. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar und für alle Strukturanalysetypen erforderlich, die thermische Lasten umfassen.
• Das Scherelastizitätsmodul, lokaler Layer 12 (G12): (in der Ebene des Elements) ist die Neigung der Scherspannung im Vergleich zur Scherdehnung des Layers 12 eines Materials bis zur maximalen Proportionalität. Es wird auch als Schubelastizitätsmodul bezeichnet. Für einen Faserverbundwerkstoff kann die folgende Gleichung verwendet werden: G₁₂ = (G_fxG_m) / (V_mxG_f + G_mxV_f). Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar und für alle Strukturanalysetypen erforderlich.
• Das Scherelastizitätsmodul, lokale Ebene 13: (senkrecht zum Element) ist die Neigung der Scherspannung im Vergleich zur Scherdehnung der Ebene 13 eines Materials bis zur maximalen Proportionalität. Es wird auch als Schubelastizitätsmodul bezeichnet. Diese Eigenschaft ist nur für dicke Verbundelemente anwendbar und für alle Strukturanalysetypen erforderlich.
• Das Scherelastizitätsmodul, lokale Ebene 23: (senkrecht zum Element) ist die Neigung der Scherspannung im Vergleich zur Scherdehnung der Ebene 23 eines Materials bis zur maximalen Proportionalität. Es wird auch als Schubelastizitätsmodul bezeichnet. Diese Eigenschaft ist nur für dicke Verbundelemente anwendbar und für alle Strukturanalysetypen erforderlich.

Zulässige Spannungen

Zulässige Spannungen sind erforderlich, wenn Tsai-Wu- oder maximale Spannungsfehlerkriterien angegeben sind. Informationen zum Auswählen der Fehlerkriterien und zu den Gleichungen, die die Fehler steuern, finden Sie auf den Seiten Dicke Verbundwerkstoffelemente und Dünne Verbundwerkstoffelemente.

• Die zulässige Druckspannung der lokalen Achse 1 (X_c): ist eine Materialeigenschaft, die für verschiedene Fehlerkriterien in einer Verbundelement-Analyse verwendet wird. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar. Es muss ein positiver Wert eingegeben werden.
• Die zulässige Zugspannung der lokalen Achse 1 (X_t): ist eine Materialeigenschaft, die für verschiedene Fehlerkriterien in einer Verbundelement-Analyse verwendet wird. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar.
• Die zulässige Druckspannung der lokalen Achse 2 (Y_c): ist eine Materialeigenschaft, die für verschiedene Fehlerkriterien in einer Verbundelement-Analyse verwendet wird. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar. Geben Sie einen positiven Wert ein.
• Die zulässige Zugspannung der lokalen Achse 2 (Y_t): ist eine Materialeigenschaft, die für verschiedene Fehlerkriterien in einer Verbundelement-Analyse verwendet wird. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar.
• Scherspannung der lokalen Ebene 12: Die zulässige Scherspannung der lokalen Ebene 12 ist eine Materialeigenschaft, die für verschiedene Fehlerkriterien in einer Verbundelement-Analyse verwendet wird. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar.
• Spannungsinteraktion F12 (Tsai Wu) Die Spannungsinteraktion F12 ist eine Fehlerkriterieneigenschaft, die nur für die Tsai-Wu-Fehlertheorie verwendet wird. Sie ergibt sich aus biaxialen Tests. Die folgende Bedingung muss erfüllt sein, um numerische Stabilität zu erreichen: .
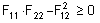• Kernbrechung (Zc): Beim Biegen einer dünnen Schale wirkt auf eine Fläche Spannung und auf die andere Fläche Druck. Die vertikalen Komponenten dieser beiden Kräfte (oben und unten) führen zum Bruch der Kernschicht (Lamina). Der zulässige Wert für die Kernbrechung ist die zulässige Spannung, die auftritt, bevor das Kernmaterial bricht. Dies gilt nur für die maximale Spannungsfehlertheorie und nur für dicke Verbundelemente. Geben Sie einen positiven Wert ein.
• Die Zulässige Querschubspannung in Ebene 13 (S₁₃): (senkrecht zum Element) ist eine Materialeigenschaft, die für verschiedene Fehlerkriterien in einer Verbundelement-Analyse verwendet wird. Dies gilt nur für die maximale Spannungsfehlertheorie und nur für dicke Verbundelemente.
• Die Zulässige Querschubspannung in Ebene 23 (S₂₃): (senkrecht zum Element) ist eine Materialeigenschaft, die für verschiedene Fehlerkriterien in einer Verbundelement-Analyse verwendet wird. Dies gilt nur für die maximale Spannungsfehlertheorie und nur für dicke Verbundelemente.

Zulässige Dehnungen

Zulässige Dehnungen sind erforderlich, wenn maximale Dehnungsfehlerkriterien angegeben sind. Informationen zum Auswählen der Fehlerkriterien und zu den Gleichungen, die die Fehler steuern, finden Sie auf den Seiten Dicke Verbundwerkstoffelemente und Dünne Verbundwerkstoffelemente.

• Die zulässige Druckbeanspruchung der lokalen Achse 1 (T_1c) ist eine Materialeigenschaft, die für verschiedene Fehlerkriterien in einer Verbundelement-Analyse verwendet wird. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar. Geben Sie einen positiven Wert ein.
• Die zulässige Zugdehnung der lokalen Achse 1 (T_1t) ist eine Materialeigenschaft, die für verschiedene Fehlerkriterien in einer Verbundelement-Analyse verwendet wird. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar.
• Die zulässige Druckbeanspruchung der lokalen Achse 2 (T_2c) ist eine Materialeigenschaft, die für verschiedene Fehlerkriterien in einer Verbundelement-Analyse verwendet wird. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar. Geben Sie einen positiven Wert ein.
• Die zulässige Zugdehnung der lokalen Achse 2 (T_2t) ist eine Materialeigenschaft, die für verschiedene Fehlerkriterien in einer Verbundelement-Analyse verwendet wird. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar.
• Scherdehnung der lokalen Ebene 12: Die zulässige Scherdehnung der lokalen Ebene 12 ist eine Materialeigenschaft, die für verschiedene Fehlerkriterien in einer Verbundelement-Analyse verwendet wird. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar.

Biegesteuerung

Die Biegeeigenschaften werden standardmäßig aus den elastischen Eigenschaften berechnet. Um bestimmte Werte für die Biegeeigenschaften zu verwenden, aktivieren Sie das Kontrollkästchen Biegemodul, und geben Sie die folgenden Eigenschaften ein.

• Biegemodul, lokale Achse 1: Das Biegemodul der lokalen Achse 1 ist die Neigung der Moment/Krümmungskurve in der Richtung der lokalen Achse 1 unterhalb der maximalen Proportionalität. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar.
• Biegemodul, lokale Achse 2: Das Biegemodul der lokalen Achse 2 ist die Neigung der Moment/Krümmungskurve in der Richtung der lokalen Achse 2 unterhalb der maximalen Proportionalität. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar.
• Die Biegequerdehnung, lokaler Layer 12: ist das Verhältnis der Krümmung in der Richtung der lokalen Achse 1 zur Krümmung in der Richtung der lokalen Achse 2. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar.
• Das Torsionsträgheitsmoment, lokaler Layer 12: ist vergleichbar mit dem Schermodul. Wenn kein Wert angegeben ist, wird ein Wert mit dem Biegemodul und der Biegequerdehnung berechnet. Diese Eigenschaft ist für beide Arten von Verbundelementen anwendbar.