Le concept du chaos contrôlé est essentiel dans un système de particules. Pour appliquer le chaos à un opérateur de données, utilisez le sous-opérateur Aléatoire. Ce sous-opérateur génère des valeurs scalaires et vectorielles aléatoires selon divers algorithmes décrits dans cette section.
Examen des exemples aléatoires
Commençons par un exemple de positionnement chaotique des particules autour d'un objet de référence : reportez-vous au fichier inclus RandomPositioning.max .
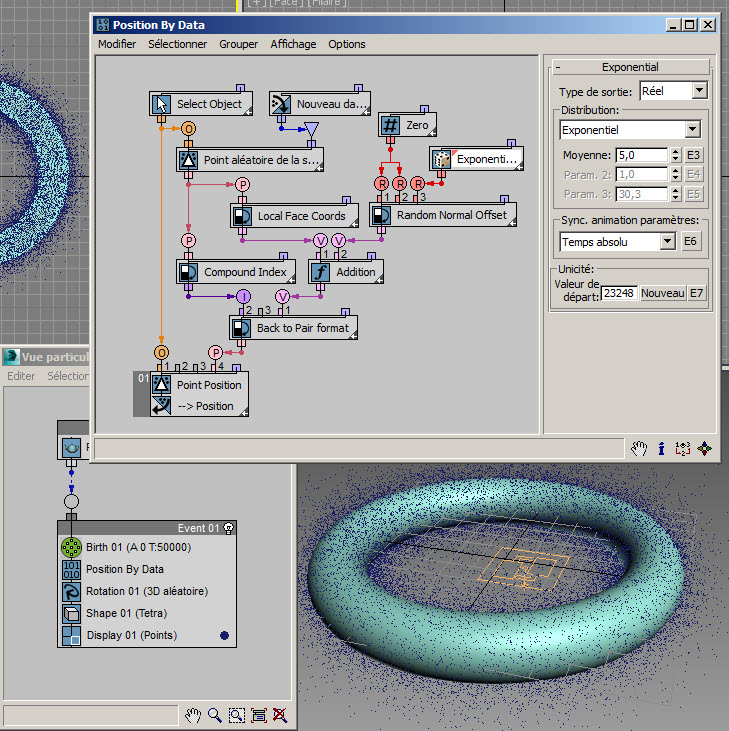
Dans le flux de données illustré ci-dessus, le sous-opérateur Géométrie (1.) répartit des points aléatoires uniformément sur la surface d'un objet de référence. La sortie de données de type Paire est ensuite subdivisée entre deux sous-opérateurs Convertir : Coordonnées locales des faces (2.) et Index composé (3.) qui inclut l'index de face où se situe un point aléatoire.
Pour obtenir une distribution souhaitable des particules dans le volume autour de l'objet de référence, nous devons "soulever" les particules de la surface ; cela peut se faire en modifiant le composant Z du vecteur de coordonnées locales des faces. Le composant Z correspond à la distance à partir de la face dans la direction de la normale de la face.
Un sous-opérateur Aléatoire (4.) peut être utilisé pour définir l'ampleur du soulèvement. Dans cet exemple, nous avons utilisé une distribution exponentielle, qui est positive et plus dense autour de zéro. Davantage de particules sont ainsi placées près de la surface et la densité diminue progressivement avec la distance par rapport à la surface.
Les coordonnées locales des faces modifiées et l'index composé sont ensuite reconvertis en données de type Paire, utilisées dans le sous-opérateur Géométrie (5.) pour calculer la position des particules dans le système de coordonnées Univers.
Examinons le paramètre distribution du sous-opérateur aléatoire. Ce paramètre permet de définir le type de fonction aléatoire utilisée dans le sous-opérateur. Le type de fonction varie aussi selon le type de données que le sous-opérateur Aléatoire produit.
Pour la présentation qui suit, ouvrez le fichier de scène inclus RandomTemplate.max , qui permet de tester différentes fonctions de distribution.
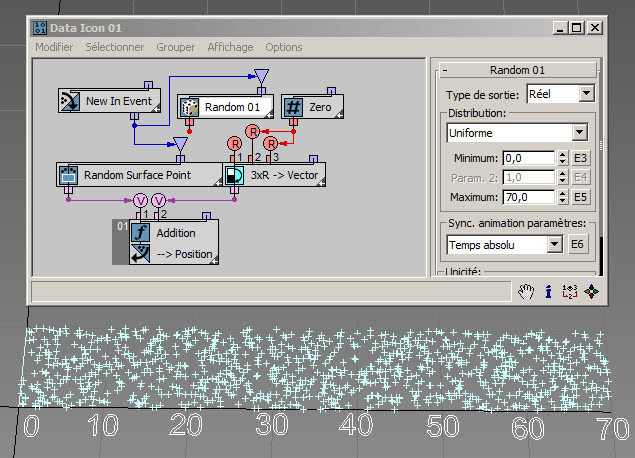
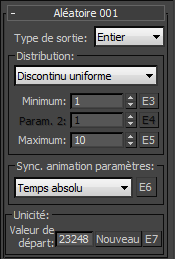
Vous allez commencer par une forme simple de distribution : le type Discontinu uniforme. C'est le seul type disponible si le type de données défini dans le sous-opérateur Aléatoire est Entier. Discontinu est l'opposé de continu. Le sous-opérateur Aléatoire génère des données de type Entier (c'est en ce sens qu'il est discontinu) uniformément réparties entre les valeurs minimale et maximale définies dans l'interface utilisateur. Dans l'exemple suivant ( RandomTemplate01.max ), les valeurs maximale et minimale sont définies sur 0 et 30. Par conséquent, vous pouvez voir que les positions des particules sont réparties le long des lignes d'ordonnées X : 0, 1, 2, 3, etc. jusqu'à 30. Pour des informations théoriques sur la distribution discontinue, consultez Loi uniforme discrète.
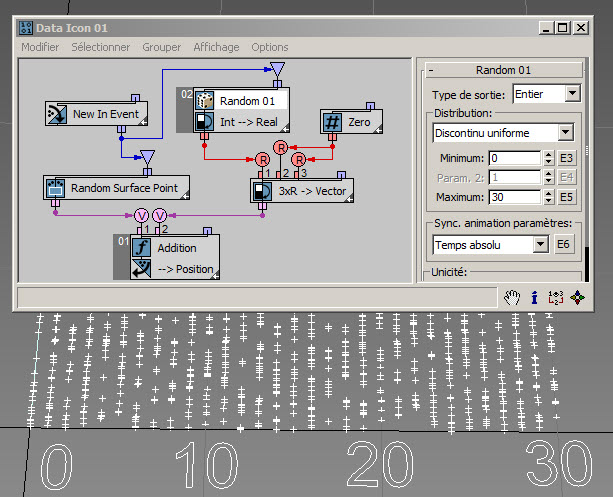
La sortie en données réelles permet la plus grande variété de types de distribution disponibles.
La distribution uniforme est très similaire à la distribution Discontinu uniforme : des valeurs minimale et maximale définissent la plage de distribution, mais les valeurs sont réparties de façon continue sur l'intervalle. Pour en savoir plus, consultez Loi uniforme continue.
L'option de distribution exponentielle est couramment utilisée dans l'ingénierie de fiabilité. Elle peut être utilisée pour simuler le comportement d'unités présentant un taux de défaillance constant réellement aléatoire. Un autre exemple de distribution exponentielle est la distribution des durées de vie individuelles de particules instables dans la désintégration radioactive.
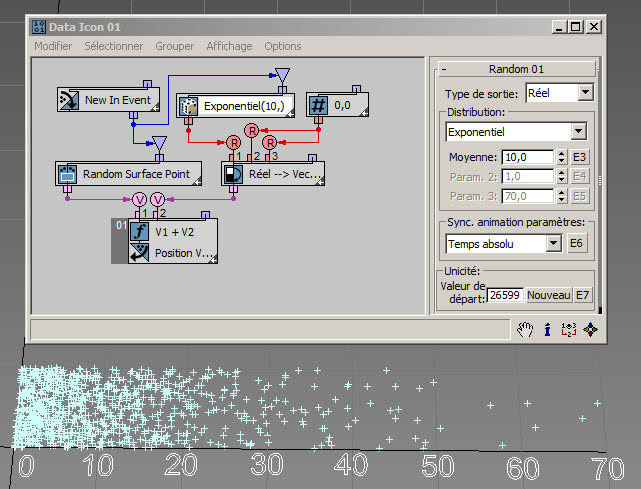
La distribution exponentielle génère des valeurs positives uniquement. Environ la moitié des valeurs générées est inférieure au paramètre Moyenne et davantage de valeurs sont générées à mesure que l'on approche zéro. Une valeur générée peut être arbitrairement grande. Toutefois, plus la valeur est grande, plus sa probabilité est faible. Dans cet exemple ( RandomTemplate02.max ), la moyenne est de 10. La majorité des valeurs générées sont donc comprises entre 0 et 70. Pour en savoir plus, consultez Loi exponentielle.
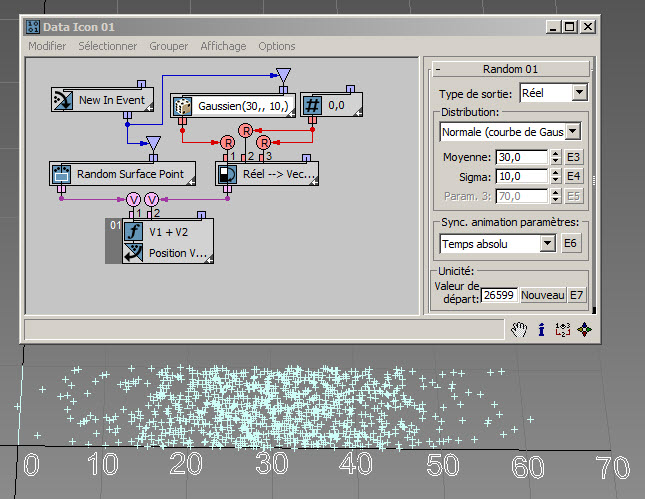
La distribution Normale (courbe de Gauss) décrit la distribution d'erreurs d'observation aléatoires indépendantes. Une distribution normale ou quasi-normale s'observe par exemple dans la température du corps, les pointures, les diamètres des arbres, etc. Un schéma de distribution normale prend la forme d'une courbe symétrique en forme de cloche. Le paramètre Moyenne définit la valeur moyenne des valeurs générées (le centre de la courbe), tandis que le paramètre Sigma définit l'écart maximal des valeurs générées par rapport à la valeur moyenne. La plupart des valeurs (99,7 %) sont générées à l'intérieur de l'intervalle de décalage 3 Sigma [Moyenne3*Sigma, Moyenne + 3*Sigma]. Dans l'exemple suivant ( RandomTemplate03.max ), la moyenne est de 30, tandis que le sigma est de 10. La majorité des valeurs générées sont donc comprises entre 0 et 60. Une distribution normale génère des valeurs positives et négatives. Une valeur générée peut être arbitrairement grande. Toutefois, plus la valeur est grande, plus sa probabilité est faible (voir la règle des 3 Sigma, ci-dessus). Pour en savoir plus, consultez Loi normale.
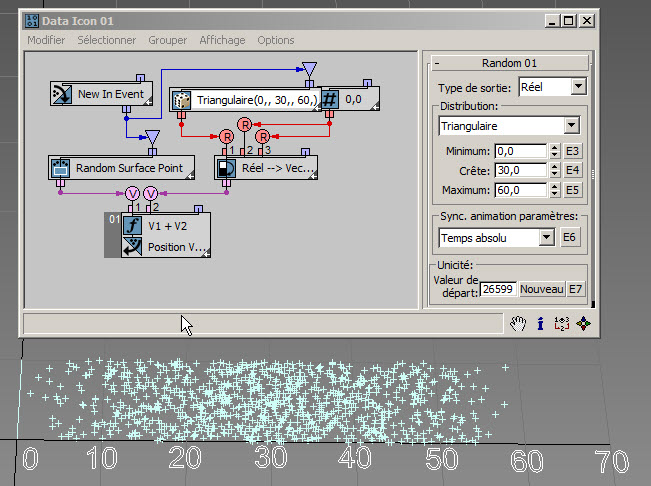
La distribution triangulaire est une façon simpliste de décrire un phénomène aléatoire tendant vers une valeur crête et limité à un intervalle défini par des valeurs minimale et maximale. Dans cet exemple ( RandomTemplate04.max ), la distribution triangulaire émule la distribution normale de l'exemple précédent. Pour en savoir plus, consultez Loi triangulaire.
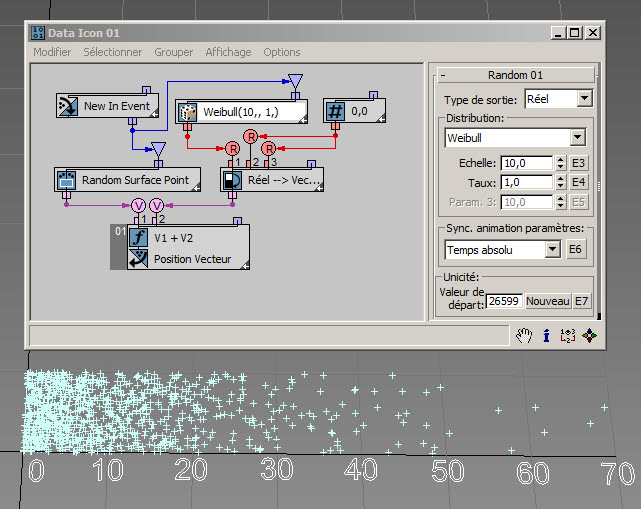
La méthode de distribution Weibull étend la distribution exponentielle aux événements qui ne sont pas strictement aléatoires ; cette distribution est couramment utilisée dans la modélisation de fiabilité et de durée de vie avec vieillissement. Dans cet exemple ( RandomTemplate05.max ), le taux est égal à 1. Dans ce cas, la distribution Weibull est égale à la distribution exponentielle avec le paramètre Moyenne comme paramètre Echelle Weibull.
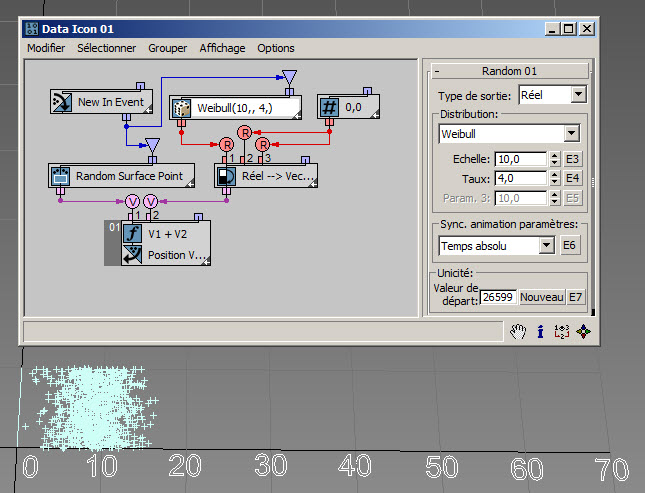
Vous pouvez utiliser la distribution Weibull pour modéliser le temps jusqu'à la défaillance d'un appareil technique. Si le taux de défaillance de l'appareil diminue avec le temps, définissez Taux < 1. Si le taux de défaillance de l'appareil augmente avec le temps, définissez Taux > 1. La distribution Weibull permet également de modéliser la distribution des vitesses de vent à un emplacement donné sur la Terre : chaque emplacement est caractérisé par un Taux et une Echelle particuliers. Dans cet exemple ( RandomTemplate06.max ), le taux de défaillance est égal à 4 et l'échelle est de 10. La majorité des valeurs aléatoires générées sont donc comprises entre 3 et 15. Pour en savoir plus, consultez Loi de Weibull.
Vous pouvez utiliser les options Bruit R, Bruit V, Bruit V+T, Turbulence V et Turbulence V+T pour générer des valeurs pseudo-aléatoires de type bruit à partir de données réelles, vectorielles et/ou de temps. Le paramètre Echelle définit le taux de dépendance entre les données d'entrée et de sortie. Des valeurs élevées produisent un bruit plus doux, tandis que de faibles valeurs augmentent le crénelage du bruit. Le paramètre Portée détermine la grandeur des valeurs produites.
Les options Turbulence ont un paramètre Itérations qui définit le nombre d'itérations (octaves) utilisé pour générer le bruit fractal. Des itérations plus petites donnent une sortie plus lisse. Le paramètre Itérations est compris entre 1.0 et 10.0. Les options Bruit génèrent des valeurs positives et négatives ; les options Turbulence génèrent des valeurs positives.
Cet exemple ( RandomTemplate07.max ) utilise la coordonnée X aléatoire d'une particule pour générer des valeurs aléatoires de type bruit pour la coordonnée Y :
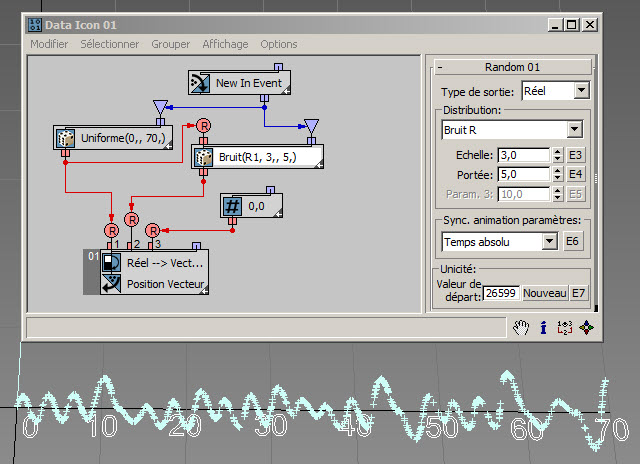
Dans l'exemple suivant ( RandomTemplate08.max ), les particules sont placées de manière aléatoire sur la surface de l'icône de l'opérateur de données, puis la position est utilisée comme entrée du sous-opérateur Aléatoire avec l'option Bruit V. Les données de sortie sont utilisées pour définir la hauteur des particules (axe Z).
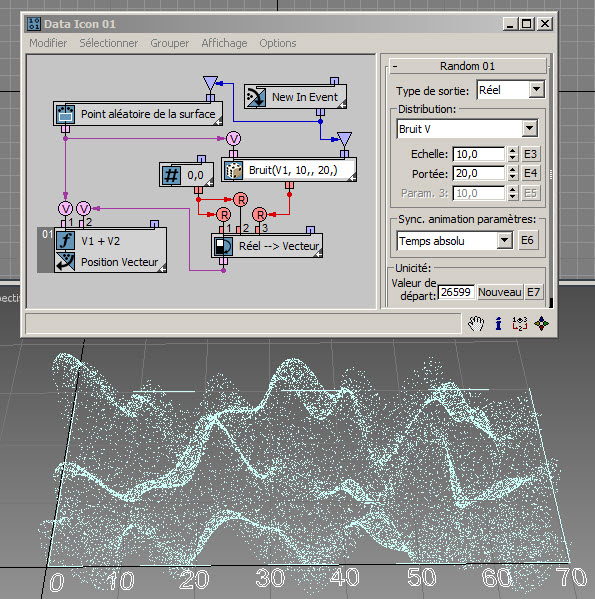
En reliant le temps absolu à l'entrée Temps des options ...+T, il est possible d'animer facilement le bruit généré, comme illustré dans cet exemple ( RandomTemplate09.max ) :
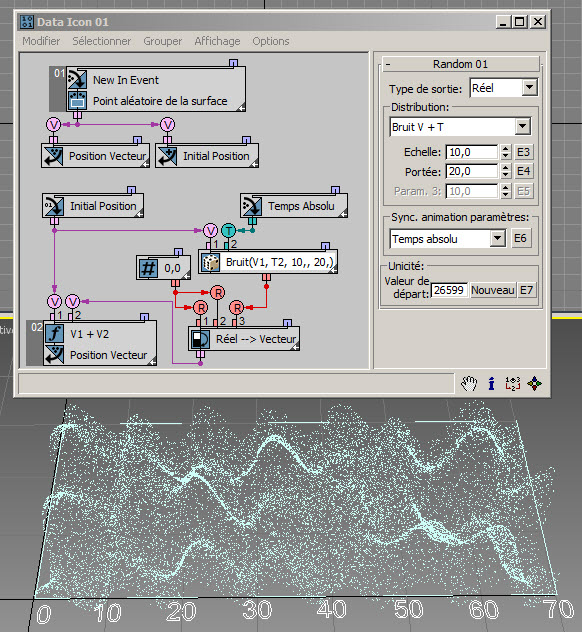
Les options Turbulence sont très similaires aux options Bruit. Vous devez juste définir le paramètre Itérations, comme illustré dans cet exemple ( RandomTemplate10.max ).
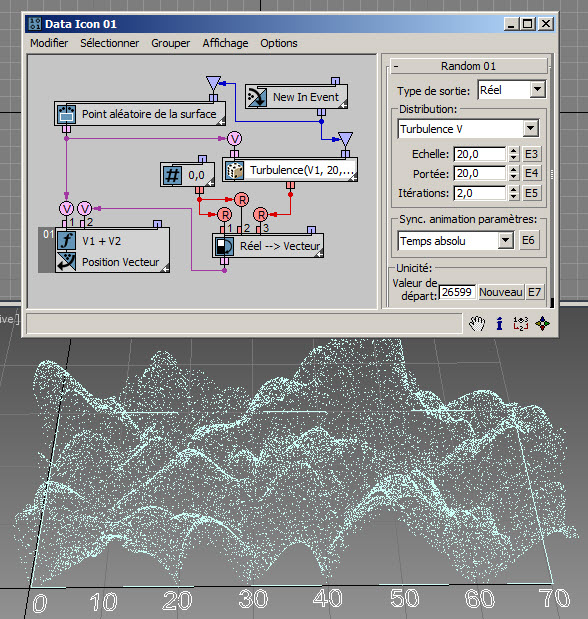
... et dans cet exemple ( RandomTemplate11.max ) :
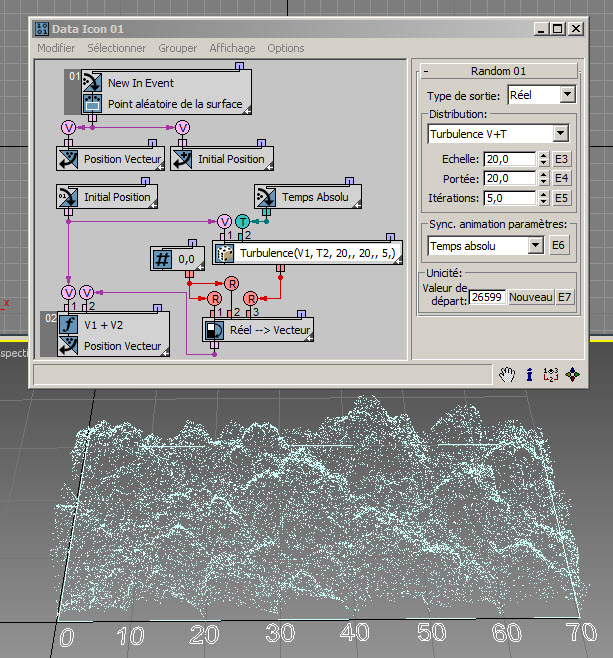
La dernière catégorie d'options de distribution génère des données vectorielles.
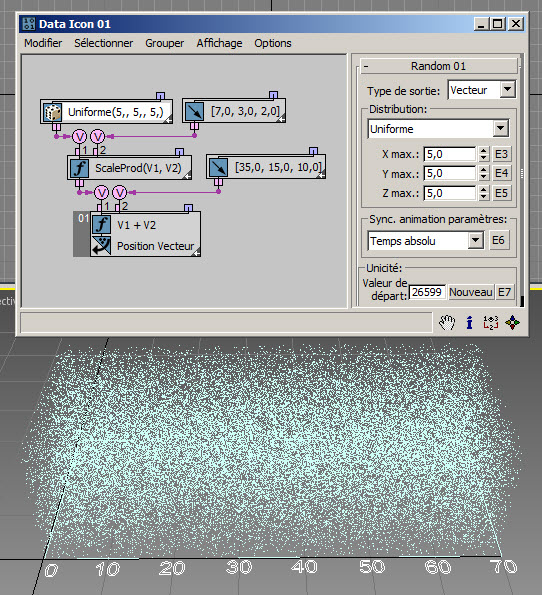
L'option Distribution uniforme génère des valeurs vectorielles aléatoires à l'intérieur d'une boîte englobante avec des limites [-Max X, Max X] pour le composant X, [-Max Y, Max Y] pour le composant Y et [-Max Z, Max Z] pour le composant Z. Avec un nombre suffisant de particules, la boîte englobante peut être remplie de points vectoriels aléatoires ( RandomTemplate12.max ) :
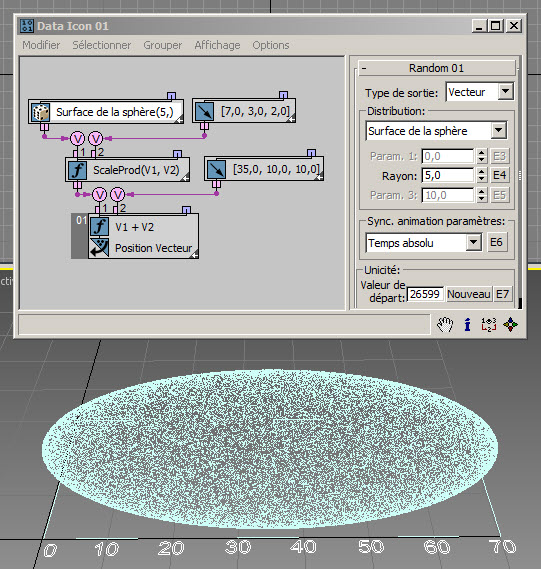
L'option Surface de la sphère peut être utilisée pour placer des particules sur la surface d'une sphère. Toutefois, son utilisation la plus courante est la génération d'un vecteur de direction aléatoire. Dans ce cas, le paramètre Rayon définit la longueur du vecteur ( RandomTemplate13.max ) :
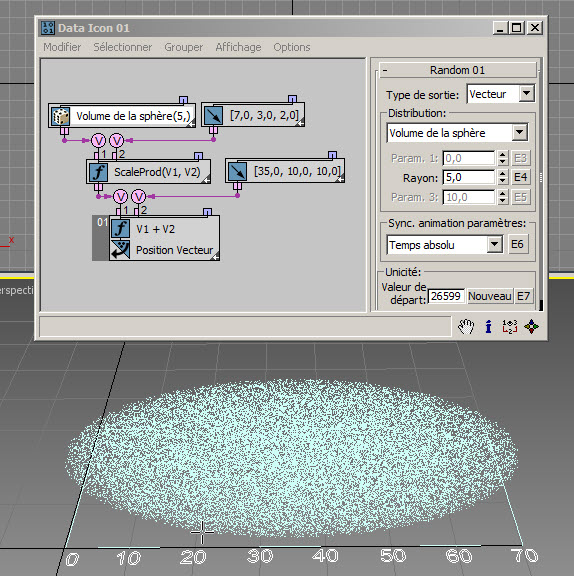
Vous pouvez aussi choisir de remplir tout le volume de la sphère avec des points aléatoires ( RandomTemplate14.max ) :
Vous pouvez aussi utiliser l'option Normale (courbe de Gauss) pour remplir le volume d'une sphère, mais, avec cette option, il n'y a pas de limite de contour de la sphère : davantage de points sont générés vers le centre de la sphère et leur densité diminue en s'éloignant du centre. La même règle 3 Sigma que ci-dessus peut être appliquée ici : 99,7 % des points sont générés à l'intérieur d'une sphère d'un rayon égal à 3*Sigma ( RandomTemplate15.max ).
Les options Bruit V, Bruit V+T, Turbulence V et Turbulence V+T sont similaires aux options de données réelles du même nom, si ce n'est qu'elles génèrent des données vectorielles. Pour illustrer les données produites, nous pouvons les relier au canal Vitesse dans l'étape Après et définir la vitesse sur zéro dans l'étape Avant. De cette façon, les particules ne vont nulle part, mais nous pouvons tracer la sortie sous la forme de lignes de vitesse. Dans cet exemple ( RandomTemplate16.max ), les particules sont placées de manière aléatoire dans un rectangle, puis leur position est utilisée comme entrée du sous-opérateur Aléatoire avec l'option Bruit V :
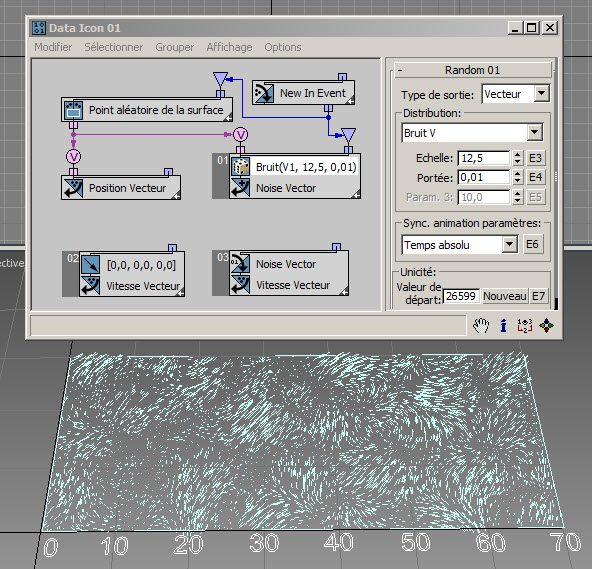
Et voici RandomTemplate17.max , la même configuration, mais avec l'option Bruit V+T. Nous utilisons le temps courant comme entrée du sous-opérateur Aléatoire afin d'animer la sortie Bruit :
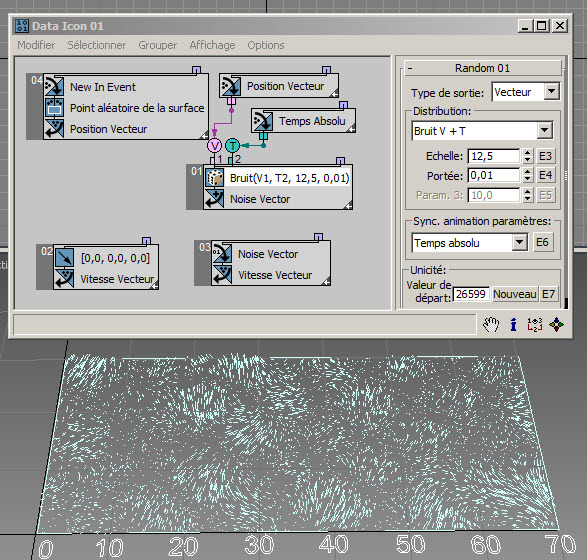
Nous pouvons relier la sortie du sous-opérateur Aléatoire au canal Vitesse et utiliser le canal Position en entrée du même sous-opérateur : cela permet de simuler les turbulences du vent. Voici l'image 98 du fichier de scène RandomTemplate18.max :
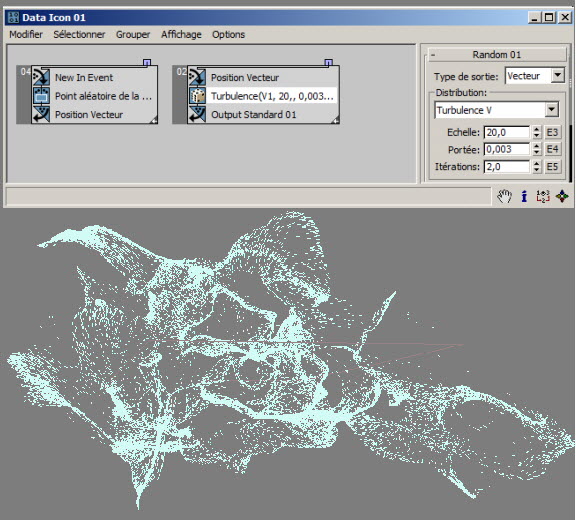
Interface
- Type de sortie
- Sélectionnez le type de données pour la sortie :
- Entier
- Réel
- Vecteur
Le paramètre Type de sortie détermine les paramètres disponibles dans la zone Distribution.
Zone Distribution
Le contenu de la liste déroulante Distribution est déterminé par le type de sortie choisi. La distribution choisie détermine à son tour les autres paramètres de la zone Distribution.
Reportez-vous à la section précédente pour plus d'informations sur les options de distribution et les paramètres y afférents.
- Synchronisation animation paramètres
- Lorsque vous animez les paramètres du sous-opérateur, le logiciel peut commencer par appliquer cette animation à toutes les particules depuis la première image de l'animation ou de l'événement courant, ou à chaque particule en fonction de son âge. Les options disponibles sont les suivantes :
- Durée absoluetoutes les clés définies pour les paramètres sont appliquées aux images réelles pour lesquelles elles sont configurées.
- Durée événementtoutes les clés définies pour les paramètres sont appliquées à chaque particule au niveau de l'image où elle entre pour la première fois dans l'événement.
- Age particuletoutes les clés définies pour les paramètres sont appliquées aux images correspondantes relatives à l'existence de chaque particule.
- Durée de vie des particules : met à l'échelle/mappe l'animation des paramètres par rapport à la durée de vie des particules. Par exemple, si la valeur d'un paramètre est animée de 5 à 20 sur les images 0 à 100, ce paramètre a la valeur 5 lorsque la particule est émise et 20 lorsque la particule disparaît. De cette façon, vous pouvez, par exemple, définir le changement d'échelle d'une particule sur sa durée de vie.
Pour que cette option fonctionne correctement, il doit y avoir dans le flux un opérateur Supprimer défini sur Selon l'âge de la particule afin de définir la durée de vie de la particule.
- Saisie de données de temps : ajoute une entrée Temps au sous-opérateur, à laquelle vous pouvez relier tout autre sous-opérateur produisant des données au format Temps.
- E6
- Ajoute une entrée de données de type Egal pour permettre à l'utilisateur de contrôler la valeur Sync. animation. Cette entrée ne peut recevoir des données que d'un sous-opérateur Paramètre défini sur un Type=Sync. animation.
- Unicité
- Permet de faire varier la séquence de nombres aléatoires générée par le sous-opérateur Aléatoire. Entrez une valeur de départ manuellement ou cliquez sur Nouveau pour laisser le logiciel générer une valeur de départ.
- E7
- Ajoute une entrée de données de type Egal pour permettre à l'utilisateur de contrôler la valeur Unicité. Cette entrée ne peut recevoir des données que d'un sous-opérateur Paramètre défini sur un Type=unicité.