それでは、大ノッチ試験用断片に対して行ったように、SDV1 を調べて十字型の損傷を評価しましょう。また、破損が伝播するにつれて要素がモデルから削除される様子を確認することもできます。
織物材料の場合、SDV1 の範囲が 1.0 から 3.0 になることを思い出してください。ただし、1.0 から 3.0 までの離散値は、異なる損傷状態を表します。詳細は、「付録 C」を参照してください。
- ジョブが完了したら、メイン ツールバーからをクリックして、 Tutorial_6_PW_Abaqus.odb を開きます。これにより、出力データベース ファイルが開き、可視化モジュールに切り替わります。
- [Field Output]ダイアログ ボックスの変数のドロップダウン リストから[SDV1]を選択します。

- [Deformation Scale Factor]を調整し()、[Deformation Scale Factor]フィールドに 1 の値を入力します。[OK]をクリックします。
- 既定のコンター タイプは[Banded]に設定されていますが、SDV1 の表示には[Quilt]タイプの方が効果的です。[Banded]から[Quilt]に切り替えるには、メイン ツールバーからを選択し、[Contour Type]として[Quilt]を選択します。プロットは、下に示したような内容になるはずです。通常、メッシュのバリエーションによって、若干の違いが出ます。
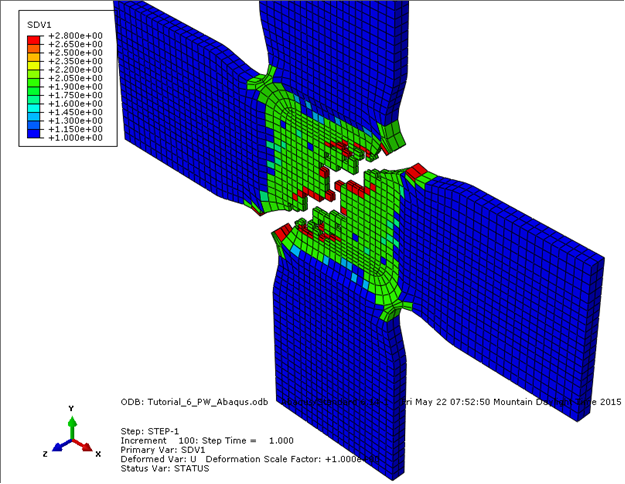
視覚的には、このモデルで要素の削除の効果をはっきりと確認することができます。要素の削除では、非常に簡単に破損を識別できます。
この十字型サンプルの荷重-変位曲線をプロットしていれば、要素の削除を使用した場合と使用しなかった場合の応答が非常に類似していることがわかったでしょう。十字型では、破損の多くは数回の増分内で発生するため、これは驚くべきことではありません。
損傷が何回もの増分に渡って徐々に伝播するようなモデルの場合は、要素の削除を使用した場合としなかった場合の応答に大きな違いが出ることでしょう。このようなケースでは、要素の削除をアクティブにした方が、物理的に妥当な結果となるようです。これは、材料を非常に低い剛性に劣化させることが困難であるような織物材料の場合に特に当てはまります。要素は、削除されるまではモデルのひずみエネルギーに貢献し続けるために、結果として、損傷の伝播に影響を与えることを思い出してください。これが原因で、破損後の剛性が予想よりも高くなる場合があります。