MCT 基準は、多重連続体理論39,40(MCT)に基づいています。多重連続体の概念は、代表体積要素(RVE)内に共存する明らかに異なる材料を反映するために、連続体の観念を拡張します。大幅に異なる材料特性を持つ 2 つ以上の明確に識別可能な構成要素がある場合に、このような拡張は当然です。したがって、一方向繊維強化複合材料は、適切に選択した複合材料の RVE 内に共存する 2 つの相互作用する連続体(繊維連続体と母材連続体)と見なすことができます。
従来の連続体力学(繊維強化複合構造に適用)では、さまざまな複合材料の平均数量(応力、ひずみなど)間の関係を開発することに焦点が当てられていました。多重連続体理論(MCT)は、次の 2 つの問題にさらに焦点を拡大することで、従来の連続体力学を補強します: 1) さまざまな構成の平均数量間の関係の開発、および 2) 複合材料の平均数量と構成の平均数量をリンクする関係の開発。
MCT は、複合材料や積層のレベルではなく、繊維および母材レベルの破損を予測します。これはまず、繊維および母材における平均応力状態のボリュームを得ることで行われます。構成応力は、複合材料の応力の関数と複合材料の繊維と母材の剛性です。
MCT 分解
繊維と母材の応力は、次の応力とひずみの分解プロセスによって得られます。最初のステップは、母材のひずみ状態を取得することです。
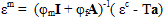
ここで、φf と φm はそれぞれ繊維と母材の体積分率を示します。I は 6x6 の ID マトリックスで、A と a はそれぞれ構成内の平均機械ひずみと平均熱ひずみを示します。次のように定義されます。
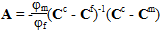
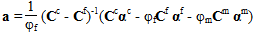
繊維のひずみは次を使用して見つけることができます。
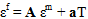
そして、繊維と母材の応力状態は次のようにして計算することができます。
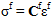
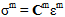
構成応力は、繊維と母材の破損を個別に評価するために使用されます。
MCT 母材構成の破損基準
一方向複合材料における母材構成の破損基準を作成する場合、次のように仮定されます。
- 母材破損は、母材の 6 つの平均応力成分
、
、
、
、
、
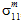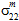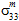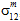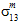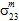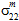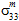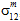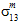のすべてに影響されると仮定されます。 - 母材構成材料は横等方性であると仮定されます。したがって、母材の破損に対して、 と のどちらが影響を与えたかを区別することや、 と のどちらが影響を与えたかを区別することはできません。
- 母材破損の生成における母材の平均垂直応力(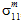、、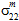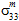)の影響は、垂直応力が引張または圧縮であるかによって異なります。
これらの 4 つの基本的な仮定を使用して、母材破損基準は母材の平均応力の成分の二次関数として表現されます。
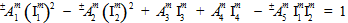
上記の方程式では、数量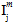 
(j=1,2,3,4) は、母材の平均応力状態の横等方性不変量です。
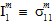
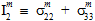
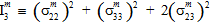
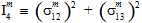
数量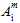 
(i=1,2,3,4,5) は、母材破損基準の係数です。係数 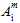の前に上付き文字記号 '±' が付いている場合、関連付けられた母材の平均応力が引張か圧縮のいずれであるかによって 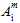の数値が異なることを示しています。したがって、
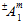は 2 種類の値を表す可能性があります。 実際には、係数 
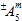には、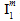
が正または負の値であるか、さらに 
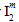が正または負の値であるかによって可能な値が 4 つあります。そのため、母材破損基準には複合材料の測定強度を使用して決定することが必要な調整係数が、全部で 10 種類含まれています。
MCT 繊維構成の破損基準
- 繊維破損は、繊維の平均応力成分
、
、
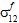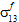によって影響されると仮定されます。 - 繊維破損は、繊維の平均応力成分
、
、
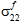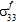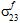には依存しないと仮定されます。 - 繊維破損の生成における の影響は、 が引張または圧縮であるかによって異なります。
- 繊維構成材料は横方向に等方性であると仮定されます。したがって、繊維の破損に対して、 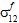と 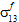のどちらが影響を与えたかを区別することはできません。
これらの 4 つの基本的な仮定を使用して、繊維破損基準fは繊維の平均応力の成分の二次関数として表現されます。
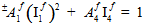
数量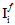 
(i=1,4) は、繊維の平均応力状態の 2 つの横等方性不変量です。
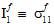
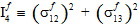
数量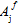 
(j=1,4) は、繊維破損基準の調整係数です。係数 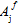の前に上付き文字記号 '±' が付いている場合、関連付けられた繊維の平均応力が引張か圧縮のいずれであるかによって 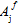の数値が異なることを示しています。したがって、
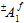は 2 種類の値を表す可能性があります。 そのため、繊維破損基準には複合材料の測定強度を使用して決定することが必要な調整係数が、全部で 3 種類含まれています。