有限要素定式化は、非定常熱伝導式で使用される熱源項の計算に使用します。
電磁現象を記述する式は、「電磁場のモデリング」を参照してください。有限要素定式化は、そのページの方程式(19)の計算に使用されます。
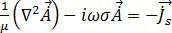(19)
熱源項を取得するには、方程式(21)を使用します。
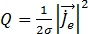(21)
これは方程式(22)を計算するために、既存の冷却ソルバーで使用されます。
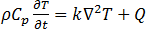(22)
方程式(19)は時間調和的な簡易化された方程式であるため、磁気ベクトル ポテンシャル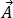 
、および渦電流 
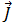は複素数として表す必要があります。
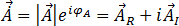(23)
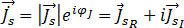(24)
ここで、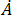
および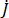 
は解析中の項の直交座標成分で、
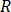および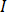 
は複素数の実成分および仮想成分の下付き文字です。
Galerkin 近似が、方程式(19)でベクトルの X、Y、および Z の各成分に対して個別に適用されます。
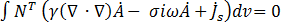(25)
次の形式の 3 つの方程式が作成されます。
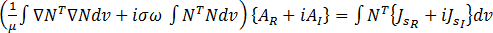(26)
ここで、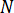
は形状関数を示し、
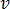は要素の体積を示します。方程式 26 は、磁気ベクトル ポテンシャル 
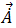の未知の直交座標成分の実成分と仮想成分両方の各四面体要素で計算されます。したがって、 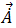には計算する必要がある 6 つの自由度があります。