疲労安全率(FSF)の計算基準は、コンポーネントの予測無限寿命です。サイクル数 N を超える予測無限寿命を得るために、平均応力と変動応力の値を示す線図を作成します。平均応力値と変動応力値により、サイクル数 N (無限寿命)が得られます。このような線図は実験的に作成することができます。ただし、疲労解析では、最大強度、降伏強度、疲労強度などの単調な材料特性に基づいて、このような線図の近似を求めることができます。
疲労解析ウィザードでは、次の 2 種類の FSF 線図を定義できます。
- Goodman 線図
- Haigh 線図(汎用)
FSF は、既定で次に示す Goodman 線図を使用して計算されます。
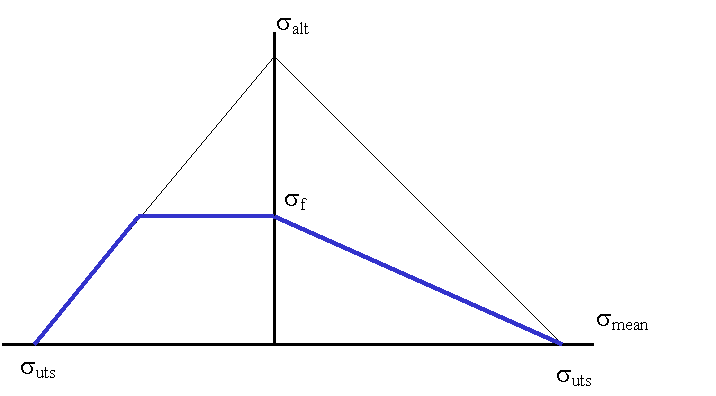
Goodman 線図
汎用 Haigh 線図
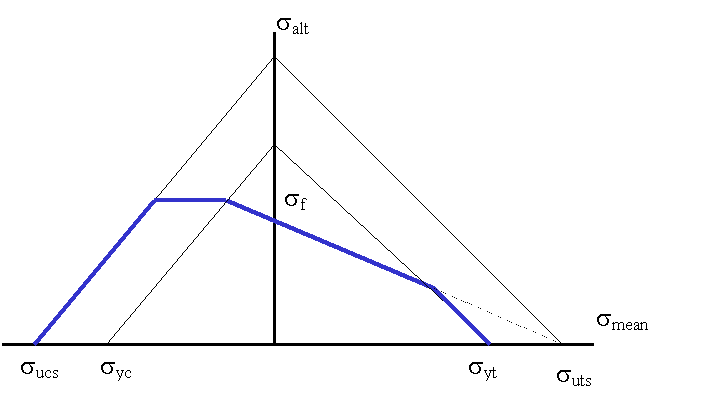
汎用 Haigh 線図は 6 つの点を使用して作成します。各点は、材料 UTS (引張と圧縮)、材料の降伏(引張と圧縮)、および材料の疲労耐久限度の入力データを基に計算されます。Haigh 線図の主要な点が前の図のように定義されます。
FSF の計算
疲労安全率(FSF)の計算基準は、対象の応力サイクルを表す点の比率(平均と変動)、および無限寿命線との交点です。
疲労解析ウィザードでは、無限寿命線との交点を形成する 2 つの標準的な方法で計算を行います。1 つは一定応力比法(constR)、もう 1 つは一定平均法(constM)です。
一定応力比法(constR)
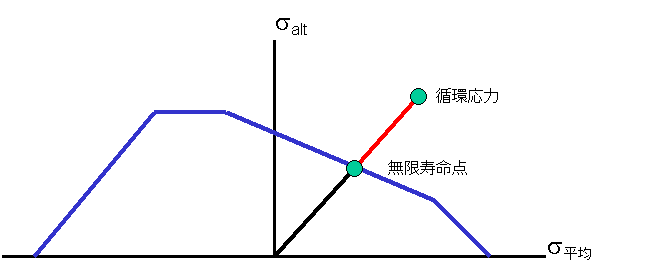
一定応力比法の計算基準は、サイクルにおける応力を無限寿命線にスケーリングする場合、平均応力と変動応力の両方が同じ比率でスケーリングされると仮定する点です。
一定平均法(constM)
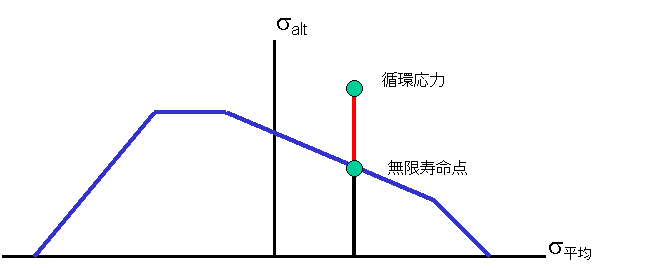
FSF の一定平均法の計算基準は、サイクルにおける応力を無限寿命線にスケーリングする場合、変動応力のみがスケーリングされると仮定する点です。
FSF の計算により、無限寿命に関する安全率が導出されます。この安全率の計算では、(寿命の計算と同様に)応力履歴の構成サイクルの損傷蓄積は生じないと仮定されます。すべてのサイクルの FSF が個別に計算され、最悪の安全率がレポートされます。このレポートでは、最悪のサイクルにおいて材料/コンポーネントから無限寿命を導出できる場合、応力履歴内の後続のサイクルでは、追加的な効果は発生しないと仮定されます。この仮定は、明確な疲労限度を示す鉄鋼材について妥当性があります。ただし、こうした現象を示さない材料に同じ仮定を適用する場合は、注意を払う必要があります。