理論概要

ドイツのエンジニアである Albert は、19世紀初頭に疲労調査を初めて行った人物として知られています。荷重を繰り返し受ける材料はいずれ衰えることが認識されています。しかし、後に疲労として広く認識されることになった最初の現象は、長い間サービスを問題なく提供してきた鉄道車両の車軸における広範囲の破壊でした。

ほとんどの工学的コンポーネントおよび構造では、何らかの周期荷重が発生します。こうしたコンポーネントにおける破壊は、通常小さな亀裂の発生を意味します。このような小さな亀裂は、やがては大きな亀裂となり、破局的な破壊をもたらします。亀裂発生は、材料の単調な降伏応力よりも十分に低い応力レベルで起こり始めます。時間の経過と共に繰り返される損傷は、結果的な破壊が発生するまで蓄積されます。構造破壊の 90% 以上は、疲労損傷の結果引き起こされると言われています。

材料またはコンポーネントが耐えかねる周期荷重の回数を推定する方法として、2 つの基本的アプローチを使用できます。

初期の方法では、19 世紀に Wholer によって初めて収集された材料データを使用していました。この手法では、コンポーネントの応力を S-N 曲線(または Wholder ライン)として知られる経験曲線に関連付け、破壊が発生するまでのサイクル数の推定を取得していました。この手法は、現在でも使用されており、一般的には応力-寿命アプローチと呼ばれます。この手法では、コンポーネントの応力が使用され、材料の弾性領域に応力が残留することが想定されます。したがって、破壊までに 100000+ のサイクルを要する疲労破壊に最も適しています。

2 番目のより近代的な手法では、破壊を予測するために材料ひずみが使用されます。ひずみをサイクルに関連付ける曲線は、応力-寿命アプローチで使用するテストまたは経験式に似たテストまたは経験式から準備できます。この手法を使用する主なメリットは、ひずみ-寿命曲線によってコンポーネントの局部ひずみ状態が表されるため、局部弾性変形を考慮できる点です。これにより、局部降伏が発生する荷重レベルにおける寿命をより正確に予測できます。

疲労解析ウィザードでは、疲労寿命を予測するのにこれら両方の手法が使用されます。

荷重の定義

疲労損傷は、一定期間において構造が繰り返し荷重を受けることによって生じます。疲労破壊を解析するには、適用荷重を定義する必要があります。疲労解析ウィザードでは、2 つの基本的な荷重タイプを設定できます。最もシンプルな形態は、振幅一定高調波です。

この荷重は、応力振幅 sa および平均応力 sm の定義によって完全に記述されます。繰り返しサイクルは単一の高調波期間です。それは図 1 のポイント 1-2-3-4 です。

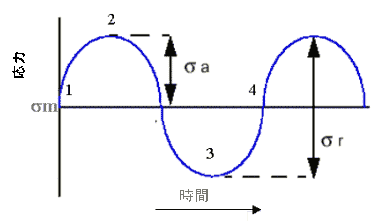
図 1 振幅一定高調波荷重

2 番目のタイプの荷重は、より一般的に使用される振幅可変荷重です。

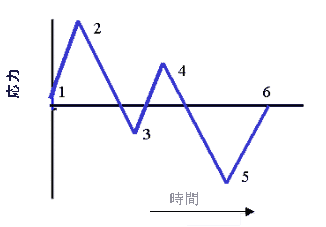
図 2: 振幅可変荷重

振幅可変荷重は、多数の個別の振幅一定サイクルによって構成されます。これら個別のサイクルには、それぞれ異なる振幅および平均値を設定でき、重ね合わせたり、連続させることができます。図 2 は、振幅可変荷重の簡潔な例を示してます。2 つの簡潔なサイクルが示されています。1-2-5-6 によって大きな振幅単一サイクルが形成されています。このサイクルには、より小さいサイクル 3-4-3 が重ね合わされています。したがって、振幅可変荷重は、数多くのより簡潔な振幅一定荷重に分割可能です。分割した振幅一定荷重は、損傷を予測するために疲労解析で使用できます。

振幅可変荷重を疲労計算で使用する場合、「サブサイクル」を抽出する方法を適用する必要があります。疲労解析ウィザードでは、その方法はレインフロー計アルゴリズムによって適用されます。

レインフロー計および疲労損傷

疲労破壊を予測する応力-寿命とひずみ-寿命の両方の手法は、単一サイクルの損傷曲線に基づきます。この損傷曲線では、単一の簡潔なサイクルの応力およびひずみの振幅と繰り返し数が関係付けられます。構造荷重が簡潔な振幅一定タイプである場合、この曲線を直接使用することができます。ただし、振幅可変荷重が定義されている場合、適用荷重の寿命を計算するためにいくつかの手順を実行する必要があります。

まず最初に、荷重履歴に対してピークと谷底の選択が実行されます。このプロセスでは、「反転」ポイントでないすべてのポイントの時間履歴がスキャンおよび破棄されるため、不要データが削減されます。次に、短縮時間履歴が標準レインフロー計アルゴリズムで処理され、個別の単一サイクルが抽出されます。これらの単一サイクルは、単一サイクル損傷曲線で使用され、各サイクルの寿命が計算されます。

時間履歴の各サイクルにおける寿命の計算が終了すると、蓄積損傷または総寿命を決定する方法が必要になります。疲労解析ウィザードでは、適切に文書化された「マイナー則」が使用されます。マイナー則では、荷重履歴全体において蓄積された総損傷は、個別のサイクルの損傷の線形的な合計であると記述されています。

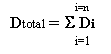
または

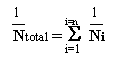
N は繰り返しにおける寿命で、D は損傷です。

応力寿命手法

応力寿命手法では、SN 曲線と呼ばれる単一サイクル損傷曲線が使用されます。この曲線は、応力振幅を破壊までのサイクル数に関連付けます。この手法は、長年に渡って幅広く使用されてきたため、SN 曲線およびその曲線に関連付けられた材料データは容易に入手可能です。曲線で使用する応力値は、曲線で表すデータに依存します。ある意味では、エンジニアが自由に選択できます。単軸バージョンの疲労解析ウィザードでは、応力の方向が一定であると想定されるため、計算に「最悪の絶対原理」の応力が使用されます。

疲労解析ウィザードでは、エンジニアが入力した材料データから NS 曲線が内部的に作成されます。必須のデータは、材料の単調引張強度および「耐久限度」です。

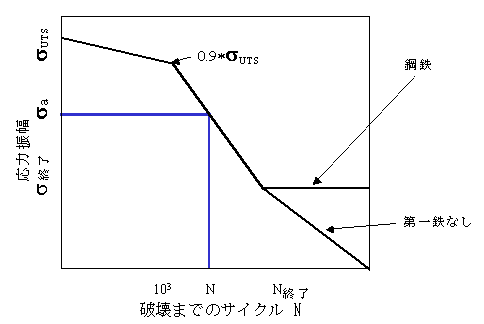
図 3 SN 曲線

SN 曲線には、図 3 に示す形式が使用されます。SN 曲線は、示すとおり、常に両対数尺度上にプロットされます。曲線は、log(N)=1 における単調引張強度 suts から開始されます。次に、通常、1000 サイクルの値までの範囲を直線によって suts の90% の値に近似化します。SN 曲線の主傾斜は、1000 サイクル ポイントから「耐久限度」および送信する等価応力振幅に対応する寿命値まで延びます。耐久限度を超えた動作は、材料が鉄合金または非鉄合金であるかによって異なります。通常、鋼鉄の場合、実際の耐久限度および SN 曲線の平坦化が表れます。その一方で、アルミニウム合金やその他の非鉄合金では、高サイクルにおける SN 曲線の明瞭な平坦化があまり表れません。疲労解析ウィザードでは、これらの 2 つのケースを区別することができます。

平均応力効果

通常、SN 曲線は完全反転テストで使用します。これは、適用応力が等しい引張と圧縮状態間を循環することを意味します。現実の荷重では、サイクル荷重は、通常、非ゼロの平均状態で振動します。この非ゼロ平均状態は、破壊までの寿命に大きな影響を及ぼします。標準 SN データを使用する場合、サイクルにおける平均応力の存在を考慮する方法が必要です。

疲労解析ウィザードでは、「平均なし」、「Gerber」および「Goodman」補正を使用して疲労寿命を計算できます。

応力集中

通常、FE 解析では局部集中の領域の応力を明示的にモデル化および計算するため、公称応力の調整を行う必要はほとんどありません。 ただし、計算済み FE 応力の線形的な調整が必要な場合、疲労解析ウィザードの一般的なスケール係数 Kt を使用できます。

se = Kt.s公称

se = 調整された弾性応力

耐久限度変更子

通常、SN 曲線データは標準サイズの研磨された試料のテストから取得します。この「ラボ」検査データを実際の工学的コンポーネントに適用すると、何らかの補正が必要になる場合があります。通常、この補正では、試料耐久限度に適用する「変更子」の形式を使用します。

変更子は、サイズ、サーフェス仕上げ、応力勾配、サーフェス処理、「荷重」タイプなどを考慮するために適用できます。これらの変更子は数多くの工学的文献に適切に文書化されているため、エンジニアは必要に応じて容易に入手することができます。

s末端変更 = s末端 .nサイズ . nサーフェス …

n は目的の変更子です

疲労解析ウィザードでは、サーフェス仕上げ効果および統計効果用の標準の変更子および計算済み組み合わせ値を入力するための一般的な変更子が供給されます。疲労解析ウィザードでは、上記の方法で試料耐久限度を調整して SN 曲線が変更され、1000 サイクル ポイントを中心として SN 曲線が回転します。

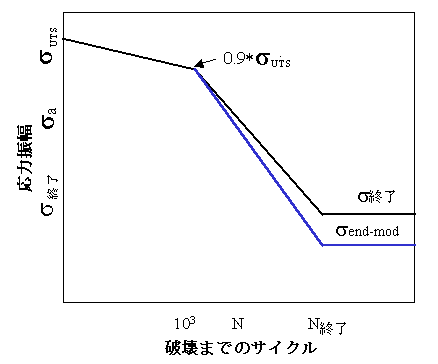
図 4

ひずみ寿命手法

ひずみ-寿命手法は、塑性変形が発生する材料の疲労破壊を予想する応力-寿命手法の改良として 1960 年代に開発されました。その原理は同じで、1 つのサイクル荷重について、ひずみ振幅(応力ではなく)が計測または計算され、ひずみ振幅対寿命の経験グラフと比較されます。応力-寿命のアプローチに比べ優れている点は、完全に弾性の変形に関するテスト データにおいて継承の想定がない点です。

ひずみ-寿命曲線

ひずみ-寿命曲線は、ラボで検査された試料の疲労動作を記述します。通常、試料は、完全反転のひずみが制御された荷重の条件で検査され、亀裂発生までの寿命に関連付けられます。ひずみ振幅の経験曲線対破壊までのサイクルがプロットされます。

変形が完全に弾性である低いレベルのひずみでは、疲労動作は応力振幅と互いに関連します。

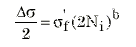
sf’ は、 疲労強度係数で、b は、疲労強度指数です。これら両方は、寿命に対する応力振幅の両対数フィットから抽出されます。

変形が完全にほぼ塑性である高いレベルのひずみでは、次のように、疲労動作はひずみ振幅と互いに関連します。

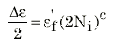
ef’ は、 疲労延性係数で、c は、疲労延性指数です。これら両方は、寿命に対するひずみ振幅の両対数フィットから抽出されます。

一般的なひずみ寿命曲線または Coffin-Manson 曲線は、次のように、これら 2 つの個別の直線曲線の組み合わせとして記述されます。

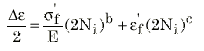
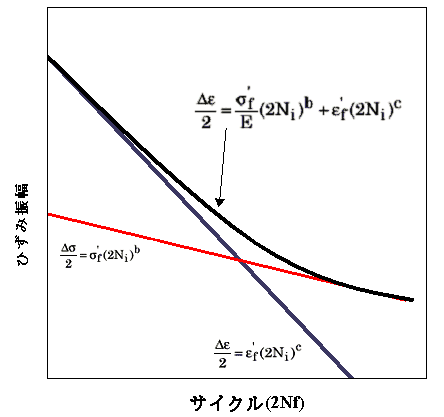
図 5 振幅一定ひずみ寿命曲線Coffin-Manson 関係。

使用できないさまざまなひずみ-寿命係数を近似化する

引張強度や係数など、より容易に使用できる単調データからひずみに基づく材料データを近似化するさまざまな方法があります。疲労解析ウィザードで使用される方法は、Seeger/Beste で使用される方法です。この方法は、ひずみに基づく疲労計算に関するさまざまな文献から入手できます。この手法では、次の式により、ひずみ寿命曲線(ひずみに基づく係数)が近似化されます。

鋼鉄:

その他:

平均応力補正

前述の新服一定寿命曲線は、完全反転の荷重、すなわちゼロの平均変位の条件において行われた材料テストを介して生成されます。実際の工学的な荷重サイクルでは、それは必然的に非ゼロの平均ひずみにおいて存在します。

ひずみサイクルにおける非ゼロの平均値の存在を補正するために、疲労解析ウィザードでは、簡潔な寿命曲線に対して、Morrow 補正および Smith-Watson-Topper 補正という 2 つの補正が使用されます。

Morrow 補正によるひずみ-寿命曲線

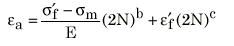
SWT 補正によるひずみ-寿命曲線

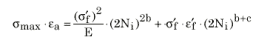
弾性-塑性材料データ

ひずみ-寿命データは、弾性限度を超えた周期荷重の対象となる材料から抽出されるため、周期応力-ひずみ材料曲線を定義する必要があります。

疲労解析ウィザードでは、周期的に安定した応力-ひずみ曲線の定義として、適切に文書化された 2 つの経験式が使用されます。

周期応力-ひずみ曲線は、材料定数 K' および n' を決定するために Ramberg-Osgood 関係を使用して構築されます。すなわち、周期硬化係数および周期硬化指数です。

Ramberg-Osgood 関係

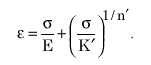
完全な周期応力-ひずみ曲線を生成するために、次の Masing の理論が使用されます。

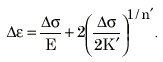
これら 2 つの関係を組み合わせて、2 つの材料定数から、周期的に安定した応力-ひずみ曲線の完全なヒステリシス ループを作成できます。

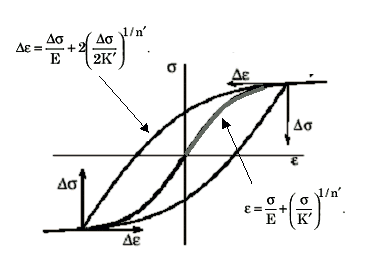
図 6 周期的に安定した応力-ひずみ曲線

Neuber 補正

多くの FE ベースの疲労コードでは、弾性 FE 解析の結果が使用されます。これによって、非線形解法を実行するための費用および時間を費やすことなく、比較的に簡潔な FE 計算を実行することができます。これらの弾性応力を使用してひずみに基づく寿命計算を後で実行する場合は、FE ベースの弾性応力を等価の弾性-塑性応力(およびひずみ)に変換する方法を設定します。

この変換に対して提案されている数多くの方法のうち、疲労解析ウィザードでは、その最も一般的な方法である Neuber 補正が使用されます。

応力-寿命アプローチ。

ひずみ-寿命アプローチ

このセクションの内容