損傷の理論的記述

概要:

損傷モデルは、複合材料などの弾性-脆性直交異方性材料の損傷の発生および進行的拡大をシミュレートします。このモデルは、主に繊維強化の複合材料をシュミレートする目的で使用します。損傷モデルでは、材料の応答の 3 つのフェーズを記述します。

1. 損傷のない材料応答。線形弾性である必要があります。
2. 損傷の開始
3. 進行的な損傷の拡大

モデルでは、材料の損傷は材料剛性の劣化として特徴付けられます。複合材料の繊維は、平行であり、要素の材料軸 1 方向にあると想定されます。4 つの異なる破壊モードが考慮されます。

• 引張における繊維破断
• 圧縮における繊維座屈およびよじれ
• 横方向の引張およびせん断におけるマトリックス割れ
• 横方向の圧縮およびせん断におけるマトリックス破砕

材料の動作は、σ = C_dε で定義されます。C_d は、損傷を反映し、次のように計算される弾性マトリックスです。

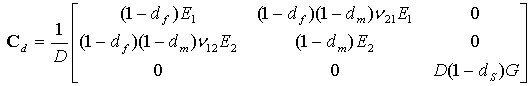
内容

• D=1-(1-d_f)(1-dm)ν₂₁ν₁₂ν
• d_f は、繊維損傷を表します。
• d_m は、マトリックス損傷を表します。
• d_s は、せん断損傷を表します。
• E₁ は、繊維方向のヤング率です。
• E₂ は、繊維に対して垂直方向の率です。
• G は、せん断係数です。
• ν₂₁ および ν₁₂ は、ポワソン比です。

損傷の開始:

損傷の開始の基準では、次の形式を持つ 4 つの異なる損傷モードが考慮されます。

モード I: 繊維の引張(>=0)
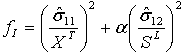
モード II: 繊維の圧縮(<0)
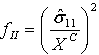
モード I: マトリックスの引張(>=0)
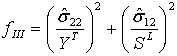
モード II: マトリックスの圧縮(<0)

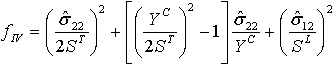
内容

• f_I、f_II、f_III、f_IV は、損傷の開始の基準に関連付けられた変数です。1.0 以上の値は、開始基準が満たされていることを示します。
• X^T は、縦方向の引張強度を表します。
• X^C は、縦方向の圧縮強度を表します。
• Y^T は、横方向の引張強度を表します。
• Y^C は、横方向の圧縮強度を表します。
• S^L は、縦方向のせん断強度を表します。
• S^T は、横方向のせん断強度を表します。
• α は、繊維の引張開始基準および 0<=α<=1 に対するせん断応力の影響を決定する係数を表します。

、 および は、=Mσ で計算される有効応力張力 のコンポーネントです。σ は公称応力で、M は、次のように定義される損傷演算子です。

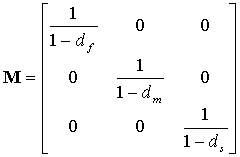
内部損傷変数 d_f、d_m および d_s は、4 つのモードに対応する損傷変数 d_ft、d_fc、d_mt および d_mc からの派生です。

d_f = …

• d_ft if 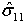>= 0
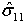• d_fc if < 0

d_m = …

• d_mt if 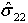>= 0
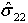• d_mc if < 0

d_s = 1-(1-d_ft)(1-d_fc)(1-d_mt)(1-d_mc)

損傷変数 d_ft、d_fc、d_mt、d_mc の方程式を次に示します。

損傷の進展:

上記セクションの損傷の開始に基づき、各モードに対して損傷変数の進展をここに定義します。材料軟化でのメッシュ依存を緩和するために、等価応力および変位を導入します。

同等の応力および変位は、4 つの損傷モードのそれぞれに対して定義します。

• 繊維引張モード:

  

  

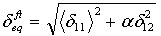
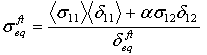
• 繊維圧縮モード:

  

  

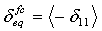
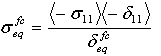
• 母材の引張モード:

  

  

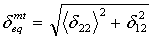
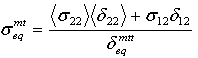
• マトリックス圧縮モード:

  

  

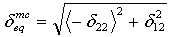
δ_ij = L_cε_ij および L_c では、特性長さは、積分点領域の平方根として計算されます。演算子 <x> は、<x> = (x+|x|)/2 として定義される Macauley 括弧演算子です。

同等の応力および変位に基づき、損傷変数は次のように計算されます。

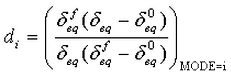
i は、4 つのモード I から IV (または d_ft、d_fc、d_mt および d_mc)に対応します。結果は、0 から 1 の範囲です。0 は、損傷がないこと、および要素で全荷重がサポートされることを示します。1 は、完全な損傷、および要素でその方向における荷重がサポートされないことを示します。

δ⁰_eq および σ⁰_eq は、開始条件が満たされた、初期同等変位および応力です。次のように定義されます。

。

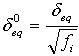
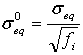δ^f_eq = 2G^c_i/σ⁰_eq は、この破壊モードにおいて材料に完全な損傷が発生している状態での同等変位です。G^c_i は、破壊モード i (引張または圧縮のいずれか)によって放散したエネルギーであり、損傷の進展を制御します。

損傷則のそれぞれにおける有限要素の最大サイズは、L_c <= 2 * E_iG^c_i / (X_i)² です。Eⁱ、G^c_i および Xⁱ は、順にヤング率、破壊エネルギー、強度です。i は、4 つの損傷モード I から IV に対応します(または、変数に基づいた指定に対応します)。

損傷安定化および粘性正則化

暗黙的解析における材料の軟化動作および剛性劣化によって引き起こされる収束の問題を解決するために、一般 Duvaut-Lions 粘性正則化スキームが導入されています。この正則化スキームでは、粘性損傷変数が次のように定義されています。

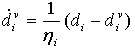
η_i は、粘性系の緩和時間を表す粘性係数です。d_i は、非粘性バックボーン モデルで評価される損傷変数で、この場合の i は損傷モード(I から IV、変数に対応した ft、fc、mt および mc)を意味します。正則化された損傷変数は、次のように更新されます。

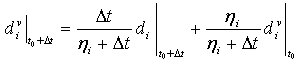
粘性材料の損傷応答は σ = C_d(dν)ε として定義されます。通常、小さな粘性パラメータを使用すると、結果を損なわずに、軟化スキーマにおけるモデルの収束率を向上させることができます。

その他: 関連する追加の計算を次に示します。

• 補足的な自由エネルギー密度:

  

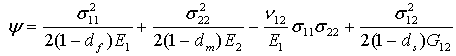
• 損傷エネルギー:

  

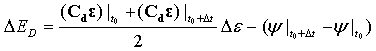
粘性エネルギー消散:

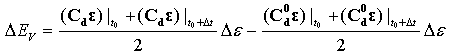
出典:

1. Hashin, Z. 著、「A fatigue failure criterion for fiber reinforced materials, Journal of Composite Materials」、7 (1973)、448-464。
2. Lapczyk, I. および Hurtado, J.A. 著、「Progressive damage modeling in fiber-reinforced materials, Composites: Part A」、38 (2007)、2333-2341。
3. Iannucci, L. および Ankersen, J. 著、「An energy based damage model for thin laminated composites, Composites Science and Technology」、66 (2006)、934-951。
4. Maimi, P.、Camanho, P.P.、Mayugo, J.A. および Davila, C.G. 著、「A continuum damage model for composite laminates: Part I - constitutive model, Mechanics of Materials」、39 (2007)、897-908。
5. Maimi, P.、Camanho, P.P.、Mayugo, J.A. および Davila, C.G. 著、「A continuum damage model for composite laminates: Part II - computational implementation and validation, Mechanics of Materials」、39 (2007)、909-919。