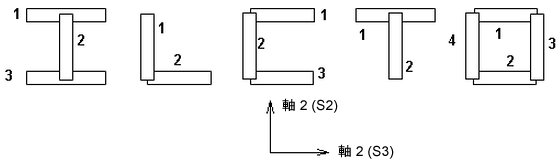
非線形ビーム要素では、[要素定義]で選択したオプションによって、3 種類の ASCII テキスト ファイルに結果を出力できます(「ビーム要素」>「高度なビーム要素パラメータ」の項を参照してください)。
力とモーメント
[力とモーメントの詳細出力]をアクティブにした場合、ビーム要素パーツの力とモーメントがサマリー ファイル(.AL)に書き出されます。このテキスト ファイルの形式は次のようになります。
Elem Node Force-1 Force-2 Force-3 Torque-1 Moment-2 Moment-3
ただし、
- Elem は要素番号を表します。各パーツは要素番号 1 から始まります。
- Node は局部要素節点を表します。節点 1 は I 節点、接点 2 は J 節点です。
- Force-1 は軸 1 方向の力を表します。
- Force-2 は軸 2 方向の力を表します。
- Force-3 は軸 3 方向の力を表します。
- Torque-1 は軸 1 のトルク(モーメント)を表します。
- Moment-2 は軸 2 のモーメントです。
- Moment-3 は軸 3 のモーメントです。
材料が非線形の挙動(塑性など)を受けず、中立軸の位置がわかっている場合、応力は指定されたジオメトリ、力、モーメント データから単純に計算できます。ただし、材料に降伏または非線形の挙動があった場合は、これらのデータから単純に応力を求めることはできません。このような場合は、応力(または、ひずみ)出力を使用します。
応力とひずみ
[詳細な応力出力]または[ひずみの詳細出力]のどちらかがアクティブな場合、ビーム要素パーツの応力とひずみはそれぞれ、ビーム応力出力(.BSO)ファイルとビームひずみ出力(.BST)ファイルに書き出されます。これらのテキスト ファイルの形式はどちらも同じで次のようになります。
Element Axial-Int Sec# Int2 Int3 State Stress-11 Stress-12 Stress-13
または
Element Axial-Int Sec# Int2 Int3 State Strain-11 Strain-12 Strain-13
ただし、
- Element は要素番号です
- Axial-Int は軸方向(1 軸)の積分点で、ユーザ指定の積分オーダによって 1 から順に番号が割り当てられます(最大 7 まで)。
- Sec# は断面番号です(断面が一連の長方形として扱われる場合)。
- Axial-Int は局部座標系の Y 方向(2 軸)の積分点で、ユーザ指定の積分オーダによって 1 から順に番号が割り当てられます(最大 7 まで)。
- Axial-Int は局部座標系の Z 方向(2 軸)の積分点で、ユーザ指定の積分オーダによって 1 から順に番号が割り当てられます(最大 7 まで)。
- State は、点が弾性であるか塑性であるかを示します
- Stress-11 は 11 方向の垂直応力です。
- Stress-12 は 12 方向の垂直応力です。
- Stress-13 は 13 方向の垂直応力です。
- Strain-11 は 11 方向の垂直ひずみです。
- Strain-12 は 12 方向の垂直ひずみです。
- Strain-13 は 13 方向の垂直ひずみです。
3 つの方向すべてにおける多くの積分点で構成されるビーム要素を想像してみてください(長さに沿った軸 1、断面の平面における軸 2 および 3)。応力出力はすべての積分点で得られるため、2x2x2 に積分オーダを設定した場合、各要素の応力が 8 行で出力されます。
要素内の積分点(Int1, Int2, Int3)の 3D 位置(X, Y, Z)を求めます。これは、形状に応じて次の計算で実施されます。
長方形
Y = C(Int2,INTy)*高さ*0.5 で、軸 2 方向の中立軸からの距離を計算します。
Z = C(Int3,INTz)*横*0.5 で、軸 3 方向の中立軸からの距離を計算します。
円
R = radius/2
R = R + C(Int2,INTy)*R
α = (2π/INTz)*(Int3-1)
Y = R*cosα で、軸 2 方向の中立軸からの距離を計算します。
Z = R*sinα で、軸 3 方向の中立軸からの距離を計算します。
中空円
R = (Ro+Ri)/2
R = R + C(Int2,INTy)*(Ro-Ri)/2
α = (2π/INTz)*(Int3-1)
Y = R*cos(α)で、軸 2 方向の中立軸からの距離を計算します。
Z = R*sin(α)で、軸 3 方向の中立軸からの距離を計算します。
ただし、
- X = C(Axial-Int,INTx)*0.5*縦+0.5*縦で、I 節点(= 節点 1)からの距離を計算します。
- INTx は X 方向の積分点の合計数です(局部座標系 1 軸の積分オーダ)。
- INTy は Y 方向の積分点の合計数です(局部座標系 2 軸の積分オーダ)。
- INTz は Z 方向の積分点の合計数です(局部座標系 3 軸の積分オーダ)。
量 C (i, 積分オーダ)は、次の表に基づきます。
| 積分オーダ | C(i, Integration Order) | ||||||
|---|---|---|---|---|---|---|---|
| i = 1 | i = 2 | i = 3 | i = 4 | i = 5 | i = 6 | i = 7 | |
| 1 | 0 | - | - | - | - | - | - |
| 2 | -1 | 1 | - | - | - | - | - |
| 3 | -1 | 0 | 1 | - | - | - | - |
| 4 | -1 | -0.333 | 0.333 | 1 | - | - | - |
| 5 | -1 | -0.5 | 0 | 0.5 | 1 | - | - |
| 6 | -1 | -0.6 | -0.2 | 0.2 | 0.6 | 1 | - |
| 7 | -1 | -0.666 | -0.333 | 0 | 0.333 | 0.666 | 1 |
一般断面
各セクションはそれぞれ別個の 4 角形として扱われます。C(i,j)は、位置の特定に直接適用されます。
予設定断面
各セクションは以下のようにそれぞれ別個の 4 角形のように扱われ、セクション番号を伴います。