ビーム要素は、3D(3 次元)の X、Y、Z 空間で任意の方向に使用可能な 2 節点のメンバです。 要素の方向を定義するには、追加の節点(K 節点)が必要です。ビームは、モーメント、トルク、および力を伝達するものであり、汎用の 6 自由度(DOF)要素(メンバの各端に 3 つのグローバルな並進および回転コンポーネント)です。
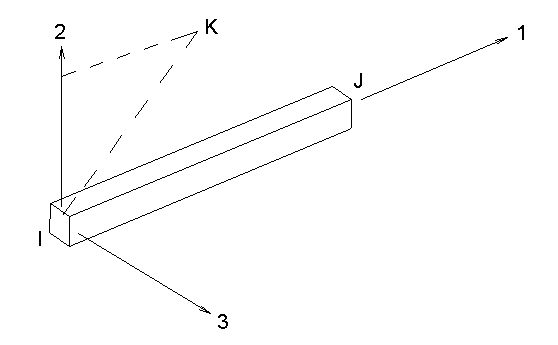
図 1: ビーム要素における K 節点の定義
3D ビーム要素は、3 次元の均一断面要素であり、一般的なビーム/フレーム問題における大きな変形と弾塑性解析の実行が可能です。MES/非線形構造解析では、シェイプの断面変化は考慮されません。
外部的には、ビームには 6 つの自由度(3 つの変位と 3 つの回転)があります。解析の出力には、ビームの材端力、軸応力、関連するせん断応力などが含まれます。完全 3D の並進および回転運動がサポートされます。 3D ビーム要素は、大きな変形や材料の非線形効果をともなう曲げ、ねじり、引張りの動作が生じる場合の解析で頻繁に使用されます。
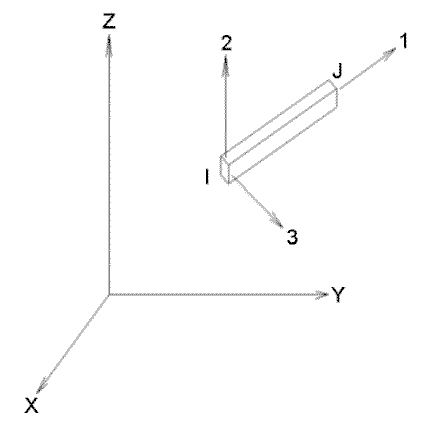
図 2: 3D ビーム要素の例
ビーム要素におけるパーツ、レイヤ、サーフェスのプロパティ
次の図は、ビームのパーツ、レイヤ、サーフェスのプロパティによってコントロールされる内容を示しています。
| 部品番号 | 要素データ(材料モデル、詳細出力など)、応力なしの参照温度、材料特性 |
| レイヤ番号 | 断面プロパティ([全般]セクション タイプ以外) |
| サーフェス番号 | 方向 |
ビーム要素の方向
ほとんどのビームには、曲げの強軸と曲げの弱軸があります。ビーム メンバはラインで表され、ラインは断面の固有方向がないオブジェクトであるため、3 次元空間で強軸または弱軸の方向を指定する手段が必要になります。この方向は、線のサーフェス番号によってコントロールされます。
さらに具体的に言うと、線のサーフェス番号により、K 節点と呼ばれる点が空間に作成されます。ビーム要素の 2 つの材料端(I 節点、J 節点) および K 節点により平面が形成されます(図 3 を参照)。 ビーム要素は、ローカル軸 1、2、3 によって定義されます。軸 1 は I 節点から J 節点の方向で、軸 2 は I 節点、J 節点、および K 節点で形成される平面にあり、軸 3 は右手の法則によって形成されます。要素の各軸を設定することにより、断面のプロパティ A、Sa2、Sa3、J1、I2、I3、Z2、Z3 を[要素定義(Element Definition)]ダイアログに適切に入力できます。
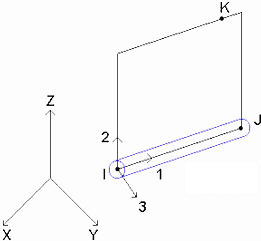
図 3: 軸 2 は I 節点、J 節点、および K 節点の平面にあります。
たとえば、それぞれに W10x45 I-beam を含む 2 つのモデルの一部を図 4に示します。両方のメンバの物理的方向は同じである点に注意してください。ウェブは平行です。ただし、モデル A のビーム要素上、およびモデル B のビーム要素の横に K 節点を配置するように選択されています。断面プロパティが同じであっても、軸 2(I2)の回りの慣性モーメントと、軸 3(I3)の回りの慣性モーメントは別々に入力する必要があります。
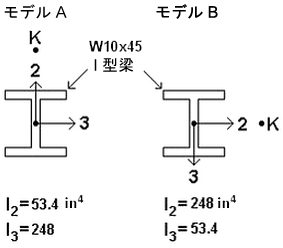
図 4: ビーム要素に適した断面プロパティを入力
既定の K 節点の場所(ラインの表面番号によるビーム方向に対して)
表 1 は、さまざまなサーフェス メンバに対して K 節点がどこに配置されるかを示しています。場所の第 1 候補は、I 節点、J 節点、および K 節点が平面を形成する場合に K 節点が作成される場所です。 ビーム要素が K 節点と同一直線上にある場合、固有の平面は形成されません。この場合、場所の第 2 候補は、その要素に使用されている場所です。
| 表 1: 表面番号と K 節点の相関関係(軸 2 方向) | ||
|---|---|---|
| サーフェス番号 | K 節点の場所の第 1 候補 | K 節点の場所の第 2 候補 |
| 1 | +Y の 1E14 | -X の 1E14 |
| 2 | +Z の 1E14 | +Y の 1E14 |
| 3 | +X の 1E14 | +Z の 1E14 |
| 4 | -Y の 1E14 | +X の 1E14 |
| 5 | -Z の 1E14 | -Y の 1E14 |
| 6 | -X の 1E14 | 1E14 in -Z |
K 節点の座標が原点から極端に離れた距離にあることに注目してください。この配置には非常にもっともな理由があります。任意の現実世界の解析モデルの限定された寸法を考慮してください。幅、長さ、および高さは、K 節点の場所までの距離と比較して重要ではありません。たとえば、+Z 軸が上方向であり、50 メートル幅の構造の床用根太に表面 2 を使用する場合、Z 軸から +/- 25m (または 50m)変位することによる梁の垂直軸のずれは 極微量です。長さの単位がミリメートルであると仮定します。(50,000mm / 1E14mm)の逆正弦は 0.0000000143°です(すべての実用上の目的においてゼロ)です。このため、非常に幅広い構造上の複数の点に配置されている場合でも、垂直方向の梁に対して複数の K 節点を定義する必要がありません。
表面番号を変更できます。したがって、梁の既定の方向も変更できます。適当なビーム要素を選択([選択]
[選択][ライン]コマンドを使用)し、表示領域を右クリックします。[属性変更]コマンドを選択し、[表面]フィールドの値を変更します。
ユーザ定義のビーム要素の方向
場合によっては、全体 K 節点の場所が適切でないことがあります。その場合、[選択] > [選択] > [ライン]コマンドを使用して[FEA エディタ(FEA Editor)]環境でビーム要素を選択し、表示領域で右クリックしてください。[ビーム方向] > [新規]コマンドを選択してください。これらのビームの K 節点の X、Y、Z 座標を入力してください。モデルの特定の節点を選択するには、頂点をクリックするか、頂点の ID を[ID]フィールドに入力してください。指定された座標に青色の円が表示されます。図 5 は、原点を k 節点として定義する場合のビーム方向の例を示しています。
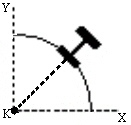
図 5: 傾きのあるビーム方向
軸 1 の方向を反転する方法
軸 1 の方向は、FEA エディタで反転することができます。変更する要素を選択 ([選択] > [ラインを選択])し、右クリックから[ビーム方向] > [I および J 節点を反転]を選択してください。これは、荷重が I 節点および J 節点に依存する場合や、軸 3 の方向をコントロールする場合に便利です(軸 3 は軸 1 および 2 の右手の法則から形成されているため)。 選択された要素のいずれかが、I/J の方向に依存する荷重を持つ場合、荷重を反転するかどうかが尋ねられます。I 節点および J 節点は交換されているため、[Yes]を選択して荷重の入力を反転することにより、現在のグラフィカル表示が維持されます。I 節点および J 節点は反転され、荷重を受ける I/J 端も反転されます。[No]を選択した場合は元の入力が維持されます。すると、I 節点の位置が変更されているため、I 節点の開放端が要素の逆の端に切り替わります。
正しい軸の方向を確認する方法
[表示] [表示設定] [オブジェクト表示設定] [要素軸]コマンドを使用すると、要素の方向を FEA エディタ環境に表示することができます。また、[結果オプション] [表示] [要素方向]コマンドを使用して、結果環境で要素の方向を確認することもできます。[軸 1]、[軸 2]および/または[軸 3]を順に赤、緑、青の矢印で表示するように選択します。図 6 を参照してください。
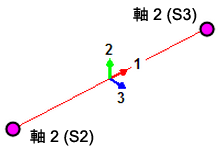
図 6: ビーム方向の記号
それぞれの軸に異なる矢印が使用されています。
ビーム要素の断面特性を指定する
[要素定義]ダイアログ ボックスには、ビーム要素の特性を定義するときに使用できる 2 つのオプションがあります。一般的な断面を使用する場合や、あらかじめインストールされているビーム断面ライブラリのいずれかで見つけることができる断面を使用する場合は、[事前に定義された]オプション([断面タイプ]ドロップダウン ボックス)を選択し、[断面ライブラリ]ダイアログ ボックスで特性を定義してください。これは、パーツ内のそれぞれのレイヤに対して実行してください。[断面の特性]スプレッドシートのレイヤ行をハイライトし、[断面ライブラリ]ボタンをクリックしてください。
- 非線形のビームでは、実際のシェイプと断面の寸法が必要とされるため、断面プロパティ(A、J1、I2 など)を スプレッドシートに直接入力することはできません。断面ライブラリを使用してシェイプを入力する必要があります。同様に、断面の特性(A、J1、I2 など)は参照用にのみ表示されます。解析では、必要なプロパティが、シェイプの寸法に基づいて計算されます。
- ビームの長さに沿って連続した断面を生成してテーパービームを近似するには「可変断面作成ウィザード」のページを参照してください。
一般的な梁の特性を定義する
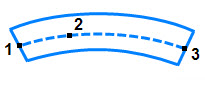
特殊な断面を使用する場合は、[一般]オプション([断面タイプ]ドロップダウン ボックス)を選択してください。[一般]テーブルは、複数のインデックスを指定することにより、ビーム要素の断面を定義する場合に使用されます。 それぞれのインデックスは、断面のストリップです。インデックスには、厚さを持つ 4 辺形または円弧を使用できます。 4 辺形のインデックスは、2 つの点によって定義されます。 これらの点は、図 7(a) に示すように、4 辺形の端部の中間点です。 円弧のインデックスは、図 7(b) に示すように、3 つの点によって定義されます。. 点 1 と点 3 は、円弧の終端で、点 2 はアーク上のもう 1 つの点です。
|
(a) 4 辺形断面 |
(b) 円弧断面 |
| 図 7: ストリップの例 | |
ストリップごとに、各点の YY 座標と ZZ 座標およびその点におけるセグメントの幅を定義してください。YY 座標は、ビームのローカル軸 2 を参照し、ZZ 座標は、ローカル軸 3 を参照します。両方の寸法は、断面の重心の計算結果から測定されます。最終的なシェイプの重心は、ビーム要素の軸上にあります。 YY 座標と ZZ 座標は、ストリップの中間点に対応する必要があります。
データが入力されると、[要素定義]ダイアログの[プレビュー]ウィンドウにストリップが表示されます。[プレビュー]ウィンドウには次のような機能があります。
- カーソルのある行に対応するストリップがハイライトされます。 スプレッドシートの別の行にカーソルを移動すると、各ストリップが表示されます。
- マウスのホイールを回転すると、[プレビュー]ウィンドウがズーム インまたはズーム アウトされます。
- マウスの左ボタンを押したままドラッグすると、[プレビュー]ウィンドウがパンニングされます。
- 右クリックから[全体表示]を選択すると、スケッチ全体が表示されます。
断面が開いている(I ビーム、導管など) か、または閉じている(パイプ、チューブなど)かによって、ねじり定数(J1)の計算に影響されます。 これらの基準により、ねじり定数の計算方法が次のように決定されます。
- 閉じた断面:
- それぞれのインデックスの断面番号は同じになります(ゼロ以外)。
- 前のストリップの最後の点の座標が、次のストリップの最初の座標と一致します。
- 断面の最後のストリップ上の最後の点の座標が、断面の最初のストリップの最初の座標と一致します。このようにして、ストリップは連続的に断面内に存在します。
- 開いた断面:
- それぞれのインデックスの断面番号は同じになります(ゼロ以外)。
- ストリップは、閉じた順序で相互に連結されることはありません。
- その他の断面:
- 断面番号が 0 の場合、ねじり定数は、極慣性モーメント(Iyy+Izz)を使用して計算されます。これは、丸いチューブにのみ該当します。
同様に、一般的な断面は、複数の部分断面で構成することができます。その場合、各部分断面内のすべてのインデックス(スプレッドシートの各行)は、[断面]列に同じ番号を持つ必要があります。部分断面の間でストリップが共有されている場合は、共有されているインデックスの断面番号を[共通]列に指定する必要があります。 たとえば、断面が 2 つの部分断面 Section 1 と Section 2 で構成されているとします。Section 1 のインデックス 2 は、Section 2 のインデックス 5 と同じです。インデックス 2 の[共通]列には、2 を入力する必要があります。 インデックス 5 の[共通]列には、1 を入力する必要があります。 一連のインデックスによって閉じた断面が定義される場合、これらのインデックスは固有の断面内に配置される必要があります。
一般断面タイプの例
図 8(a) に示されている中空長方形の断面は、4 つの長方形断面を使用して描画されます。ソフトウェアで断面を閉じた断面として扱うには、それぞれの点が厳密に 2 つのインデックスで使用されていることが必要です。そのため、図 8(b) に示された 4 つの 4 角形が使用される必要があります。実際には、断面のジオメトリが真の断面と完全に一致することはありません。ただし、この差異による解析上の影響はわずかです。図 8(c) に示されるような 4 つの 4 角形を定義する場合には、開いた断面を定義することになります。開いた断面に基づいて計算されたねじり定数を閉じた断面に使用する場合の影響は、他の断面の値における小さな相違点よりはるかに重大です。断面は、図 2 に示すように、一般断面タイプを使用して定義する必要があります。
|
理論上の結果: A = 64.0 in2 Iyy = 1301.3 in4 Izz = 1061.33 in4 J1 = 1561.3 in4
(a) 実際のジオメトリ |
計算結果: A = 64.0 in2 Iyy = 1281.3 in4 Izz = 1050.3 in4 J1 = 1561.3 in4
(b) 断面を定義するための正しい手法 この入力を表 2 に示します。 |
|
計算結果: A = 64.0 in2 Iyy = 1301.3 in4 Izz = 1061.3 in4 J1 = 62.2 in4
(c) 断面を定義するための間違った手法 ストリップ間の点は一致しないため、ねじり定数の計算に間違いが生じます。 |
|
| 図 8: 中空 4 角形断面 | |
表 2: 図 8(b) の断面の定義
| インデックス | 断面 | 幅 (1) | YY(1) | ZZ(1) | 幅 (2) | YY(2) | ZZ(2) | 共通 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | -5.5 | -5 | 1 | -5.5 | +5 | 0 |
| 2 | 1 | 2 | -5.5 | +5 | 2 | +5.5 | +5 | 0 |
| 3 | 1 | 1 | +5.5 | +5 | 1 | +5.5 | -5 | 0 |
| 4 | 1 | 2 | +5.5 | -5 | 2 | -5.5 | -5 | 0 |
その他の 4 つの断面ジオメトリ タイプを図 9 に示します。 すべての図において、線は厚さを表します。
|
|
|
|
| (a) | (b) | (c) | (d) |
| 図 9: その他の断面のジオメトリ タイプ | |||
断面 (a) では、それぞれの 4 角形に対して 1 つずつ、3 つの断面が必要です。左側の 4 角形は、5 つのインデックスを使用して作成する必要があります。右の頂点は、2 つのインデックスに分割し、他の 2 つの断面と共通に定義できるようにする必要があります。共通のインデックスは両方の断面に定義する必要があるため、この断面には合計 13 個のインデックスが必要になります。断面 (b) には、2 つの断面が必要です。それぞれの 4 角形は、両方の断面に共通として定義されたセンター ピースを使用して定義される必要があります。 この断面には、8 個のインデックスが必要です。断面 (c) には、3 つの断面が必要です。2 つの 4 角形のチューブ断面は閉じた断面であるため、これらは別々に定義される必要があります。これらの断面の間で共通として定義されるインデックスはありません。この断面には、9 個のインデックスが必要です(水平のピースに連結される 2 つの 4 角形の側面が分割される必要はありません)。断面 (d) に必要な断面は 1 つのみです。この断面には、3 つのインデックスが必要です。
一般断面データのインポート
[インポート]ボタンを使用して、断面データを csv ファイルからインポートすることができます。 csv ファイルには、11 列のデータが含まれる必要があります。これらの列の値は、左から右に、「断面の座標と寸法」の表の[断面]列から順に一致する必要があります。[インデックス]列に対応する列は含めないでください。
断面ライブラリ
断面ライブラリを使用するには、[断面タイプ]ドロップダウン ボックスで[事前に定義された]オプションを選択する必要があります。特性を定義するレイヤを[断面の特性]スプレッドシートで選択し、[断面ライブラリ]ボタンを押します。
断面ライブラリの使用
断面ライブラリを使用するには、まず最初に断面プロパティを定義するレイヤを選択します。レイヤを選択したら、[断面ライブラリ]ボタンをクリックします。
既存のライブラリから断面を選択する方法
- [断面データベース:]ドロップダウン メニューでライブラリを選択します。ソフトウェアではビーム断面ライブラリの複数のバージョンが提供されています(注: ライブラリはソフトウェアで I 2 に対応する I YY (AISC マニュアルで定義されています)を使用して設定されています)。
- 断面のタイプを、[断面タイプ]プルダウン メニューを使用して選択します。各 AISC データベースで使用可能なタイプ記号は、「ビーム断面ライブラリ」ページの表 5 に示されています。さらに、非 AISC ライブラリからの形状記号と対応する AISC断面タイプを相互に関連付けるために、同じページの表 2 の情報を使用できます。AISC ライブラリには、一部の 非 AISC ライブラリで使用できるすべての断面タイプが含まれていないため、この表は包括的ではありません。
- [断面名称]リストで断面の名前を選択します。リストの上のフィールドに文字列を入力することにより、名前の検索ができます。
- ダイアログ ボックスの[断面特性]セクションで値を確認します。問題ない場合は、[OK]をクリックします。
新しいライブラリの作成と断面のライブラリへの追加
あらかじめインストールされているライブラリを変更することはできません。ただし、カスタム ライブラリを作成し、それらにユーザ定義の断面を追加することができます。また、あるコンピュータで作成したライブラリを新しいコンピュータにコピーし、プログラムに追加することもできます。カスタム ライブラリと断面の作成手順については、「カスタム断面ライブラリと形状エントリの作成」ページで説明されています。
共通形状を定義する方法
ユーザが寸法を定義できる、一般的な断面のリストを含むプルダウン メニューが[断面ライブラリ]ダイアログ ボックスの右上隅にあります。次の形状が含まれます。
- 円形
- 直角座標
- 中空の矩形
- 広いフランジの梁
- C 形チャネル
- L-タイプ(角度)
これらすべての形状で、適切な寸法を入力します。形状を選択すると、スケッチとデータ入力フィールドが表示されます。
共通形状を選択して寸法記入するには
- ビーム部品の[要素定義]ダイアログ ボックスに移動します。
- [断面タイプ]が[事前に定義された]に設定されていることを確認します。
- [断面の特性]の表でレイヤ(行)を選択し、[断面ライブラリ]ボタンをクリックします。
- [断面データベース]プルダウン メニューから[ユーザ定義]オプションを選択します。
- ダイアログ ボックスの右上コーナーのプルダウン メニューから目的の共通形状を選択します。
- ダイアログ ボックスの右側に、適切な寸法を入力します。断面特性が計算されて表示されます。
- [OK]をクリックします。
- 次のレイヤに対して手順 3 ～ 7 を繰り返し、[OK]をクリックして[要素定義]ダイアログ ボックスを終了します。
その他のビーム要素パラメータ
ビーム要素を使用する場合、このパーツの材料モデルを[材料モデル]ドロップダウン ボックスに指定する必要があります。
- 材料が応力/ひずみ曲線の弾性領域にとどまる場合は、[等方性]オプションを選択してください。
- 材料が塑性変形を受ける場合には、次のいずれかを選択してください。
- [等方硬化をともなうフォンミーゼス]。 このモデルでは、双線形曲線を使用して応力/ひずみ関係をコントロールします。
- [等方硬化をともなうフォンミーゼス 曲線]。 この場合、降伏応力を超えた複数の点の応力/ひずみ曲線を使用して、応力/ひずみ関係をコントロールします。
- 材料に温度に基づいた異なる特性があるが、応力/ひずみ曲線の弾性領域にとどまる場合は、[温度依存等方性]オプションを選択します。材料に温度に基づいた異なる特性があるが、可塑変形が発生する場合は、[温度依存の塑性]オプションを選択します。
材料モデルが[等方硬化をともなうフォンミーゼス]に設定されている場合、[応力更新手法]が使用されます。 これにより、材料が可塑性に移行するときの構造方程式(応力/ひずみ則)を積分するための数値アルゴリズムがコントロールされます。 [応力更新方法]で使用可能なオプションは次のとおりです。
- [陽解法]: (独自手法)。このオプションでは、構成方程式の積分に陽的サブ増分前進オイラー法を使用します。[明示的]オプションは、実行速度が速いため、単純な問題(単純な引張りなど)に最適です。ただし、この手法は、荷重や時間ステップ サイズに大きく影響されます。非線形の反復解法で推奨される選択([設定] [モデル設定] [パラメータ] [高度] [平衡]タブで設定)は、線探索による結合 Newton 法です。ただし、モデル内の他の機能によって異なり、場合によっては異なる設定が必要になることもあります。
- [一般化された中点法]: このオプションでは、構成方程式の積分に陰解法を使用します。この場合、誤差の蓄積が減少し、応力更新プロセスが無条件に安定であることが保証されます。そのため、このオプションは、複雑な解析(厳しい可塑性など)により適しています。 非線形の反復解法で推奨される選択([設定] [モデル設定] [パラメータ] [高度] [平衡]タブで設定)は、ラインサーチを用いる完全ニュートン法です。ただし、モデル内の他の機能によって異なり、場合によっては異なる設定が必要になることもあります。
[応力更新方法]が[一般化された中点法]に設定されている場合は、[一般化中間点のためのパラメータ]入力が使用されます。 0 以上 1 以下の範囲で入力することができます。パラメータを 0 (ゼロ)に設定した場合、完全陽解法のいずれかのアルゴリズムが得られます([応力更新方法]で[陽解法]オプションに設定した場合と同じ)。ただし、解法は無条件に安定ではありません。パラメータを 0.5 以上に設定した場合、解法は無条件に安定します。パラメータを 0.5 に設定した場合の解法は中間点アルゴリズムとして知られています。1 に設定した場合の解法は完全後退オイラー法または最接近点アルゴリズムとして知られており、完全陰解法です。値 1 は、他の値よりも精度が向上します。特に、大きな時間ステップの場合に向いています。
[解析タイプ]ドロップダウンを使用して、推測される変位のタイプを設定してください。 [微小変形]は、運動がなく、小さなひずみしか受けないパーツに適しています。この場合、大きな変形の結果生じた非線形の幾何学的影響は無視されます (これにより、[高度]タブの[解析の定式化]が[非線形材料に限る]に設定されます) 。[大変形]は、運動や大きなひずみを受けるパーツに適しています ([高度]タブの[解析の定式化]も解析の必要性に応じて設定される必要があります)。
[オプション][解析]タブにある[非線形解析のための既定として大変形を使用]オプションを使用して、[解析タイプ]の既定値を小変形にするか大変形にするかを設定します。 [温度依存等方性]または[温度依存の塑性]の材料モデルを使用している場合、[熱]タブの[無応力時の参照温度]フィールドに値を指定する必要があります。熱応力は、節点温度とこの値との間の差から生成されます。
高度なビーム要素パラメータ
ビーム要素に使用する定式化手法を[解析定式化]ドロップダウン ボックス([高度]タブ)で設定してください。
- [非線形材料に限る]オプションが選択されている場合、非線形材料モデルの効果が考慮されますが、すべての計算は、変形のないジオメトリに基づいて実行されます。 したがって、この定式化は、小さなひずみを受け、運動がないパーツに適しています。これは、[一般]タブの[解析タイプ]が[微小変形]に設定されている場合、使用可能な唯一のオプションです。
- [Total Lagrange 法]オプションを選択すると、すべての静的変数および運動学変数について、初期状態で変形されていないモデルの構成が参照されます。この定式化は、運動と小さなひずみを受けるパーツに適しています。材料特性は、エンジニアリングにおける応力およびひずみである点に注意が必要です。
- [Updated Lagrangian 法]では、すべての静的変数および運動学的変数に対して、モデルの最後に計算された形状が参照されます。 この定式化は、運動と大きななひずみを受けるパーツに適しています。材料特性は、実際の応力およびひずみである点に注意が必要です。
次に、各ビーム要素軸の積分オーダを、[第 1 オーダ積分]、[第 2 オーダ積分]、および[第 3 オーダ積分]ドロップダウン ボックスで選択してください。[第 1 オーダ積分]ドロップダウン ボックスのオプションは、主軸(要素の長さ方向の軸 1)におけるガウス求積法に使用されます。[第 2 オーダ積分ドロップダウン ボックスのオプションは、副軸(軸 2)におけるガウス求積法に使用されます。 [第 3 オーダ積分]ドロップダウン ボックスのオプションは、第 3 軸(軸 3)におけるガウス求積法に使用されます。 高次の積分オーダを使用すると精度が向上しますが、解析時間は長くなります。
[大きな剛体回転]: 解析中どこかで部品の要素のいずれかが大きな剛体回転を受ける場合、[大きな剛体回転]オプションをアクティブ化してください。アクティブ化すると、回転マトリックスは、それぞれの反復時に保存されますが、応力結果の精度が向上します。このオプションがアクティブ化されていない場合、パーツが剛体回転を受けると、応力が一定にならずに増加し、ある程度の不正確さが生じます。パーツ内のビーム要素が大きな変形を受ける場合、回転には無関係に、このオプションをアクティブ化する必要はありません(ただし、下記のヒントを参照してください)。
非線形の大きなわたみや大きな運動の解析の場合と同様、解析のステップ数が増加するほど、結果の精度が向上します。場合によっては、ビーム パーツの 90 度の回転あたり 100 回の計算ステップや、回転 1 度あたり約 1 回の計算ステップに設定することが必要になることもあります。
追加出力: ビーム要素に関する結果出力として 4 種類を作成できます。 追加出力をテキスト フォーマットにする(Notepad、Word、その他の任意のテキスト エディタで読む)か、またはバイナリ フォーマットにする([結果]環境によって読み出す)かについては次に示します。テキスト出力ファイルのフォーマットについては、(「ビーム要素のテキスト結果出力」)のページで説明されています。
- [力とモーメントの詳細出力]の場合、各時間ステップにおける各ビーム要素力とモーメントが出力されます。 これらの結果は、サマリ ファイル(.AL というテキスト フォーマット)に書き出されます。
- [力とモーメントの詳細出力]の場合、時間ステップごとの各積分点における各要素の応力値が出力されます。これらの結果は、ビームの応力出力ファイル(.BSO というテキスト フォーマット)に書き出されます。
- [ひずみの詳細出力]の場合、時間ステップごとの各積分点における各要素の応力値が出力されます。これらの結果は、ビームのひずみ出力ファイル(.BST というテキスト フォーマット)に書き出されます。
- [応力とひずみのバイナリ出力]の場合、時間ステップごとの各積分点における各要素の応力値とひずみ値が出力されます。これらの結果はバイナリ フォーマットであるため、[結果]環境でしか表示できません。 このオプションがアクティブ化されていない場合、これらの結果を[結果]環境で利用することはできません。 注: [結果コンター] > [ひずみ] > [ビームとトラス]メニューを使用して[結果]環境に表示されたビームの応力は、計算された力とモーメントをそれぞれ、ビームの断面積と断面係数で割った結果に基づいています。そのため、これらの結果では降伏は考慮されていません。[応力の詳細出力]または[応力とひずみのバイナリ出力]オプションをアクティブ化することにより、計算された応力が出力され、すべての非線形効果が考慮されます。このオプションがアクティブ化されている場合は、[結果の照会] [照会] [ビーム応力の詳細]または[結果の照会] [照会] [ビームひずみの詳細] メニューを使用することにより、[結果]環境に正しい応力とひずみを表示することができます。
ビーム要素の利用に関する基本ステップ
- 単位系が定義されていることを確認してください。
- モデルで使用される解析タイプが非線形になっていることを確認します。
- ビーム要素に指定するパーツの[要素タイプ]見出しを右クリックしてください。
- [ビーム]コマンドを選択してください。
- [要素定義]の見出しを右クリックします。
- [要素定義を編集]コマンドを選択してください。
- [一般]タブで、このパーツに該当する材料モデルを[材料モデル]ドロップダウン ボックスで選択し、断面の形状を[断面タイプ]ドロップダウン ボックスで選択してください。
- [事前に定義された]オプション([断面タイプ]ドロップダウン ボックス)を選択した場合、[レイヤ]を選択して[断面の特性]スプレッドシートに定義し、[断面ライブラリ]ボタンを押してください。断面を選択または入力してください。
- または、[一般]オプションを選択した場合、表示されるテーブルに断面を定義してください
(上記のトピック「ビーム要素の断面特性を指定する」を参照)。
- [OK]ボタンを押します。