유한 요소 형식화는 천이 열 전도 방정식에서 사용되는 열 소스 항을 풀 때 사용됩니다.
전자기 현상을 설명하는 방정식은 전자기 필드 모델링에서 찾을 수 있습니다. 유한 요소 형식화는 해당 페이지의 방정식 (19)를 풀 때 사용됩니다.
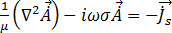 (19)
(19)
열 소스 항을 얻기 위한 방정식 (21)
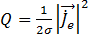 (21)
(21)
방정식 (22)를 풀기 위해 기존 냉각 솔버에서 사용:
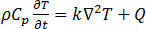 (22)
(22)
방정식 (19)는 시간 고조파 간략식이므로 자기 벡터 포텐셜 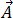 및 와전류
및 와전류 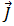 가 복잡한 숫자로 표현될 수밖에 없습니다.
가 복잡한 숫자로 표현될 수밖에 없습니다.
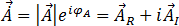 (23)
(23)
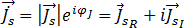 (24)
(24)
여기서 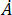 및
및 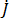 은 풀고 있는 항의 카테시안 성분을 의미하고,
은 풀고 있는 항의 카테시안 성분을 의미하고, 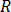 및
및 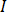 은 복잡한 숫자의 실제 및 가상 성분에 대한 아래 첨자입니다.
은 복잡한 숫자의 실제 및 가상 성분에 대한 아래 첨자입니다.
벡터의 각 x, y, z 성분에 대해 개별적으로 갤러르킨 근사가 방정식 (19)에 적용되었습니다.
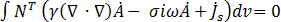 (25)
(25)
그 결과 다음 형식의 세 방정식이 나옵니다.
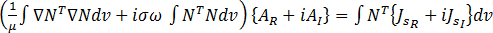 (26)
(26)
여기서 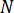 은 형상 함수를,
은 형상 함수를, 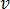 은 요소의 체적을 의미합니다. 방정식 26은 자기 벡터 포텐셜
은 요소의 체적을 의미합니다. 방정식 26은 자기 벡터 포텐셜 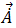 의 알 수 없는 카테시안 성분의 실제 및 가상 성분 모두에 대한 각 4면체 요소에서 해결됩니다. 따라서
의 알 수 없는 카테시안 성분의 실제 및 가상 성분 모두에 대한 각 4면체 요소에서 해결됩니다. 따라서 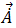 에는 해결해야 할 자유도 6도가 있습니다.
에는 해결해야 할 자유도 6도가 있습니다.