실제로 대부분의 구조는 제한된 범위의 하중 강도에 대해서만 선형 또는 선형에 가까운 반응을 보입니다. 하중이 높을수록 구조의 강성이 현저하게 변경되어 비선형 반응을 보일 수 있습니다.
비선형에 대한 간단하지만 사실적인 그림에서는 상단(하단은 고정되고 상단은 자유로움)에서 수평력 H 및 하향 수직력 V가 적용된 L 길이의 얇은 기둥을 고려합니다. 끝의 작은 아래쪽 이동을 무시하는 이러한 하중 시스템의 1차 효과는 u라는 크기만큼 가로로 기둥의 상단을 변형하는 것입니다. 이제 이 변위된 구성에서 구조 및 하중을 고려하면 기둥 베이스의 벤딩 모멘트 M이 다음과 같다는 것을 바로 확인할 수 있습니다.
M = HL+Vu
M이 단순히 외부 하중에 대한 함수가 아니라 u에 따라서도 달라진다는 사실은 문제가 비선형이라는 것을 바로 보여줍니다. 분명히 구부러진 기둥에서 작용하는 수직 하중의 효과는 횡변위를 더 늘리는 것이므로 문제를 직접 해결할 수 없습니다. 그러나 적용된 하중 H 및 V를 작은 증분으로 분할하고 하중을 필요한 레벨까지 점진적으로 형성하여 실제 솔루션에 가까이 접근할 수 있습니다.
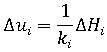
- i는 증분 번호입니다.
- ki는 기둥 끝의 현재 횡강성입니다.
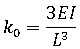
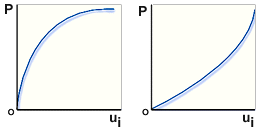
비선형 반응에 대한 하중-변위 플롯
.왼쪽 연화 반응, 오른쪽 경화 반응, P 비선형 하중, ui 변위 플롯
위의 예제에서는 비선형 하중 변형 경로를 따르는 근사 방법을 사용했습니다. 이 방법에서는 매우 작은 단계만 수행해도 실제 또는 정확한 반응을 찾을 수 있습니다. 비선형 반응에 대한 보다 정확한 모델의 기반을 이해하려면 구조가 실제 하중 변형 경로의 각 점에서 평형 상태여야 함을 인식해야 합니다. 실제로 하중이 증가하면 구조에서는 평형만으로 고유하게 결정되는 연속 구성을 사용합니다. 이러한 이유로 하중-변위 공간에 그려진 모든 곡선을 보다 정확하게 평형 경로라고 합니다. 자유도가 많은 구조에서는 하중의 강도가 달라지면 강성 매트릭스의 다양한 계수가 서로 다른 속도로 달라집니다. 따라서 적용된 하중에 대해 다른 변위 성분을 플로팅하여 얻은 평형 경로가 매우 다르게 보일 수 있습니다. 전체(일반화된) 비선형 반응이 실제로 (N+1) 차원 하중-변위 공간에서 표면이 되기 때문에 외관상 플로팅에 적합한 성분의 임의 선택이 적용됩니다. 여기서 N은 구조의 자유 변위 자유도 수입니다.
평형 방정식
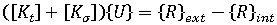
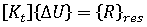
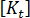 는 현재 구성에 대한 선형 강성 매트릭스입니다.
는 현재 구성에 대한 선형 강성 매트릭스입니다. 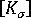 는 현재 구성에 대한 초기 응력 또는 지오메트리 강성 매트릭스입니다.
는 현재 구성에 대한 초기 응력 또는 지오메트리 강성 매트릭스입니다. 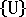 는 증분 절점 변위의 벡터입니다.
는 증분 절점 변위의 벡터입니다. 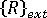 는 외부적으로 적용된 하중의 현재 레벨과 동등한 절점력의 벡터입니다.
는 외부적으로 적용된 하중의 현재 레벨과 동등한 절점력의 벡터입니다. 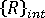 는 내부 응력 필드와 동등한 절점력의 벡터입니다.
는 내부 응력 필드와 동등한 절점력의 벡터입니다. 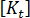 는 현재 구성에 대한 접선 강성 매트릭스입니다.
는 현재 구성에 대한 접선 강성 매트릭스입니다. 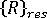 는 현재 구성에서 잔류(불균형) 절점력의 벡터입니다.
는 현재 구성에서 잔류(불균형) 절점력의 벡터입니다.
이러한 방정식은 비선형이며 직접 해결할 수 없습니다. 대신 좌변은 예측 변수로 사용되고 우변은 수정자로 사용되는 고전적 예측 수정자 반복 기술(예: Newton-Raphson 또는 준 Newton)을 사용할 수 있습니다. 일반적인 성공 반복 사이클 중에는 구조의 구성이 실제 평형 구성으로 수렴되는 동시에 잔류 불균형 힘 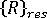 는임의로 작아집니다. 실제로 반복은 목표 정확도(프로그램이나 사용자에 의해 정의됨)에 도달하면 종료됩니다. 평형 반복 중에는 하중 레벨이 일반적으로 일정하게 유지됩니다.
는임의로 작아집니다. 실제로 반복은 목표 정확도(프로그램이나 사용자에 의해 정의됨)에 도달하면 종료됩니다. 평형 반복 중에는 하중 레벨이 일반적으로 일정하게 유지됩니다.
솔루션 방법
- KSTRA=0: 초기 강성 방법
-
비용은 저렴하지만 단순한 이 방법에서는 초기 선형 탄성 상수
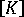 가 모든 부하 증분과 증분 내 각 반복 사이클에 사용됩니다(초기 강성 방법). 변위 증분의 예측이 항상 초기 지오메트리 기준으로 강성 매트릭스의 선형화를 기반으로 하므로 수렴이 매우 느릴 수 있으며 일반적으로 평형 경로에서 현저한 비선형이 발생하는 즉시 알고리즘이 실패하게 됩니다. 즉, 지정된 반복 횟수 내에서 수렴되지 않거나 확산됩니다.
가 모든 부하 증분과 증분 내 각 반복 사이클에 사용됩니다(초기 강성 방법). 변위 증분의 예측이 항상 초기 지오메트리 기준으로 강성 매트릭스의 선형화를 기반으로 하므로 수렴이 매우 느릴 수 있으며 일반적으로 평형 경로에서 현저한 비선형이 발생하는 즉시 알고리즘이 실패하게 됩니다. 즉, 지정된 반복 횟수 내에서 수렴되지 않거나 확산됩니다. 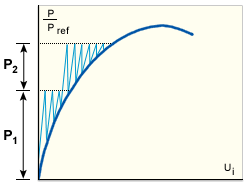
초기 강성 방법
- KSTRA=1: MNR(수정된 Newton-Raphson)
-
여기서는 각 부하 증분이 시작될 때, 즉 이전 단계(연화 구조에 대한 수정된 NR 방법 및 경화 구조에 대한 수정된 NR 방법)가 끝날 때 얻은 평형 구성에서 구조 강성 매트릭스가 업데이트되고 인수 분해됩니다. 그런 다음 강성을 개정하지 않고 반복이 수행됩니다. 이 전략은 약간 비선형인 평형 경로의 제품에 적합합니다.
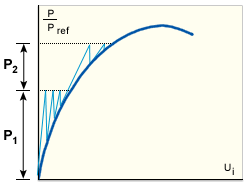
연화 구조에 대한 수정된 NR 방법
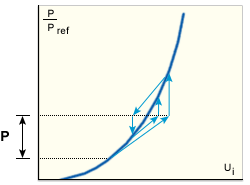
경화 구조에 대한 수정된 NR 방법
- KSTRA=2: NR과 MNR의 조합
-
이 방법은 MNR 방법을 수정한 것으로 강성이 각 단계가 시작될 때 개정되고 인수 분해되며 첫 번째 반복 후 다시 개정되고 인수 분해됩니다(경화 구조에 대해 조합 방법). 이 알고리즘은 중간 비선형을 처리할 수 있습니다.
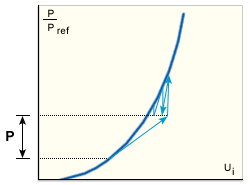
경화 구조에 대한 조합 방법
- KSTRA=3: NR(Newton-Raphson)
-
이 경우 구조 강성 매트릭스는 각 반복 사이클이 시작될 때 업데이트됩니다(전체 NR 접근방식). 이 방법은 신속한(2차 접근) 수렴을 보여주며 강력한 비선형 및 평형 경로의 분기를 처리하는 데 적합합니다. 그러나 지정된 횟수만큼 반복되는 동안 지금까지 살펴본 다른 방법 중에서 가장 많은 시간이 소요됩니다.
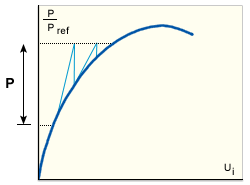
전체 NR 접근방식
- KSTRA=4: 단계가 감소된 NR(Newton-Raphson)
-
이 전략은 KSTRA=3과 동일하지만 KSTRA=3을 사용하여 수렴 문제가 발생하는 경우 순수한 NR 반복은 유지하면서 1/4의 단계 크기로 단계를 다시 수행하도록 도입되었습니다.
- KSTRA=5: 하중 단계
-
이 방법에서는 평형 반복이 일시적으로 억제됩니다. 따라서 각 부하 증분에 대해 구조 강성의 개정 및 축소가 한 번만 요구되며 반복이 사용되지 않습니다(간단한 하중 단계). 실제 평형 경로에서 이동을 최소화하려면 부하 증분이 MNR 또는 NR에서 사용된 것보다 훨씬 작고 불균형 힘이 손실되지 않고 다음 단계로 전달되어야 합니다. 이 방법은 다른 모든 전략이 실패한 경우 최후 수단으로만 사용됩니다.
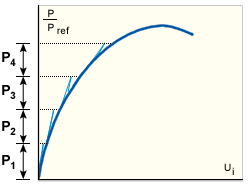
간단한 하중 단계
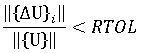
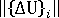 는 연속하는 두 반복 사이의 절점 변위 변화에 대한 유클리드 표준입니다. 즉, 다음과 같습니다.
는 연속하는 두 반복 사이의 절점 변위 변화에 대한 유클리드 표준입니다. 즉, 다음과 같습니다. 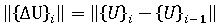
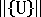 는 현재 총 절점 변위에 대한 유클리드 표준입니다. 사용할 RTOL의 적절한 값은 문제에 따라 어느 정도 달라지지만 0.01에서 0.0001 사이의 범위에 있는 값은 적절한 정밀도를 제공할 것으로 예측할 수 있습니다.
는 현재 총 절점 변위에 대한 유클리드 표준입니다. 사용할 RTOL의 적절한 값은 문제에 따라 어느 정도 달라지지만 0.01에서 0.0001 사이의 범위에 있는 값은 적절한 정밀도를 제공할 것으로 예측할 수 있습니다. 자동 제어 기술
비선형 유한 요소 해석의 주요 문제 중 하나는 단일 반복 방법이 전체 솔루션 경로에 가장 적합하지 않다는 것입니다. 경로의 비선형이 보다 심각해지면 선택한 전략이 수렴되지 않아 이후 진행이 불가능할 수 있습니다. 다른 단계 크기 및/또는 다른 전략을 사용하여 실패한 단계를 다시 수행할 수 있는 자동 제어 시스템만 있으면 됩니다. 이러한 구조는 해석에서 사용할 수 있으며 사용자 작업 없이 자동으로 솔루션 경로를 추적할 수 있도록 하려는 경우 매우 성공적인 것으로 확인되었습니다. 구조의 피처는 다음과 같습니다.
- 초기 최소 전략(일반적으로 KSTRA=1 또는 2) 및 초기 단계 크기를 선택합니다. 이 전략은 수렴 문제(있는 경우)가 발생될 때까지 유지됩니다.
- 다음과 같은 경우 수렴 문제가 발생한 것으로 간주됩니다.
- 허용된 최대 반복 횟수 Imax(기본값 또는 사용자가 지정) 내에서 수렴이 달성되지 않은 경우 또는
- 솔루션이 확산되는 경우(분기 솔루션은 4 이상의 반복에 대해 현재 변위 증분의 표준
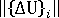 가 단계의 첫 번째 변위 증분의 표준
가 단계의 첫 번째 변위 증분의 표준 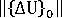 보다 큰 경우에 가정됩니다. 불균형 힘의 유클리드 표준은 적용된 하중의 유클리드 표준보다 큽니다.)
보다 큰 경우에 가정됩니다. 불균형 힘의 유클리드 표준은 적용된 하중의 유클리드 표준보다 큽니다.)
- 솔루션 방법은 KSTRA의 증가하는 값 순서로 정렬됩니다. 수렴 문제가 발생하는 경우 프로그램에서 다음 상위 전략을 사용하여 단계를 다시 수행합니다. 동시에 단계 크기는 이전 값의 1/4로 줄어듭니다. 이제 새 전략은 추가 수렴 문제가 발생할 때까지 유지되며, 이 경우 다음 상위 전략이 선택되고 단계 크기는 다시 줄어듭니다.
- 이 공정은 최대 단계 수에 도달하거나 하중이 허용되는 레벨을 초과할 때까지 계속됩니다. 이러한 변수는 모두 사용자가 조정할 수 있습니다.
- 다음과 같은 경우 처음에 선택한 전략보다 높은 상위 전략이 사용 중이면 다음 하위 전략으로 돌아가려고 시도합니다.
- 현재 전략의 네 개 단계(KSTRA = 1, 2, 3 또는 4)에 허용된 반복 횟수의 절반 이상이 필요하지 않은 경우 또는
- 현재 전략(KSTRA = 5)이 네 번 사용된 경우
선택한 하위 전략이 실패하면 이후 네 개 증분에 이전 방법이 사용되지만 단계 크기가 추가로 줄어들지 않습니다.
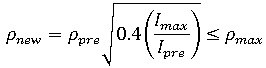
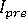 는 이전 단계에서 사용된 반복 횟수이고,
는 이전 단계에서 사용된 반복 횟수이고, 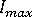 는 최대 반복 횟수이며,
는 최대 반복 횟수이며, 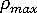 는 단계 크기 제한(사용자가 조정할 수 있음)입니다. 예를 들어
는 단계 크기 제한(사용자가 조정할 수 있음)입니다. 예를 들어 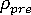 = 1,
= 1, 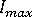 = 20,
= 20, 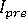 = 4 및
= 4 및 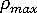 = 2이라고 가정하면 공식에서 현재 단계 크기가
= 2이라고 가정하면 공식에서 현재 단계 크기가 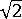 임을 확인할 수 있습니다.
임을 확인할 수 있습니다. 또한 수렴 실패가 발생하면 원래 단계 크기(즉, 실패한 증분에서 사용 중이던 단계 크기)가 복구되기 전에 각 단계에서 평균 4번 반복하여 네 단계를 수행한다는 것도 보여줍니다. 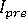 가
가 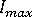 의 40%를 초과하면 비교적 느리지만 단계 크기가 축소됩니다.
의 40%를 초과하면 비교적 느리지만 단계 크기가 축소됩니다.