좌굴 해석

구조의 반응을 따르는 전체 비선형 증분/반복 방법은 아주 일반적이고 상대적으로 정확하지만 많은 계산 노력이 수반될 수도 있습니다.

좌굴의 기본적인 중요성 및 설계의 함축적 의미로 인해 좌굴이 발생할 것으로 예상되는 임계 하중 레벨에 대해 근사치를 제공하는 간단한 방법이 분명히 중요합니다. 좌굴 전 반응이 선형이고 좌굴 전 변위의 효과를 무시할 수 있다고 가정하는 경우 이러한 방법을 연구할 수 있습니다. 좌굴 해석이라고 하는 이 방법은 초기 안정성 또는 고전적 분기 해석이라고도 합니다.

다음 섹션에서는 일반화된 좌굴 해석 방법에 대해 설명한 다음 이 해석에서 사용하는 두 가지 특정 방법에 대해 설명합니다.

일반화된 좌굴 해석

좌굴 해석의 목표는 적용된 하중의 몇 가지 알려진 분포 {P}에 대한 임계 좌굴 하중을 확인하는 것입니다. 따라서 정의에 따라 다음과 같이 작성할 수 있습니다.

여기에서 각 항목은 다음과 같습니다.

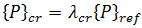
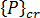• 은 적용된 하중 분포의 임계 레벨입니다.
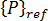• 는 동일한 하중 분포(기준 하중)의 임의 레벨입니다.
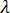• 는 스칼라 승수입니다.

이러한 정의에서는 하중 승수 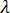_{가 임계값 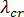에 도달하면 좌굴이 발생합니다. 좌굴 해석의 시작점은 강성 매트릭스의 각 계수 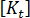가 적용된 하중에 따라 선형으로 변한다는 가정입니다. 위에서 설명한 대로 적용된 하중을 일부 변수(예: 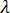)에 일정한 힘 벡터 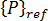를 곱한 것으로 생각할 수 있습니다.}

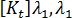구조의 두 가지 알려진 상태( 그리고 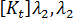)와 선형성 가정이 지정된 경우 지정된 평형 구성의 강성 매트릭스 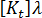는 다음과 같이 지정됩니다.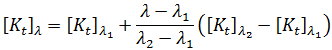

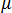분수 항을 로 정의하고 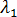에서 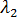로의 강성 변화를 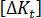로 정의하면 다음과 같습니다.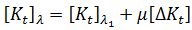

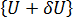특정 좌굴 점에 두 가지 평형 구성 {U}와 가 있고 둘 다 하중 레벨이 동일합니다.

아래 그림에 표시된 대로 두 가지 기본 좌굴 유형(자세한 내용은 뒷부분에서 설명)의 평형 구성을 보여줍니다.

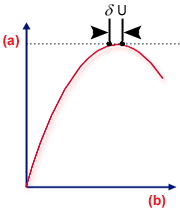
제한점

.

(a) 하중, (b) 변형

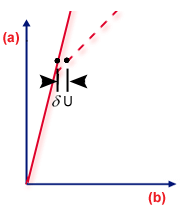
분기점

.

(a) 하중, (b) 변형

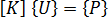선형 해석의 기본 방정식 를 사용하여 다음과 같이 작성할 수 있습니다.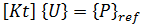

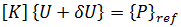
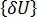여기에서 각 항목은 다음과 같습니다. {U}는 하중에 해당하는 변위입니다. {P] 및 는 두 평형 구성 간의 매우 작은 변위를 나타냅니다. 두 번째 방정식에서 첫 번째 방정식을 빼면 다음과 같습니다.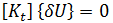

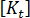여기에서 각 항목은 다음과 같습니다. 는 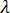의 함수입니다. 선형 대수에서는 위의 방정식을 풀면 다음 방정식을 푸는 것과 동일합니다.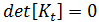

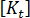따라서 좌굴은 의 결정 인자가 0일 때 발생합니다. 그 결과 일반화된 좌굴 문제에 대해 해결할 방정식은 다음과 같으며, 이 방정식은 고유 문제이고 확인되지 않은 것으로 알려져 있습니다. 위의 방정식은 표준 방법(예: 부분 공간 반복)으로 해결할 수 있습니다.

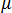의 정의를 다시 배열하여 다음을 찾을 수 있습니다.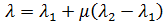

이 방정식은 좌굴을 발생시키는 데 필요한 하중 승수를 알려줍니다. 이 해석은 이 일반 방법의 두 가지 단순화를 사용하는데, 이를 선형(고전적) 좌굴 해석 및 선형화된 좌굴 해석이라고 합니다.

선형(고전적) 좌굴 해석

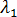이 방법에서는 = 0 및 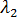= 1을 선택합니다. 즉, 0과 전체 적용된 하중을 기준 상태로 사용합니다. 이런 경우 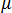가 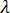로 줄어 방정식이 다음과 같이 됩니다.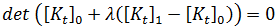

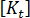업데이트된 라그랑주 이론에서는 를 두 개의 성분으로 분할할 수 있습니다.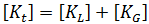

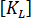여기에서 각 항목은 다음과 같습니다. 은 1차 강성 매트릭스이고 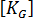는 더 높은 차수의 강성 매트릭스(응력 또는 지오메트리 매트릭스라고도 함)입니다. 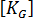는 재료 응력 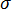의 선형 함수입니다.

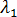처음에 제품에 응력이 없는 경우 =0은 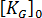=0을 의미합니다. 따라서 다음과 같이 됩니다.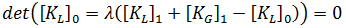

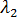고전적 방법의 주요 가정은 최대 =1에 대한 반응이 순수 선형, 즉 응력 및 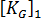이 원래 좌표를 사용하여 평가된다는 것입니다. 고전적 방법의 또 다른 가정은 강성의 1차 부분이 하중과 함께 변경되지 않아 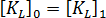이라는 것입니다. 총 라그랑주 용어에서 이 가정은 "변위-매트릭스" 효과를 무시하는 것과 동일합니다. 따라서 위의 방정식이 다음과 같이 줄어듭니다.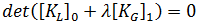

선형 좌굴 방법은 변형의 초기 조건에 기반하지 않는 구조 또는 변형 해석에 사용됩니다. 경험에 의하면 변형 문제의 고전적 좌굴 해석에서는 좌굴 하중을 정확하게 예측합니다. 고전적 방법은 좌굴 전 형상의 변화가 거의 없기 때문에, 즉 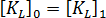이 적합한 근사치이기 때문에 제대로 작동합니다.

선형화된 좌굴 해석

이 방법에서는 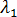= 0 및 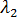( 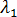에 매우 가까움)를 선택합니다. 즉, 0과 하중의 매우 작은 분율을 기준 상태로 사용합니다. 매우 작은 단계만 수행하므로 평형 반복이 필요하지 않고 해석에서는 전략 5를 사용하여 단계를 수행합니다.

또한 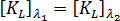를 가정합니다. 이 방법에서는 응력이 업데이트된 좌표를 사용하여 평가됩니다.

이제 방정식이 다음과 같이 됩니다.

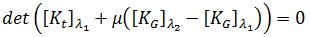
응력 전 성분을 해석하는 가장 간단하고 가장 빠른 방법은 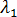= 0 및 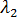= 0.001을 사용하는 것입니다. 따라서 한 단계만 수행하면 되고 평형 반복이 수행되지 않으므로 솔루션 비용이 고전적 방법의 비용보다 약간만 더 큽니다.

선형화된 좌굴 방법은 변형 해석의 초기 조건을 기반으로 하는 구조 해석에만 사용됩니다. 고전적 방법은 공정에서 상당한 잔류 응력이 생성되므로 이러한 문제에 적용할 수 없습니다. 이는 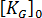= 0이라는 가정을 위반합니다. 대신 선형화된 좌굴 방법을 사용해야 합니다. 이는 초기 조건 좌굴 해석을 선택할 때 응력으로 표시됩니다.