자유도가 매우 작은 문제의 경우 결정 인자가 명시적으로 평가되어 N 차수의 다항식을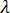 
에서 지정할 수 있습니다. 여기서 N은 구속조건이 지정되지 않은 자유도의 수입니다.
N 실근이 있고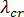 
는 가장 작은 크기의 근과 같으면 됩니다. 좌굴 방정식에 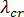를 후방 대입하면 중요 좌굴 변위 모드가 지정됩니다. 이 모드는 좌굴 중 발생하는 구성 변경에 해당하는 변위의 임의 배율 조정된 세트로 정의됩니다. 따라서 구조의 좌굴 후 구성을 보려는 경우 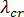와 관련된 중요 변위 모드를 구조의 변형되지 않은 구성 위에 겹쳐야 합니다.
자유도가 많은 구조의 경우 결정 인자 팽창 다음에 오는 근 추출 방법이 작동하지 않을 수 있습니다. 보다 일반적인 솔루션 알고리즘을 사용하려면 일반화된 고유 값 문제로 좌굴 방정식을 식별해야 합니다. 이 고유 값 문제와 관련하여 N개의 실수 고유 쌍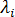 
, 
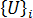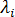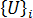이 있습니다. 여기서 i = 1,...N, 및 는 각각 i번째 고유 값과 i번째 임계 하중 계수 및 좌굴 변위 모드를 나타내는 고유 벡터입니다. 강력한 범용 방법을 사용하여 일반화된 고유 값 문제를 해결할 수 있습니다. 사용된 방법을 부분 공간 반복 방법[1]이라고 합니다.
부분 공간 반복 방법을 사용하여 일련의 n 고유 쌍을 찾을 수 있으며, 이 고유 쌍은 증가하는 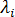크기 순서로 배열됩니다. 즉,
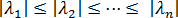순서이고 =
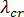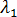그리고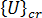 
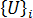= 를 따릅니다.
찾으려는 고유 값 수는 변형 또는 응력 해석 중에 지정할 수 있는 변수입니다. 그러나 필요한 고유 쌍 솔루션 수가 증가할수록 관련된 계산 노력도 현저하게 증가합니다. 또한 좌굴 문제에서는 일반적으로 가정상 더 높은 차수의 모드가 아니라 "실제" 중요 상태에만 관심이 있습니다. 일반적으로 하중이 증가하면 구조가 첫 번째 중요 모드에서 다른 더 높은 차수 모드로 변경(일반적으로 분기 사용)되지만 더 높은 차수 모드에 해당하는 하중 레벨 및 좌굴 형상이 예측된 첫 번째 모드와 의미 있게 관련이 있다고 가정하는 것은 매우 잘못된 것이며 위험합니다. 그 이유는 더 낮은 좌굴 모드에서 더 높은 좌굴 모드로 전환하는 동안 구조의 구성이 현저하게 변경될 수 있으므로 좌굴 해석의 기본 가정과 명백하게 충돌하기 때문입니다.
예측 고유 값의 부호
값 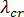에는 제한이 없으며 양수 값과 음수 값을 모두 사용할 수 있습니다. 예를 들어 평면 플레이트에 인장 응력 필드를 만들도록 
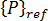를선택하면 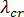는 음수가 됩니다. 그러나 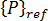의 방향을 반전하여 응력 상태를 압축하면 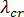가 양수 값이 됩니다. 그러나 정의상으로 두 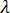값은 크기가 정확하게 동일합니다. 기준 하중 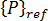를 되돌리면 실제로 첫 번째 고유 쌍만 찾을 수 있습니다. 이는 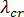가 음수인 경우 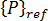의 방향을 반전하면 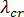부호가 반전됨을 알고 있기 때문입니다. 그러나 반전할 수 없는 하중 시스템을 고려하면 문제가 발생합니다. 이 경우 좌굴은 가장 작은 양수 고유 값에 해당하며, 얼마나 많은 음수 고유 값이 있는지 미리 알 수 없으므로 시행착오를 겪거나 둘 이상의 고유 쌍이 요청되는 단일 해석을 수행해야 합니다. 반전할 수 없는 하중 시스템의 날짜 환경(예: 플라스틱 성분에서 작용하는 수축 변형)은 처음 두 고유 쌍에 대한 솔루션이 일반적으로 충분함을 나타냅니다. 즉, 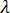값이 둘 다 양수이거나 하나는 음수이고 하나는 양수임을 나타냅니다.
Sturm 시퀀스 확인
부분 공간 반복 방법을 사용하면 경우에 따라 하나 이상의 고유 값을 생략할 수 있는데, 실제로 존재하는 하나 이상의 고유 값이 예측된 값에서 누락될 수 있기 때문입니다. 따라서 Sturm 시퀀스 확인이라는 기술을 사용하여 누락된 고유 값을 확인합니다. 안타깝게도 n 고유 값이 음수인 경우에는 확인이 유효하지 않습니다.
좌굴 결과의 유효성
좌굴 해석을 수행하는 경우 초기 가정의 제한적 특성을 기억해야 합니다. 좌굴 이전에 형상이 크게 변경되는 경우 방법이 유효성의 범위 외부에 적용되므로 결과를 신뢰할 수 없게 됩니다. 일반적으로 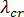가 과대 평가되지만 항상 그렇지는 않음을 의미합니다. 구조의 좌굴 전 변위가 작지 않다고 판단되는 경우 항상 좌굴 해석을 수행한 다음 전체 대변형 해석을 수행해야 합니다.
좌굴의 유형
-
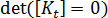
제한점
-
분기
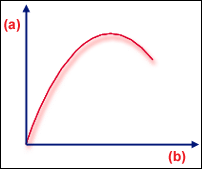
제한점
.(a) 하중, (b) 변형
완벽한 구조의 분기
.(a) 하중, (b) 변형
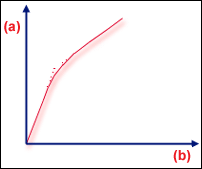
실제 구조의 분기
.(a) 하중, (b) 변형
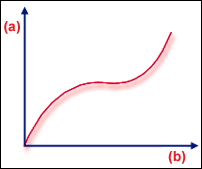
연화 후 경화
.(a) 하중, (b) 변형
제한점은 형상을 크게 변경하지 않고는 성분에서 더 이상 하중을 허용할 수 없는 상태입니다(제한점). 일반적으로 중심 하중으로 인해 돔이 "스냅스루"될 수 있는 돔 형상 성분에서 발생합니다. 보다 일반적으로 좌굴 점 앞에 현저한 지오메트리 비선형성이 있는 경우 좌굴이 제한점이 될 것으로 예측합니다. 돔 예제에서는 강성 매트릭스 결정 인자가 0이 되기 전에 성분이 완전히 납작해져야 합니다. "스냅스루"(부드럽거나 엄격할 수 있음) 후 성분은 더 많은 하중을 허용할 수 있지만 일반적으로 예상 하중이 제한점에 도달하지 않도록 성분을 설계해야 합니다.
분기는 두 개의 가능한 평형 상태가 함께 가깝게 배치되는 "분기" 점입니다. 완벽하게 대칭인 평판 플레이트를 고려할 경우 평면 압축 하중에 대한 플레이트의 반응은 단순히 선형입니다. 그러나 하중이 중요한 값을 초과하면 평형이 불안정해져 어떤 방향으로 굴러 떨어질지를 예측할 수 없는 언덕 꼭대기의 공과 같습니다. 그러므로 실제 평판 플레이트는 해당 임계 하중 레벨에서 좌굴됩니다. 따라서 두 개의 평형 경로가 있을 수 있고 해당 교차점을 "분기점"(완벽한 구조의 분기)이라고 합니다.
분기는 더 일반적이지만 이러한 유형의 좌굴은 모두 변형이나 열 하중 문제에서 나타날 수 있습니다. 평판 플레이트 예제에서 플레이트의 결점으로 인해 분기점(완벽한 구조의 분기)에서 강성이 급격하게 변경되는 블러가 발생할 수 있습니다. 또 다른 일반적인 반응은 "연화 후 경화"(연화 후 경화)입니다. 이 경우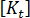 
의 결정 인자는 0이 아니라 몇 가지 작은 값이 됩니다.
완벽한 구조의 분기 및 실제 구조의 분기와 같은 사례의 좌굴 해석은 일반적으로 분기의 위치를 잘 나타냅니다. 제한점과 같은 사례의 해석은 제한점을 과도하게 예측하는 경향이 있습니다. 연화 후 경화와 같은 문제에는 명확한 좌굴 하중이 없지만 좌굴 해석은 종종 비선형성이 심각해지기 시작하는 위치를 나타냅니다.
참조 문헌
1. Bathe, K.J., Finite Element Procedures in Engineering Analysis, Prentice-Hall, Englewood Cliffs, New Jersey, 1982, pp. 666-696.