미드플레인 및 Dual Domain 해석 기술의 경우 구조 해석에서 쉘 및 빔 요소를 모두 제공합니다.
쉘 요소
쉘 요소는 평면 직선 모서리 삼각형 형식입니다. 곡선 쉘을 모델링하면 실제 지오메트리에 "면처리" 근사치를 제공합니다. 현재 각 요소의 두께는 일정한 것으로 가정되지만 인접한 요소의 두께는 다를 수 있습니다.
어떤 경우든 각 절점에서 6개의 변위 자유도가 사용됩니다. 여기에는 전역 축에 평행인 변위 세 개와 이러한 축을 기준으로 하는 회전 세 개가 포함됩니다. 평탄한 쉘의 경우 변위 세 개와 중간 면 법선의 지역 회전 두 개인 5개의 자유도만 사용할 수 있습니다. 그러나 어떤 경우든 6개의 자유도를 사용하면 고유한 장점이 있습니다. 먼저 간섭하는 면 사이의 접합부에 특별한 구속조건을 적용하지 않고 상자, 트레이 및 경화된 쉘과 같은 평탄하지 않은 구조를 해석할 수 있습니다. 두 번째로 구속조건이나 변형을 적용하지 않고 기본 플레이트나 쉘 메쉬의 절점에 빔 요소(3차원 공간에서 6개의 자유도가 있어야 함)를 직접 부착할 수 있습니다. 세 번째로 대변형(기하학적으로 비선형) 해석에서 회전 자유도 세 개를 사용하면 유한 강체 모션에 대해 멋지고 기하학적으로 정확한 모델을 만들 수 있습니다[1-3]. 얇은 벽 구조의 기존 지오메트리 비선형 모델에서 나타나는 많은 결함은 회전 변수를 기준으로 하는 근사치에서 기인한다는 점에 주의해야 합니다. 여기서 적용된 변수는 연관된 회전 텐서의 스펙트럼 해석과 직접 관련된다는 점에서 "자연적"입니다. 선형화된 양식을 얻으려면 Euler 및 Rodriques가 제안한 강체 운동학의 고전적 해석을 사용해야 합니다[1,3,4].
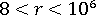
잠금 제거와 별도로 이 방법은 얇은 쉘의 감도를 요소 뒤틀림으로 줄이고 강성 매트릭스의 조절 및 응력 예측의 품질을 향상시킵니다.
현재 선형 탄성 재료만 모델링할 수 있습니다. 이러한 재료는 등방성이거나 직교 이방성일 수 있습니다. 후자에서는 재료의 기본 평면이 직각이어서 한 평면은 쉘의 중간 면에 놓여 있고 이 면을 교차하는 다른 두 평면은 직교 이방성의 방향이라고 하는 두 수직선을 따릅니다. 직교 이방성의 방향은 공정에 의해 결정되며 충전+보압 해석에서 각 요소에 대해 규정됩니다. 각 방향에서 재료 속성은 사용자가 변형 또는 응력 해석에 대한 해석 입력 파일을 준비할 때 지정합니다.
지오메트리 비선형성은 변위 필드를 각 점에서 쉘의 단면과 동시 회전하는 지역 대류 좌표 세트라고 하는 대류된 라그랑주 접근방식을 기반으로 합니다. 일관성을 위해 여기서는 모든 점에서 단면 디렉터와 동일선상에 있는 섬유에 일반적인 불확장 조건을 적용합니다.
이 동시 회전 방법은 일반적인 공간 모션이 항상 순수 신장력(변형)으로 분해된 다음 강체 모션으로 분해된다고 주장하는 연속체 역학의 극좌표 분해 정리에서 파생됩니다. 적합한 유한 회전 측정값(위 참조)을 적용하고 전체 모션에서 강체 성분을 명시적으로 버리면 요소 내에서 내부 변형 및 관련된 응력을 일관된 방법으로 평가할 수 있습니다. 실제로 강체 모션의 크기를 제한할 필요가 없으며 내부 변형과 응력이 결정되는 정밀도가 해석 전체에서 일정하게 유지된다는 의미입니다.
이 형식화는 Reissner[11,12]의 유한 변형 이론, Simmonds 및 Danielson[13], Danielson 및 Hodges[14], Bates[1] 및 Simo와 Vu-Quoc[15]에 의한 이러한 이론의 유한 요소 구현과 밀접한 관련이 있습니다.
- 요소 LMT3
-
LMT3 요소는 미드플레인 해석 기술에서 사용됩니다. LMT3은 자유도가 18개(각 절점에 6개씩)인 3절점 삼각형 요소입니다. 이 요소는 Bergan 및 Nygard[16]와 Bergan 및 Felippa[17]의 지역 멤브래인 형식화와 Tessler 및 Hughes[10]의 벤딩 형식화를 결합하고 결합된 방정식을 전역 좌표 시스템으로 변형하여 구성됩니다. 결과 요소는 멤브래인 및 횡방향 전단 변형의 쌍일차 변형을 모델링할 수 있지만 굴곡 방향 변형(곡률)은 일정합니다.
Bergan 및 Nygard의 "자유 형식화"는 가정된 변위 필드를 기반으로 하지만 "부적절한" 형상 함수를 사용할 수 있는 경우 엄격한 잠재 에너지 형식화 수준을 뛰어넘습니다. 수렴을 보장하기 위해 패치 테스트 요구사항이 선험적으로 적용됩니다. 변위 형상 함수는 기본 모드와 더 높은 차수 모드로 구분되는데, 전자는 강체 및 일정한 변형 상태와 관련되고 후자는 좌표 불변 평면 벤딩 모드와 관련됩니다.
따라서 기본 강성과 더 높은 차수 강성이 각각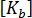 및
및 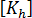 로 표시됩니다. 결합된 멤브래인 강성은 다음 형식을 사용합니다.
로 표시됩니다. 결합된 멤브래인 강성은 다음 형식을 사용합니다. 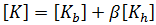
여기에서 각 항목은 다음과 같습니다.
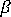 는 더 높은 차수 강성에서 배율로 사용되는 자유 변수입니다. 상세한 테스트 결과에 따라
는 더 높은 차수 강성에서 배율로 사용되는 자유 변수입니다. 상세한 테스트 결과에 따라 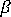 = 1.5는 최상의 선택으로 적용된 것입니다. 지역 중간 면 법선 기준 회전(드릴링 자유도라고도 함)은 페널티 구속조건 기술에 의해 중간 면의 평균 평면 회전에 연결됩니다. 따라서 다음과 같이 표시됩니다.
= 1.5는 최상의 선택으로 적용된 것입니다. 지역 중간 면 법선 기준 회전(드릴링 자유도라고도 함)은 페널티 구속조건 기술에 의해 중간 면의 평균 평면 회전에 연결됩니다. 따라서 다음과 같이 표시됩니다.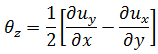
드릴링 자유도는 형식화에서 완전히 통합된 활성 성분입니다.
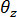 와 평면 구배 간 링크의 강도는 정확히 동일 평면상에 있는 요소의 경우 균등하게 유지되므로 특이성 문제가 더 이상 발생하지 않습니다.
와 평면 구배 간 링크의 강도는 정확히 동일 평면상에 있는 요소의 경우 균등하게 유지되므로 특이성 문제가 더 이상 발생하지 않습니다. 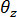 를 경계 조건 성분으로 사용할 경우 주의해야 합니다.
를 경계 조건 성분으로 사용할 경우 주의해야 합니다. 요소 벤딩 형식화의 기반은 연속 횡방향 전단 모서리 구속조건[10]을 통해 얻은 명시적 자유도 기술입니다. 구속된(연결형) 총 변위 필드에서 횡변위 uz의 4차 변형과 법선 회전
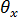 및
및 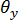 의 쌍일차 변형이 발생됩니다. 횡방향 전단 수정 계수 기술[10]과 결합될 경우 요소는 광범위한 면비 전체에서 표준 일정 곡률 형식화에 비해 훨씬 향상된 굴곡 방향 반응을 보여줍니다.
의 쌍일차 변형이 발생됩니다. 횡방향 전단 수정 계수 기술[10]과 결합될 경우 요소는 광범위한 면비 전체에서 표준 일정 곡률 형식화에 비해 훨씬 향상된 굴곡 방향 반응을 보여줍니다. - 요소 정의
-
요소에 대한 지오메트리, 절점 번호 매기기 및 지역/전역 자유도는 LMT3 쉘 요소에 표시되어 있습니다. 절점 i, j, k는 해석 출력 파일에 제공된 절점 연결성 표의 항목을 나타냅니다. 예를 들어 요소의 연결성이 11, 101, 85이면 i = 11, j = 101, k =85이고 지역 X축은 절점 11에서 절점 101까지 이어집니다.
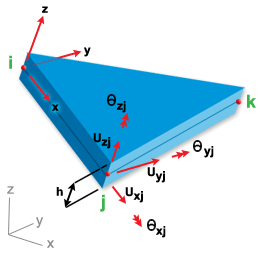
LMT3 쉘 요소
- 요소 하중
-
압력 하중과 직교 이방성 수축으로 인한 초기 변형이라는 두 가지 유형의 요소 하중을 사용할 수 있습니다.
압력 하중은 요소 중간 면에서 동작하고 해당 면에 대한 법선인 것으로 가정됩니다. 압력은 지정된 요소에 대해 일정한 값을 갖는 것으로 가정되지만 인접한 요소에서 사용되는 압력은 다를 수 있습니다.
- 통합 규칙
-
중간 면에 대한 통합은 3점 수치 구적을 사용하여 수행됩니다. 재료는 선형 탄성이고 요소는 편평하므로 변형과 응력 모두 전단 벽을 통해 선형으로 달라집니다. 따라서 비용이 더 많이 드는 수치 통합이 아니라 두께 방향의 명시적 사전 통합이 사용됩니다.
통합 측점 위치 및 중량은 LMT3 요소의 통합 측점 위치 및 LMT3 요소의 통합 위치 중량에 표시되어 있습니다.
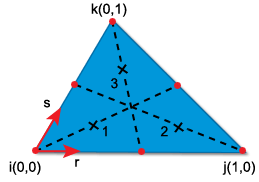
LMT3 요소의 통합 측점 위치
LMT3 요소의 통합 측점 중량 요소 통합 측점 r 좌표 s 좌표 LMT3 1
2
3
1/6
2/3
1/6
1/6
1/6
2/3
- 결과 출력
-
멤브래인 힘
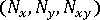 , 벤딩 모멘트
, 벤딩 모멘트 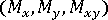 및 횡방향 전단력
및 횡방향 전단력 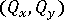 는 통합 측점에서 계산되고 LMT3 요소에 대한 해석 결과에 표시됩니다.
는 통합 측점에서 계산되고 LMT3 요소에 대한 해석 결과에 표시됩니다. 이러한 결과는 해석 출력 파일로 재현됩니다.
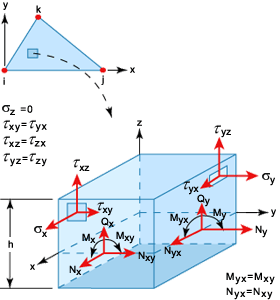
LMT3 요소에 대한 해석 결과
평면 응력 조건을 가정할 경우 모든 z 레벨의 응력은 다음과 같이 지정됩니다.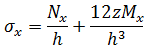
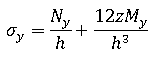
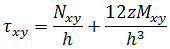
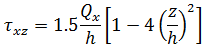 힘과 모멘트는 플레이트나 쉘의 유닛 너비로 작용하므로 멤브래인 힘과 전단력에는 치수 힘/길이가 있지만 모멘트에는 치수(힘)가 있습니다.
힘과 모멘트는 플레이트나 쉘의 유닛 너비로 작용하므로 멤브래인 힘과 전단력에는 치수 힘/길이가 있지만 모멘트에는 치수(힘)가 있습니다.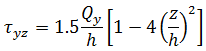
- 요소 LBT3
-
LBT3 요소는 Dual Domain 해석 기술에서 사용됩니다. LBT3은 자유도가 18개(각 절점에 6개씩)인 3절점 삼각형 요소입니다. 이 요소는 Bergan 및 Nygard와 Bergan 및 Felippa의 지역 멤브래인 형식화와 Batoz의 벤딩 형식화를 결합하고 결합된 방정식을 전역 좌표 시스템으로 변형하여 구성됩니다. 결과 요소는 멤브래인, 굴곡 방향 변형 및 횡방향 전단 변형의 쌍일차 변형을 모델링할 수 있습니다.
Bergan 및 Nygard의 "자유 형식화"는 가정된 변위 필드를 기반으로 하지만 "부적절한" 형상 함수를 사용할 수 있는 경우 엄격한 잠재 에너지 형식화 수준을 뛰어넘습니다. 수렴을 보장하기 위해 패치 테스트 요구사항이 선험적으로 적용됩니다. 변위 형상 함수는 기본 모드와 더 높은 차수 모드로 구분되는데, 전자는 강체 및 일정한 변형 상태와 관련되고 후자는 좌표 불변 평면 벤딩 모드와 관련됩니다.
따라서 기본 강성과 더 높은 차수 강성이 각각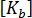 및
및 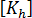 로 표시됩니다. 결합된 멤브래인 강성은 다음 형식을 사용합니다.
로 표시됩니다. 결합된 멤브래인 강성은 다음 형식을 사용합니다. 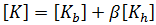
여기에서 각 항목은 다음과 같습니다.
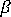 는 더 높은 차수 강성에서 배율로 사용되는 자유 변수입니다. 상세한 테스트 결과에 따라
는 더 높은 차수 강성에서 배율로 사용되는 자유 변수입니다. 상세한 테스트 결과에 따라 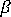 = 1.5는 최상의 선택으로 적용된 것입니다. 중간 면 법선 기준 회전(드릴링 자유도)은 LMT3에 사용된 것과 동일한 연속체 역학을 사용합니다. 즉, 다음과 같습니다.
= 1.5는 최상의 선택으로 적용된 것입니다. 중간 면 법선 기준 회전(드릴링 자유도)은 LMT3에 사용된 것과 동일한 연속체 역학을 사용합니다. 즉, 다음과 같습니다.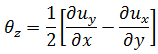
요소의 벤딩 형식화는 횡방향 전단 효과를 포함하는 불연속 Kirchhoff 기술의 일반화를 기반으로 합니다. 이 요소는 잠금이 없으며 두껍거나 얇은 제품의 해석에 유효합니다. 이 요소는 횡방향 전단 효과가 중요하지 않은 경우 잘 알려진 DKT(불연속 Kirchhoff 삼각형) 요소와 일치합니다.
수치 테스트에 따르면 LBT3은 매우 잘 수행됩니다. 일반적으로 LBT3이 LMT3보다 약간 더 우수합니다. 또한 LBT3에서는 단일 레이어와 다중 레이어 형식화를 모두 사용할 수 있지만 LMT3은 현재 단일 레이어 해석에만 유효합니다.
섬유 충전 플라스틱의 응력 및 변형 해석을 수행하려면 다중 레이어 LBT3을 사용하는 것이 좋습니다. 레이어별로 섬유 배향을 고려하는 경우 물리적 모델이 더 현실적이고 결과가 더 정확하게 예측됩니다.
- 요소 정의
-
요소에 대한 지오메트리, 절점 번호 매기기 및 지역/전역 자유도는 LBT3 쉘 요소에 표시되어 있습니다. 절점 i, j, k는 해석 출력 파일에 제공된 절점 연결성 표의 항목을 나타냅니다. 예를 들어 요소의 연결성이 11, 101, 85이면 i = 11, j = 101, k =85이고 지역 X축은 절점 11에서 절점 101까지 이어집니다.

LBT3 쉘 요소
- 요소 하중
-
압력 하중과 직교 이방성 수축으로 인한 초기 변형이라는 두 가지 유형의 요소 하중을 사용할 수 있습니다.
압력 하중은 요소 중간 면에서 동작하고 해당 면에 대한 법선인 것으로 가정됩니다. 압력은 지정된 요소에 대해 일정한 값을 갖는 것으로 가정되지만 인접한 요소에서 사용되는 압력은 다를 수 있습니다.
- 통합 규칙
-
중간 면에 대한 통합은 3점 수치 구적을 사용하여 수행됩니다. 재료는 선형 탄성이고 요소는 편평하므로 변형과 응력 모두 전단 벽을 통해 선형으로 달라집니다. 따라서 비용이 더 많이 드는 수치 통합이 아니라 두께 방향의 명시적 사전 통합이 사용됩니다.
통합 측점 위치 및 중량은 LBT3 요소의 통합 측점 위치 및 LBT3 요소의 통합 위치 중량에 표시되어 있습니다.

LBT3 요소의 통합 측점 위치
LBT3 요소의 통합 위치 중량 요소 통합 측점 r 좌표 s 좌표 LBT3 1
2
3
1/6
2/3
1/6
1/6
1/6
2/3
- 결과 출력
-
멤브래인 힘
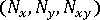 , 벤딩 모멘트
, 벤딩 모멘트 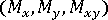 및 횡방향 전단력
및 횡방향 전단력 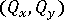 는 통합 측점에서 계산되고 LBT3 요소에 대한 해석 결과에 표시됩니다.
는 통합 측점에서 계산되고 LBT3 요소에 대한 해석 결과에 표시됩니다. 이러한 결과는 해석 출력 파일로 재현됩니다.

LBT3 요소에 대한 해석 결과
평면 응력 조건을 가정할 경우 모든 z 레벨의 응력은 다음과 같이 지정됩니다.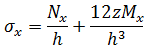
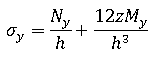
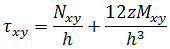
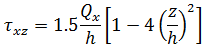
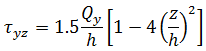
힘과 모멘트는 플레이트나 쉘의 유닛 너비로 작용하므로 멤브래인 힘과 전단력에는 치수 힘/길이가 있지만 모멘트에는 치수(힘)가 있습니다.
빔 요소
2절점 빔인 빔 요소 BEAM2는 현재 미드플레인과 Dual Domain 해석 기술 모두에서 사용할 수 있습니다.
요소의 세로 축이 직선이므로 곡선 빔을 모델링하면 실제 지오메트리에 "면처리" 근사치를 제공합니다. 현재 빔은 반지름이 일정한 원형 단면이 있는 것으로 가정됩니다. 그러나 인접한 요소의 단면 반지름은 다를 수 있습니다.
각 절점에서 6개의 자유도가 사용됩니다. 즉, 전역 축에 평행인 변위 세 개와 이러한 축을 기준으로 하는 회전 세 개가 사용됩니다. 유한 회전 컨텍스트에서 회전 자유도는 쉘에 대해 설명한 정의와 정확하게 동일합니다. 하나 이상의 절점에서 빔과 쉘 요소의 물리적 연결은 간단합니다. 모든 빔 절점이 쉘 절점에 연결되어 있으면 결합된 구조를 모델링하는 데 필요한 총 방정식 수가 쉘 구조를 자체적으로 모델링하는 데 필요한 개수와 동일합니다. 따라서 빔 요소 추가와 관련된 계산 오버헤드가 일반적으로 매우 작습니다.
요소 형식화는 축, 벤딩, 비틀림 및 횡방향 전단 변형을 고려합니다. 기본 가정은 빔 단면이 뒤틀리지 않고 평면으로 유지되지만 횡방향 전단이 있으면 세로 축에 대한 법선으로 유지되지 않는다는 것입니다. 결과 모델은 두 단계의 고전적 Euler-Bernoulli 빔에서 파생되는 것으로 간주할 수 있습니다. 먼저 횡방향 전단의 평균 효과는 Reissner-Mindlin 유형 전단 모델을 추가하여 고려합니다. 그러면 일반적으로 Timoshenko 빔이라고 하는 빔이 생성됩니다. 두 번째 단계에서는 St.Venant의 이론을 사용하여 비틀림 동작을 모델링합니다.
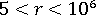
페널티 이완 기술을 사용하여 상한을 매우 높게 지정할 수 있습니다. 빔 요소는 전단이나 멤브래인 잠금의 영향을 받지 않지만 이 기술은 높은 면비에서 요소 강성 매트릭스가 까다롭게 되는 것을 방지합니다.
현재 빔 요소에 대해 등방성 선형 탄성 재료만 모델링할 수 있습니다. 위에서 설명한 기본 가정과 충돌하지 않으면 일반적인 직교 이방성 재료 동작은 고려할 수 없습니다.
지오메트리 비선형성은 변위 필드를 각 점에서 쉘의 단면과 동시 회전하는 지역 대류 좌표 세트라고 하는 대류된 라그랑주 접근방식을 기반으로 합니다. 일관성을 위해 여기서는 모든 점에서 단면 디렉터와 동일선상에 있는 섬유에 일반적인 불확장 조건을 적용합니다.
이 동시 회전 방법은 일반적인 공간 모션이 항상 순수 신장력(변형)으로 분해된 다음 강체 모션으로 분해된다고 주장하는 연속체 역학의 극좌표 분해 정리에서 파생됩니다. 적합한 유한 회전 측정값을 적용하고 전체 모션에서 강체 성분을 명시적으로 버리면 요소 내에서 내부 변형 및 관련된 응력을 일관된 방법으로 평가할 수 있습니다. 즉, 강체 모션의 크기를 제한할 필요가 없으며 내부 변형과 응력이 결정되는 정밀도가 해석 전체에서 일정하게 유지된다는 의미입니다.
이 형식화는 Reissner[11], Danielson 및 Hodges[14], Hodges 및 Simo의 유한 변형 이론과 밀접한 관련이 있습니다. Bates[1]와 Simo 및 Vu-Quoc[15]에 의한 이러한 이론의 유한 요소 구현도 관련이 있습니다.
- 요소 BEAM2
-
이 요소는 각 절점에 6개의 자유도가 있는 2절점 빔입니다. 빔 축은 직선이고 단면은 원형이고 솔리드인 것으로 가정됩니다. 이 요소는 독립 실행형 양식에서 사용하거나 삼각형 쉘 요소 LMT3의 한 모서리에 연결할 수 있습니다.
이 형식화는 선형 아이소파라메트릭 형상 함수를 기반으로 합니다. 전단 잠금을 방지하려면 저감 적분을 사용하여 강성 및 내부 힘을 찾습니다. 이 경우 1점 가우스 구적을 사용합니다. 결과 모델은 일정한 축, 벤딩, 비틀림 및 전단 변형 필드를 보여줍니다.
수정되지 않은 양식에서 예측된 요소 반응은 요소에 적용된 벤딩 모드에 따라 달라집니다.
단순 벤딩의 경우 제어 통합 점에서 정확한 절점 변위 및 응력 결과를 얻을 수 있습니다.
그러나 후자의 경우 페널티 이완 방법[19]을 적용하여 초과 강성을 완전히 제거합니다. 일정한 늘이기 및 비틀기에 대해서도 정확한 변위 및 중심 응력 결과가 예측됩니다.
요소 정의:
요소에 대한 지오메트리, 절점 번호 매기기 및 지역/전역 자유도는 BEAM2 빔 요소에 표시되어 있습니다. 절점 i, j는 해석 출력 파일에 제공된 절점 연결성 테이블의 항목을 나타냅니다. 예를 들어 요소의 연결성이 55, 77이면 i = 55, j = 77이고 지역 X축은 절점 55에서 절점 77까지 이어집니다.
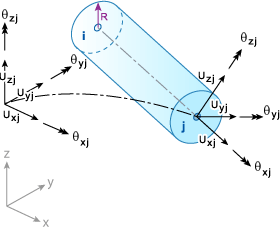
BEAM2 빔 요소
요소 하중: 현재 사용할 수 있는 유일한 요소 하중 유형은 수축으로 인한 축 및 곡률 변형의 사양입니다. 그러나 집중된 외부 하중, 즉 힘과 모멘트는 유한 요소 메쉬의 절점에 직접 적용할 수 있습니다.
- 통합 규칙
-
내부 힘(응력 결과)은 BEAM2 요소의 통합 측점에 표시된 중심 통합 점에서 계산되고 해석 출력 파일에서 재현됩니다.
선형 탄성 재료의 경우 변형 및 응력이 빔의 단면에서 선형으로 달라집니다. 따라서 비용이 더 많이 드는 수치 통합 대신 단면에 대한 명시적 사전 통합이 사용됩니다.
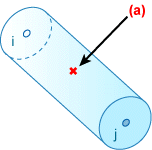
BEAM2 요소의 통합 측점
.(a) 통합 점.
- 결과 출력
-
다음 응력 결과는 통합 측점에서 계산되고 해석 출력 파일에서 재현됩니다.
모멘트: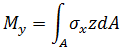
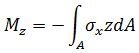 비틀림:
비틀림: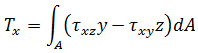 힘:
힘: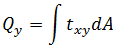
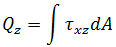
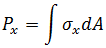
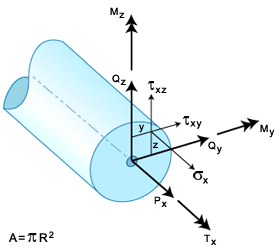
BEAM2 요소에 대한 해석 결과
모든 점(y,z)에서의 응력은 다음과 같이 지정됩니다.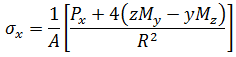
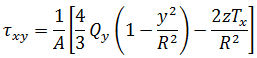
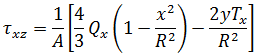
참조 문헌
- Argyris, J.H., "An excursion into large rotations", Comp. Meth. Appl. Mech. Engrg., Vol. 32, 1982, pp. 85-155.
- Rankin, C.C. and Brogan, F.A., "An element independent corotational procedure for the treatment of large rotations", in: Collapse Analysis of Structures (L.H. Sobel and K. Thomas eds.), ASME, New York, 1984, pp. 85-100.
- Bates, D.N., The mechanics of thin walled structures with special reference to finite rotations, Ph.D. Thesis, University of London, 1987.
- Hodges, D.H., "Finite rotation and non-linear beam kinematics", Vertica, Vol. 11, No. 1/2, 1987, pp. 297-307.
- Reissner, E., "The effect of transverse shear deformation on the bending of elastic plates", J. Appl. Mech., ASME, Vol. 12, 1945, A69-A72.
- Mindlin, R.D., "Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates", J. Appl. Mech., ASME, Vol. 18, 1951, pp. 31-38.
- Zienkiewicz, O.C., Taylor, R.L., and Too, J.M., "Reduced integration technique in general analysis of plates and shells", Int. J. Num. Meth. Engrg., Vol. 3, 1971, pp. 275-290.
- Fried, I., "Residual energy balancing technique in the generation of plate bending finite elements", Comp. and Struct., Vol. 4, 1974, pp. 771-778.
- McNeal, R.H., "A simple quadrilateral shell element", Comp. and Struct., Vol. 8, 1978, pp. 175-183.
- Tessler, A. and Hughes, T.J.R., "A three-node Mindlin plate element with improved transverse shear", Comp. Meth. Appl. Mech. Engrg., Vol. 50, 1985, pp. 71-101.
- Reissner, E., "On one-dimensional large-displacement finite-strain beam theory", Stud. Appl. Math., Vol. 52, 1973, pp. 87-95.
- Reissner, E., "Linear and non-linear theories of shells, in: Thin Shell Structures" (Y.C. Fung and E.E. Sechler, eds.), Prentice-Hall, Englewood Cliffs, New Jersey, 1974, pp. 29-44.
- Simmonds, J.G. and Danielson, D.A., "Non-linear shell theory with finite rotation and stress-function vectors", J. Appl. Mech., ASME, Vol. 39, 1972, pp. 1085-1090.
- Danielson, D.A. and Hodges, D.H., "Non-linear beam kinematics by decomposition of the rotation tensor", J. Appl. Mech.,ASME, Vol. 54, 1987, pp. 258-262.
- Simo, J.C. and Vu-Quoc, L., "A three-dimensional finite strain rod model. Part II: Computational aspects", Comp. Meth.Appl. Mech. Engrg., Vol. 58, 1986, pp. 79-116.
- Bergan, P.G. and Nygård, M.K., "Finite elements with increased freedom in choosing shape functions", Int. J. Num. Meth. Engrg., Vol. 20, 1984, pp. 643-664.
- Bergan, P.G. and Felippa, C.A., "A triangular membrane element with rotational degrees of freedom", Comp. Meth. Appl. Mech. Engrg., Vol. 50, pp. 25-60.
- Nygård, M.K., The free formulation for non-linear finite elements with applications to shells, Report No. 86-2, Division of Structural Mechanics, The Norwegian Institute of Technology, Trondheim, 1986.