Ta sekcja zawiera listę problemów z weryfikacją w przypadku Generatora kształtów. Jeśli to możliwe, jest ważne porównanie Generatora kształtów ze znanymi lub teoretycznymi rozwiązaniami, aby zrozumieć, w jakich sytuacjach sprawdza się on niezawodnie. Dostępne w programie Inventor 2016 R2 dla klientów korzystających z subskrypcji.
Sześcian rozciągany
W tym problemie do górnej powierzchni sześcianu jest stosowane obciążenie rozciągające. Cztery narożniki dolnej powierzchni sześcianu są ograniczone w kierunku działania obciążenia, ale mogą swobodnie przesuwać się w płaszczyźnie.
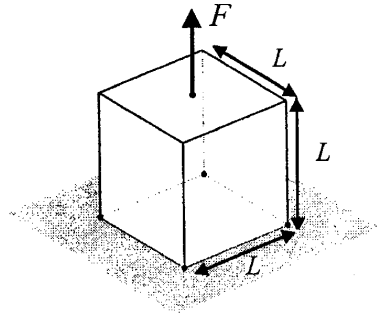

Za pomocą Generatora kształtów jesteśmy w stanie otrzymać oczekiwany wynik. Należy zwrócić uwagę, że przy przesuwanych warunkach granicznych na dole sześcianu znajdują się poziome belki, co jest zgodne z opublikowanymi wynikami [1].

Jeśli teraz zmienimy warunki graniczne, tak aby wszystkie przemieszczenia były zablokowane w czterech narożnikach na dolnej powierzchni sześcianu (jednorodny warunek Dirichleta). Oczekujemy kształtu tylko z czterema elementami diagonalnymi [1].

Belka wspornikowa
W tym problemie belka wspornikowa (L = 40, H = 25, W = 1) jest obciążana przez obciążeniem punktowym zastosowanym na wolnym końcu belki. Obciążenie punktowe jest zastosowane w połowie odległości od wolnego końca belki. Belka jest wykonana z izotropowego materiału z modułem Younga 106 i współczynnikiem Poissona 0,25.
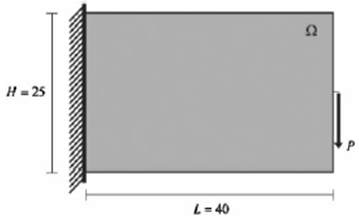
Opublikowane poniżej wyniki pokazują optymalną geometrię belki z 50% oryginalnej objętości projektu dla różnych minimalnych dopuszczalnych średnic elementów [2].
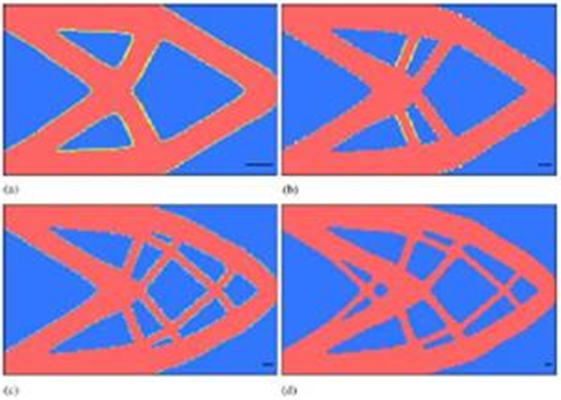
Za pomocą Generatora kształtów można uzyskać bardzo podobne wyniki w przypadku (b), gdzie minimalna średnica elementu = 2. Generator kształtów nie wymusza obecnie minimalnej wielkości elementu. Aby utworzyć część z cienkimi elementami, należy użyć wyższej rozdzielczości siatki, jak pokazano poniżej.
Jedyną zauważalną różnicą w wyniku działania Generatora kształtów jest materiał pozostały na przymocowanym (lewym) końcu belki. W tym miejscu zastosowano warunek graniczny, dlatego materiał wzdłuż powierzchni został automatycznie zachowany. Powierzchnie z zastosowanymi obciążeniami i wiązaniami są automatycznie zachowywane w Generatorze kształtów.

Most
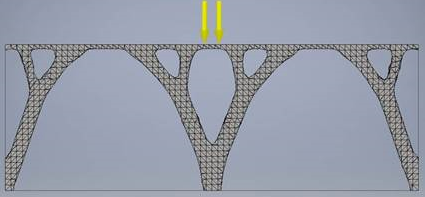
W tym problemie celem jest określenie konstrukcji potrzebnej do podparcia równomiernie rozłożonego obciążenia działającego na powierzchnię. Jak pokazano na ilustracji poniżej, istnieją trzy wiązania nieruchome na dole konstrukcji [1].
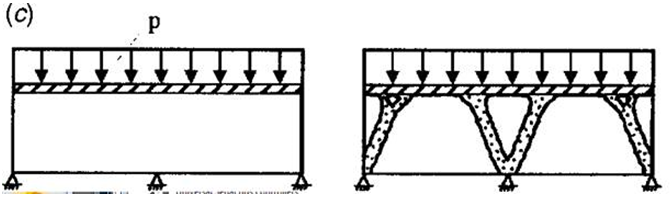
Za pomocą Generatora kształtów modelujemy tę konstrukcję jako belkę z równomiernie rozłożonym obciążeniem zastosowanym do górnej powierzchni. Trzy wiązania nieruchome są stosowane u dołu belki, po jednym na każdym końcu i jedno w środku. Wynik poniżej odpowiada w dużym stopniu opublikowanemu rozwiązaniu. Wygenerowany kształt ma postać mostu opartego na dwóch łukach, które przenoszą obciążenie ściskające na wiązania nieruchome.
Półkulista skorupa
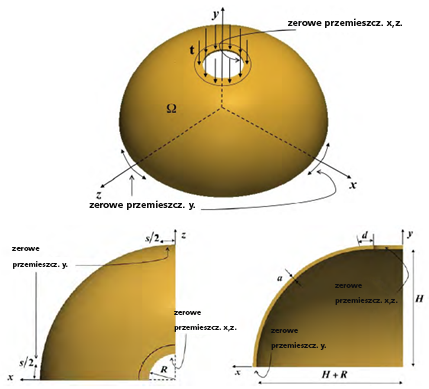
Ten problem polega na analizie cienkiej, półkulistej skorupy. Skorupa ma otwór na górze, wokół którego zastosowane jest obciążenie naciskiem. Przemieszczenia w osi y są zablokowane na dolnej krawędzi półkuli. Przemieszczenia w osi x i z są zablokowane wokół otworu w górnej części półkuli [3].
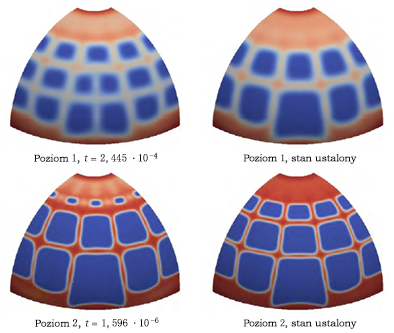

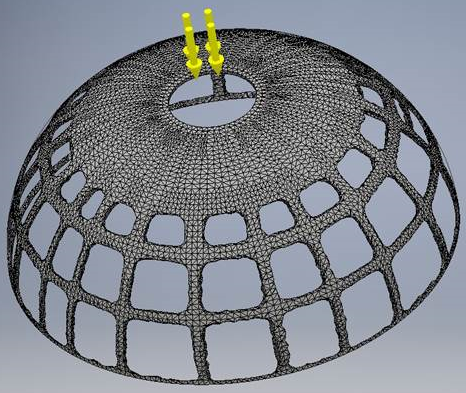
Za pomocą Generatora kształtów jesteśmy w stanie odtworzyć opublikowany wynik. Mimo iż znaczna część wyników zgadza się z opublikowanymi, na dolnej krawędzi półkuli występują pewne istotne różnice. W wyniku uzyskanym w Generatorze kształtów pozostaje tylko cienka warstwa materiału w miejscu, gdzie stosowane są warunki graniczne. Opublikowane wyniki wskazują znacznie szersze pasmo materiału wokół dolnej krawędzi półkuli. Opublikowane wyniki również wskazują pewne różnice w grubości pasma materiału, prawdopodobnie w wyniku zastosowania symetrii warunków obwiedni.
Odniesienia
- H. A. Eschenauer i N. Olhoff (2001) „Topology Optimization of Continuum Structures”, Journal of Applied Mechanics Reviews. 54(4): 372.
- J. K. Guest, J. H. Prevost i T. Belytschko (2004) „Achieving Minimum Length Scale in Topology Optimization Using Nodal Design Variables and Projection Functions”, International Journal for Numerical Methods in Engineering. 61(2): 238–254.
- L. Dede, M. J. Borden i T. J. R. Hughes (2012) „Isogeometric Analysis for Topology Optimization with a Phase Field Model”, Archives of Computational Methods in Engineering. 19(3): 427–465.