Принятые обозначения:
E - Модуль Юнга
G - модуль сдвига
ν - коэффициент Пуассона
fd - предел упругости
Ax - площадь поперечного сечения
Ix - коэффициент кручения
Iy - момент инерции - изгиб в плоскости XZ
Iz - момент инерции - изгиб в плоскости YZ
ky, kz — поправочные коэффициенты жесткости при сдвиге в направлениях Y и Z
L - длина стержня.
-
Предварительные замечания и допущения
Для стержневых (балочных) элементов были приняты следующие допущения:
- Единый способ задания для 2D и 3D (2D и 3D рамы, балочные клетки)
- Стандартный элемент допускающий нелинейность материала и/или геометрическую нелинейность
- Степени свободы при нормативном перемещении в 2 крайних узлах
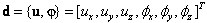
- Разрешается использовать следующее:
- Деформацию сдвига (модель Тимошенко).
- Конусное поперечное сечение: только для геометрической нелинейности.
- Основание Винклера.
- Доступны два уровня расчета геометрической нелинейности: P-дельта (теория второго порядка) и Большие значения перемещений — уровень, который представляет собой наиболее точную теорию для больших перемещений и вращений; это инкрементальный подход с корректировкой геометрии.
- При условии небольших перемещений и отсутствии физической нелинейности для предельного значения, результаты являются такими же, как для стандартных линейных элементов.
- При расчете материальной нелинейности, на уровне точки (уровня) применяются уровневая модель и конструктивный принцип "растяжение-сжатие" для одноосного растяжения-сжатия.
- Состояния сдвига и кручения рассматриваются как линейно-упругие и на уровне поперечного сечения они должны изучаться независимо от осевых сил и изгибающих моментов.
- Нелинейные снятия связей и шарниры могут быть определены только как неоднородные элементы.
- Допустимы все типы нагрузок элемента (так же, как для стандартных элементов). Однако, предполагается, что узловые нагрузки, воздействующие на конструкцию, определены в начале процесса. Изменения при переносе нагрузок элемента на узлы, проистекающие из геометрической нелинейности или нелинейности материала, не учитываются.
- Кроме упруго-пластичного элемента, также можно создать упруго-пластичные шарниры в выбранных поперечных сечениях стержня, для чего используется опция "нелинейные шарниры" (см. пункт 5).
-
Геометрия, кинематика и аппроксимация деформаций
Геометрия, правило знаков для сил, перемещений, напряжений и деформаций
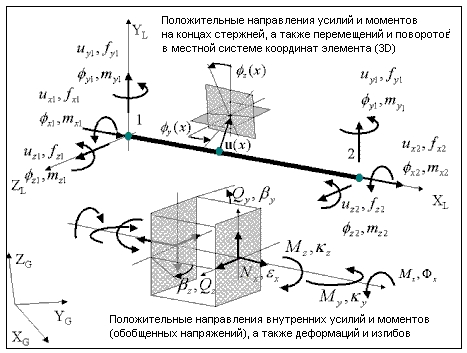
Основные кинематические соотношения
В локальной системе элементов и в геометрически-линейном диапазоне, обобщенные деформации E на уровне поперечного сечения, являются следующими (символ (
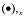указывает на вычисление дифференциала по оси стержня):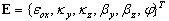 
где:
Осевая деформация (в оси стержня):
e0x = u, x
Изменения кривизны:
K y = fy'x
K z = - f z'x
Средняя величина углов (деформация):
b y = n 'x - f z'
b y = w 'x - f y
Единичный угол закручивания:
j = f x'x
Аппроксимация перемещений
Для случаев с возможностью учета влияния сдвига и при непротиворечивости результатов, полученных для линейного элемента, разработаны функции физической формы, учитывающие влияние сдвига.
2D-стержни:
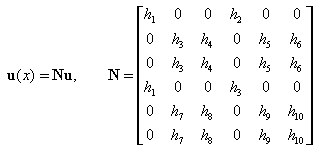
Функции формы и их производные выражены с помощью формул:
где:
x = x / L
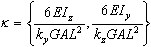для плоскостей XY и XZ, соответственно. Кинематические соотношения в матричном представлении (геометрически-линейная теория)
При рассмотрении влияния вынужденных деформаций
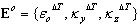
Инкремент обобщенных (в сечении) деформаций:
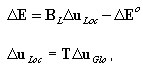
2D:
3D:
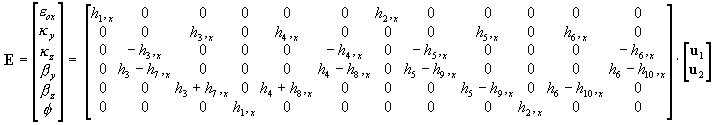
где:
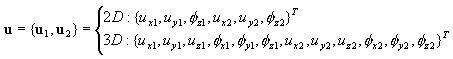
Деформации в точке (уровне)
Если обобщенные деформации {ε 0x, k y , k x }относятся к поперечному сечению, то e xl деформация или ее инкремент De xl в любой точке поперечного сечения l - координат yl, zl, вычисляется как
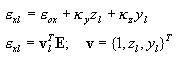
окончательно, инкремент деформации на уровне:
-
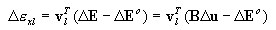
Напряжения и внутренние силы в элементе
Определяющее правило для уровня точки
Правило принято в общей инкрементной форме, в которой текущие напряжения σx n+1 определяются как функция напряжения в состоянии предельного равновесия σx n и где учтен текущий инкремент деформации с вынужденными (термическими) деформациями,
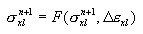
с помощью функции σ = F (ε), которая описывает соотношение в процессе активного нагружения и с помощью формулирования принципа снятия нагружения и повторного нагружения. В частности, это может быть упруго-пластический закон с линейным упрочнением, и определенный принцип снятия нагружения, такой как (а) упругий, (b) пластический, (c) с повреждениями, (d) смешанный. При упругом снятии нагружения, пассивный и активный процесс выполняется вдоль одной и той же линии σ = f(ε). Для остальных, он выполняется вдоль прямой линии, определяемой начальной точкой данного процесса снятия нагружения {ε UNL, σ UNL }и модулем снятия нагружения D UNL , задаваемым как
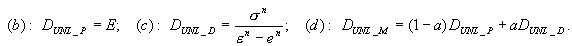
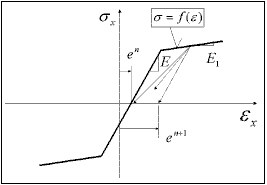
e n — запоминаемая деформация, при которой был начат текущий активный процесс, начавшийся после превышения напряжением отметки 0 с принятым снятием нагружения (е 1 = 0).
Для расчета необходимо предоставить текущую жесткость, принятую как производную
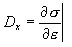
Расчет сил и значения жесткости поперечного сечения.
В поперечном сечении, вектор внутренних сил (главные векторы напряжений) состоит из:
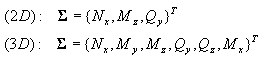
Состояния среза и кручения ΣST рассматриваются как линейно-упругие и не сопряженные с состоянием осевых/изгибающий сил в поперечном сечении.
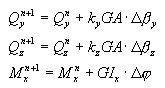
При применении многоуровневого подхода, состояния растяжения/сжатия Σ NM обычно рассматриваются как сопряженные. Однако, до тех пор, пока гарантировано эластичное состояние, то есть, пока текущие обобщенные деформации выполняют следующее условие упругого состояния:
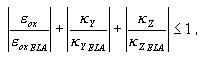
где:
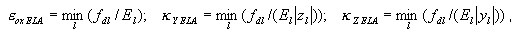
поперечное сечение рассматривается как упругое и многоуровневый подход не используется.
Как только произошло нарушение условия упругого состояния, напряжения, вызываемые осевыми деформациями и изгибами, рассчитываются отдельно для каждого уровня, и, основываясь на них, просчитываются значения для сегмента.
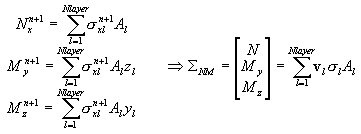
Жесткость поперечного сечения D вычисляется следующим образом:
в упругом состоянии как:
D = diag {EA, EIy, EIz, KyGA, kzGA, GIx)
После нарушения условия упругого состояния:
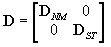
где:
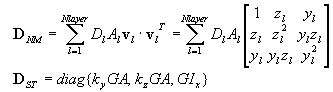
Вектор узловых сил и матрица жесткости элемента
Они рассчитываются с помощью стандартных формул, с использованием квадратуры Гаусса (Ngauss=3).
-
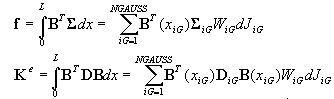
Геометрическая нелинейность
Рассматриваются следующие конфигурации:
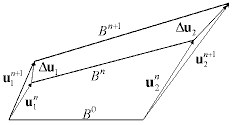
B0 - начальная конфигурация
Bn — отсчетная конфигурация (последняя, для которой выполняются условия равновесия)
Bn + 1 — текущая конфигурация (итерационная).
Исходным для формулировки элемента является принцип виртуальной работы, записанный в следующей форме для приращений перемещений:
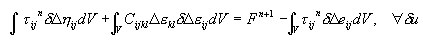
где: Δε инкремент деформации при переходе Bn к Bn + 1, Δe, Δη составляют соответственно: линейные и нелинейные части приращения перемещения Δu, тогда как τ является напряжением, относящимся к отсчетной конфигурации, и Cijkl является тензором модулей касательной упругости.
Параметр "Нелинейность"
Она соответствует формулировке нелинейности, или теории второго порядка. Так как возможна нелинейность материала, инкрементальная формулировка уже введена (однако, без учета изменения геометрии элемента).
Кинематические соотношения
Приращения деформации в матричном представлении:
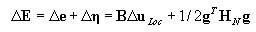
где:
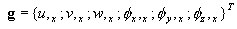
при этом градиент инкремента перемещения g = ΓΔu
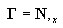
поскольку
является выбранной матрицей
Вектор узловых сил и матрица жесткости элемента
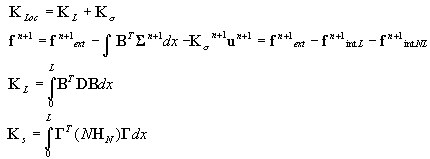
Алгоритм на уровне элемента
Геометрия элемента не изменяется; локально-глобальное преобразование выполняется с использованием начальной матрицы преобразования 0 T
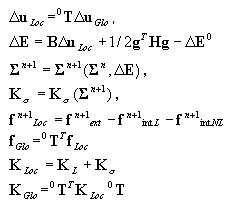
Параметр "Большие значения перемещений"
Это вариант описания стержня, используемый для больших перемещений. Здесь применяется усовершенствованный метод Лагранжа.
Вектор узловых сил и матрица жесткости элемента
-
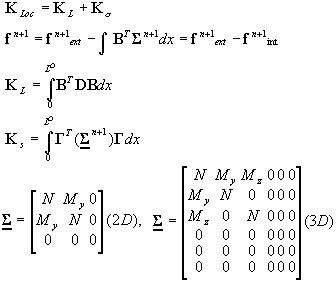
Упруго-пластические шарниры
Как вариант, упруго-пластическая работа конструкции может быть смоделирована путем введения нелинейных шарниров в выбранные поперечные сечения стержня. Характеристики шарнира, представленные 2-узловым DSC элементом, определяются при помощи алгоритма расчета поперечного сечения, описанного в пункте 3, допуская, что роль обобщенных деформаций Е играют взаимные перемещения узлов (по отношению к локальным направлениям стержня), разделенные на принятую (воображаемую) длину элемента (ΔL), которая равна минимальной высоте поперечного сечения. Они действуют как объем элемента dV=ΔL. Силы и перемещения только что созданных узлов элемента DSC, составляют глобальные степени свободы, другими словами, они не испытывают уменьшения объема.
Алгоритм на уровне элемента-
расчет обобщенных деформаций в поперечном сечении
-
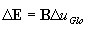
расчет внутренних сил (главных векторов напряжения) и жесткости поперечного сечения в соответствии с пунктом 3.2
-
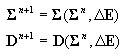
расчет сил (воздействие на концы стержня) и жесткости неоднородного (DSC) элемента
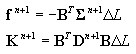
где:
-
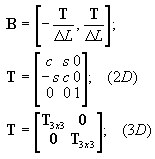