Метод нелинейного расчета состоит в пошаговом приложении нагрузок. При расчете нагрузки не учитываются одновременно, а приращиваются постепенно, а затем выполняются расчеты состояний равновесия.
Нелинейное поведение конструкции может быть обусловлено одним элементом простой конструкции (конструктивная или материальная нелинейность) или нелинейным отношением сил-деформаций во всей конструкции (геометрическая нелинейность).
К конструктивной нелинейности могут привести следующие нелинейные элементы:
- сжатые и растянутые элементы;
- вантовые элементы;
- нелинейные связи (т. е. односторонние связи или опоры, снятие связей, совместимые узлы с назначенными жесткими параметрами);
- пластичность материала;
- нелинейные шарниры.
Параметры геометрической нелинейности
Параметры геометрической нелинейности позволяют учитывать настоящие эффекты высшего порядка и часто улучшают сходимость расчетного процесса для конструкции, включающей нелинейные элементы.
- Расчет P-дельта
- Этот тип расчета учитывает второстепенные эффекты, такие как изменяющаяся жесткость элемента, находящегося под влиянием напряженного состояния элемента. Также он учитывает создание моментов, обусловленное действием вертикальных сил в узлах, смещенных горизонтально.
- Расчет больших перемещений
- В расчете этого типа учитываются эффекты третьего порядка, например, дополнительная поперечная жесткость и напряжения, вызванные деформацией или вращением. Этот эффект учитывает увеличение дополнительных сил в деформированной конструкции (например, в балке с закрепленными опорами на двух концах, нагруженной вертикальной нагрузкой, продольные силы возрастают, а прогибы уменьшаются).
Эти параметры расчета позволяют улучшить сходимость процесса расчета, поскольку они учитывают настоящие эффекты высшего порядка. Это особенно удобно при работе с конструкциями, содержащими нелинейные элементы.
Для решения системы нелинейных уравнений можно использовать два метода: инкрементальный метод и метод длины дуги.
Инкрементальный метод
Если конструкция включает нелинейные элементы (например, ванты, односторонние опоры, материальную пластичность), автоматически выполняются расчеты с применением инкрементального метода.
В инкрементальном методе правый вектор (вектор нагрузки) делится на "n" равных частей, называемых "приращения". Последовательные приращения нагрузки прикладываются к конструкции после достижения состояния равновесия для предыдущего приращения. Норма для неуравновешенных сил указывается для каждого шага, что позволяет регулировать отношения сил и деформаций.
На следующем рисунке показан пример нелинейного процесса с использованием процесса приращения. Здесь показаны величины, используемые для нелинейных расчетов.
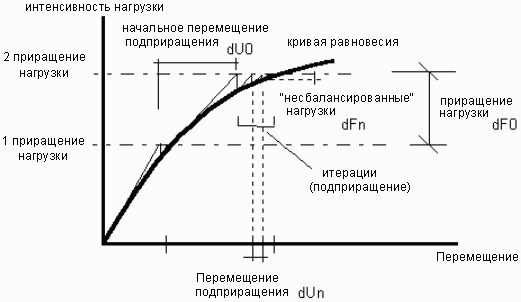
Приращения нагрузки используются при ее делении на более мелкие сегменты. У сложных конструкций, где значительно воздействие нелинейных факторов, расчеты могут не сойтись для нагрузок, приложенных единовременно. Количество приращений нагрузки влияет на количество итераций расчета. Чем больше количество приращений, тем выше вероятность того, что расчеты достигнут точки сходимости.
Метод длины дуги
Метод длины дуги (управления смещением) следует применять, когда алгоритмы решения уравнений метода приращений (управление силой) не сходятся.
Метод длины дуги применяется при нелинейном расчете на опрокидывание. Он особенно рекомендуется, когда нелинейные атрибуты конструкции определяются в ее модели (см. также приложение к руководству пользователя).
Процесс расчета
- Метод начального напряжения.
- Измененный метод Ньютона-Рафсона.
- Полный метод Ньютона-Рафсона.
Как правило, метод начального напряжения является самым быстрым, а полный метод Ньютона-Рафсона — самым медленным. Однако, вероятность сходимости с использованием полного метода Ньютона-Рафсона выше по сравнению с использованием метода начального напряжения.
В следующей таблице показано, как установить параметры изменения матрицы для использования подходящего алгоритма.
| Алгоритм | Изменение матрицы после каждого деления | Изменение матрицы после каждой итерации |
|---|---|---|
| Начальное напряжение | Выкл | Выкл |
| Измененный метод Ньютона-Рафсона | Вкл | Выкл |
| Полный метод Ньютона-Рафсона | Вкл | Вкл |
Также можно использовать процедуру модификации BFGS (Broyden-Fletcher-Goldforb-Shanno). Алгоритм метода BFGS изменяет матрицу жесткости во время расчетах. Использование алгоритма "поиск линии" может в некоторых случаях улучшить сходимость метода.
При достижении состояния равновесия итерационный процесс останавливается и проверяется сходимость процесса. Приращения смещений dUn и неуравновешенные силы dFn принимаются равными нулю или слишком малы по сравнению с допустимыми параметрами для обеих величин. Итерационный процесс останавливается, если обнаружено расхождение. Отсутствие сходимости может быть объяснено числовым эффектом перегрузки конструкции, или может являться результатом нестабильности числового процесса (например, когда нагрузка делится на небольшое количество интервалов). В таком случае количество приращений нагрузки может быть увеличено, что обычно помогает процессу сойтись.
См. также:
Элементы стержней в нелинейном расчете, доступные в программе Robot.