Алгоритм расчета деформаций железобетонных плит основан на теории упругой изотропной плиты из упругого материала, для которых учитываются изменения жесткости материала из-за образования трещин. Изначально перемещения рассчитываются методом конечных элементов (МКЭ), затем их изменяют.
Расчеты проводят отдельно для каждой плиты. Такое допущение является корректным, если плиту можно идентифицировать с конструктивным элементом (пролет, участок пола), иначе будут искажены средние значения жесткости внутри плиты. Это может привести к влиянию весьма отдаленных элементов на перемещения КЭ. Влияние таких нарушений на предельные значения не очень значительно, однако карты деформаций (прогибов) должны быть тщательно проработаны.
Рекомендуется моделировать как отдельную плиту каждый участок этажа где могут произойти локальный экстремум прогибов. Эта плита должна быть определена в пределах установленных вокруг нее опор (подобно пролетам балок, которые ограничены опорами). Для плиты эти опоры не должны быть непрерывными через весь ее контур.
Деление плиты не влияет на результаты проверки с помощью (МКЭ) с методом обновления жесткости, в том случае если нагрузки, геометрия и расчетная арматура не изменяются.
Расчет проводится для выбранного сочетания (отдельно для нижнего и верхнего перемещения) или группы сочетаний, если этого требуют нормы (частых, редких и квазипостоянных сочетаний). Это сочетание выбирается для расчета, для которого имеются максимальные упругие перемещения (отдельно положительные и отрицательные). Если плита обрабатывается не как конструктивный элемент, то карты деформаций (прогибов) должны обрабатываться весьма тщательно. Хотя это, тем не менее, особо не влияет на значения предельного прогиба отдельно взятой плиты.
Следует обратить внимание на перемещения остальных опорных точек плиты.
Алгоритм расчета в программе Robot снован на предположении, что общие (реальные) прогибы железобетонной плиты равны произведению его упругих деформаций и коэффициента жесткости D / B.
где:
- Реальное перемещение i-ой расчетной точки плиты, которые учитывает образование трещин и расчетное армирование
- Упругие перемещения i-ой расчетной точки плиты
D – Эквивалентная жесткость железобетонной плиты, предполагающая упругость материала (как в расчетах МКЭ)
B - Эквивалентная жесткость железобетонной пластины, рассчитанные с учетом трещиностойкости элемента, реологических эффектов, принятому расчетному армированию и др. и усредненная для обоих направлений.
На практике такой подход сводится к линейному масштабированию отдельных упругих деформаций с помощью глобального коэффициента приведения жесткости.
Алгоритм расчета для эквивалентной жесткости (упругим) методом представляет собой следующее:
После проведения расчета конструкции по МКЭ и расчета площади теоретической армутры по предельному состоянию 1-ой группы, в программе будет проведена оценка сооружения по предельному состоянию 2-ой группы (расчет на трещиностойкость, предельные напряжения и т. д., т. е. местные проблемы) и по особому предельному состоянию, проверка жесткости для каждого конечного элемента (КЭ). Расчет жесткости проводится для двух направлений армирования. Область и методы расчета этих значений жесткости зависят от требований отдельных норм. Результатом этого расчета являются два значения жесткости (различные по двум направлениям) полученные для каждого конечного элемента. Для дальнейших расчетов используется средневзвешенная составляющая жесткости.
где:
Bx, By – фактические значения жесткости для двух направлений армирования
cf – весовой коэффициент рассчитанный согласно формулы.
- Если | Mxx | / | Myy | > 4, то cf = 1
- Если 0.25 ≤ | Mxx | / | Myy | ≤ 4, то
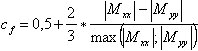
- Если | Mxx | / | Myy | < 0.25, то cf = 0.
В результате применения этих этих формул, в случае большой диспропорции моментов (отношение большего момента к меньшему больше или равно 4.0, например, плиты, изогнутые в одной плоскости), учитывается жесткость от направления действия большего из моментов. Когда величины моментов схожи, то толщина в данных направлениях назначается пропорционально отношению моментов.
Следующим этапом расчета является является оценка отношения упругой жесткости к средней взвешенной величин реальной жесткости, полученной вышеуказанным способом. Такой расчет выполняется для каждого конечного элемента.
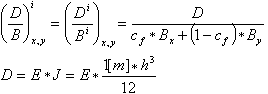
Коэффициент плиты (1 - n*n) учитывается в обоих расчетах жесткостей B и D.
Фактические значения жесткостей, получаемых при расчете, могут быть просмотрены при их подсветке на картах Коэфициент жесткости.
Если свойства материалов, используемых при проектировании, идентичны использованным в модели, тогда значение коэффициента D / B > 1.0. Этот коэффициент может быть понят (для плит, подверженных одностороннему изгибу) как множитель упругого прогиба. Если в модели и при расчете используются разные материалы (например, различный класс бетона – бетоны с разными коэффициентами Пуассона и модулями Юнга), то значение коэффициента автоматически корректируется. Это может привести к нарушению неравенства, о котором упоминалось ранее.
Следующий шаг состоит в усреднении коэффициентов жесткости, полученных ранее. Окончательный общий коэффициент жесткости, который будет использован при расчете фактических перемещений плиты (например, нанесение линейного мастаба упругих перемещений) – это число, полученное в результате усреднения средних коэффициентов жесткости (весом, равным 0.25) и коэффициента жесткости, записанного для элемента, в котором находится предельное значение изгибающего момента, действующего в любом направлении (весом, равным 0.75) по формуле:
Алгоритм метода эквивалентной жесткости (упругости) предполагает усреднение жесткости для всех конечных элементов; поэтому очертание кривой деформации идентично линии деформации умноженной на коэффициент жесткости.
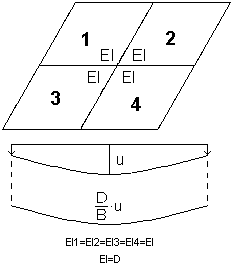
Алгоритм метода с обновлением жесткости (неупругий) идентичен алгоритму эквивалентной жесткость (упругому) до тех пор, пока вычисленная жесткость записывается отдельно для каждого конечного элемента (различные жесткости для оси X и Y). Получаем плиту с различными значениями жесткости. Для определенных таким образом значений жесткости рассчитывается прогиб плиты.
В методе с обновлением жесткости, жесткость каждого элемента вычисляется независимо друг от друга, поэтому линий прогиба, могут отличаться. Различная жесткость определяется для каждого конечных элементов для каждого направления.
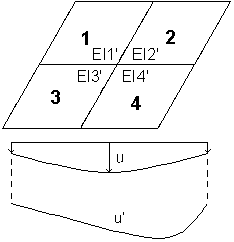
Если в процессе расчета включена опция Корректировка армирования на вкладке "Параметры" ПС2 диалогового окна "Параметры армирования" плиты и оболочки, программа увеличит площадь армирования (для увеличения жесткости элемента), что приведет к уменьшению прогиба плиты.
Армирование в двух направлениях обратно пропорционально жесткости плиты в этих направлениях. В случае, когда невозможно ограничить деформации ниже допустимой величины деформаций, определенной пользователем (дальнейшая корректировка арматуры по допустимому коэффициенту армирования невозможна), то после завершения расчетов площади теоретической арматуры, появляется следующее предупреждение, что допустимая величина деформаций для панели была превышена .
Программа не накладывает ограничений на величину коэффициента армирования иначе чем в нормативах. Поэтому следует обращать внимание на экономический аспект полученного решения, а также чем больше прогиб отличается от нормативного, тем менее эффективно использование метода.