Вантовые конструкции — это конструкции, в которых основным несущим элементом является гибкая нить в виде ванта, троса, каната и т. д. Один из размеров гибкого элемента больше, чем два других, а жесткость поперечного сечения на изгиб и кручение мала по сравнению с жесткостью на растяжение.
Соотношение осевой жесткости и длины гибкого элемента таковы, что гибкий элемент может работать только на растяжение и не воспринимает сжимающих нагрузок. Однако в некоторых случаях к такому элементу можно приложить и небольшой изгибающий или крутящий момент и поперечную силу. Наиболее ярким преимуществом гибких конструкций является то, что их гибкие элементы имеют высокие допустимые растягивающие напряжения.
Таким образом, можно использовать сечение вант для проектирования света, экономических и эстетических конструкций. Два главных фактора определяют преимущества элементов вантовых конструкций:
- во-первых, возможность создания начального натяжения, которое позволяет регулировать внутреннее усилие в элементе и делает его использование более эффективным,
- во-вторых, простота сборки (как подвесок, так и целых конструкций благодаря их небольшому весу).
Теория вантовых систем основана на следующих допущениях:
- нагрузки и другие внешние воздействия предполагаются квазистатическими и постоянными во времени;
- изгибающие моменты и поперечные силы полагаются отсутствующими и не рассматриваются;
- вантовые элементы предполагаются работающими в упруго-линейной зоне (E = const);
- к конструкции могут быть приложены любые нагрузки, кроме моментных нагрузок;
- допустимы большие перемещения u, производные перемещений полагаются малыми;
- поперечное сечение вантового элемента постоянно (F=const);
- длина не нагруженного вантового элемента обозначена как l.
Основные уравнения задачи
Рассмотрим гибкую ванту с малой величиной провисания (ванта, в которой угол между касательной в некоторой точке и прямой, соединяющей ее концы, мал) с произвольной нагрузкой, действующей в ее плоскости. Рассмотрим бесконечно малый элемент гибкой ванты, подверженный действию нагрузки q0, температуры T0 и натяжению H0. Пусть при этом длина элемента нити равна dso (рис. 1a). Когда к гибкой ванте приложена нагрузка (второй, окончательный этап нагружения с нагрузкой q, температурой T и натяжением H), длина элемента гибкой ванты становится равной ds (рис. 1b). Оба шага вместе с нагрузками в обеих плоскостях (xy и xz) представлены на рис. 2.
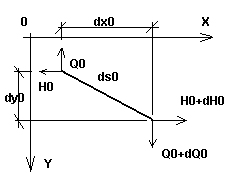 Рис. 1a |
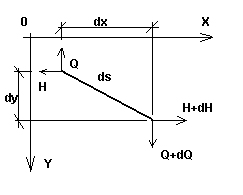 Рис. 1b |
Полагая малой величину провисания ванты и принимая во внимание, что результирующая сила натяжения должна быть касательной к оси ванты, можно допустить представление удлинения в виде функции только статических параметров. Если проинтегрировать удлинение по всей длине ванты, то будет получена известная формула для ванты с малой величиной провисания. Величина D (удлинение хорды гибкой ванты) может быть получена из (1).
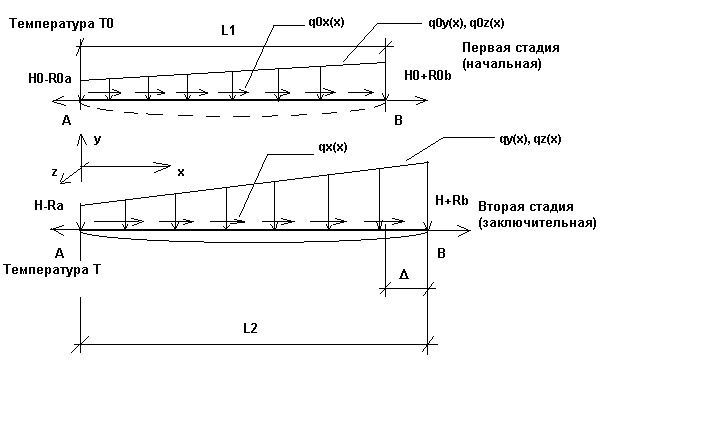
Рис. 2
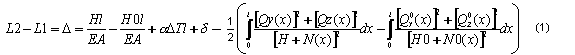
где
A, B — начальный и конечный узлы ванты;
EF — жесткость ванты на растяжение (E — модуль Юнга, F — величина поперечного сечения ванты);
a — коэффициент температурного расширения;
l — начальная длина ванты (длина не нагруженной ванты);
D — изменение расстояния между опорами;
d — начальная деформация ванты — укорочение/удлинение (регулирование);
DT — изменение температуры;
Q(x) — функция поперечной силы, вычисляемая как для балки с заделанными концами в направлениях осей Y и Z в соответствии с индексами начального и конечного узлов; эта функция схематически показана ниже (рис.
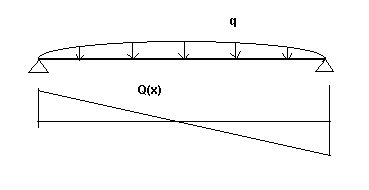
Рис. 3a
N(x) — осевая сила, вызванная статической нагрузкой при нагружении балки с фиксированными опорами (на начальном и конечном этапах) , схематически представлена на рис.
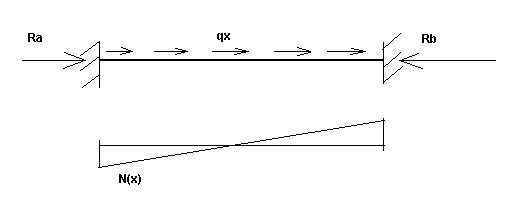
Рис. 3b
Заметим, что в уравнении каната (1), которое используется при расчете в противоположность традиционным решениям, продольная сила может изменяться по длине каната: в знаменателе обоих выражений, стоящих под знаком интеграла в уравнении (1), имеются следующие выражения: [H+N(x)] 2 and [H0+N0(x)] 2 . Это позволяет получить более точные результаты.
См. также: