Метод блочной итерации подпространства

Метод блочной итерации подпространства используется для решения обобщенной задачи на собственное значение.

Модальный расчет конструкции и анализ устойчивости конструкции обычно сводится к решению обобщенной задачи на собственное значение.

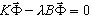
Обобщенная задача на собственное значение (1)

где:

• K — матрица жесткости;
• B = M — матрица масс для динамического варианта расчета; в остальных случаях B = Ks, где Ks — матрица "напряжение-жесткость", которая берет начало в придании линейности соответствующему нелинейному оператору при выборе расчета продольного изгиба;
• λ — собственное значение;
• Φ — собственный вектор.

Метод блочной итерации подпространства рекомендован в случаях, когда нужно получить большое число собственных пар (собственных значений и собственных векторов) конструкции. Обычно это число превышает 10.

Прим.: Метод блочной итерации подпространства может быть применен к раздельным конструкциям.

Метод блочной итерации подпространства подходит для всех типов матриц масс, а именно — сосредоточенных с вращением или сосредоточенных без вращения. Диапазон приложений метода ограничен модальным расчетом. Использование метода Ланцоша позволяет также выполнить псевдомодальный и сейсмический расчет.

Проверка Штурма: определение пропущенных собственных значений в процессе проверки.

Если опция выключена, проверка Штурма выполняться не будет. Метод блочной итерации подпространства состоит в синхронных итерациях вектора в подпространстве заданного измерения. Каждый вектор, для которого завершен процесс сходимости итераций, удаляется из рабочего подпространства и на его место добавляется новый начальный вектор. Ортогональность векторов обеспечивается на каждом шаге итераций. Применяется следующий критерий сходимости:

( 2 )

где:

i, k - число форм и число шагов итерации, соответственно

tol - допуск, заданный в поле Допуск .

Результаты модального расчета и расчета продольного изгиба определяются с заданной точностью по следующей формуле:

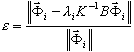( 3 )

Если процесс сходимости медленный, рекомендуется применить процедуру сдвига:

( 4 )

где:

K_σ = K - σ M,

σ - значение сдвига.

Число итераций между двумя последовательными сдвигами рассматривается как параметр этой процедуры.

Прим.: Нужно избегать установки слишком малого числа итераций между последовательными сдвигами. Это может привести частому скоплению арматуры и к декомпозиции "сдвинутой" матрицы жесткости K_σ. Это операции, требующие большой затраты времени, особенно в случае больших конструкций

Процедура сдвига не должна применяться при решении задачи устойчивости конструкции. В этой задаче существует опасность сдвига спектра собственных значений в направлении отрицательной критической нагрузки, что может привести к неучтенным положительным критическим нагрузкам, если, конечно, для данной конструкции имеются отрицательные собственные значения.

Определенные собственные пары сортируются следующим образом | λ1 | ≤ | λ 2 | ≤ ... ≤ | λ n , что приводит к тому, что минимальные параметры критической нагрузки располагаются в верхней части таблицы результатов.

См. также:

Блочная итерация подпространства – применение сдвига