结构分析中使用的单元类型（概念）

对于中性面和双层面分析技术，结构分析可同时提供薄壳单元和柱体单元。

薄壳单元

薄壳单元的形状为平面直边三角形。建立弯曲薄壳模型时，这些单元以““小面””形式来近似真实几何。当前假设每个单元的厚度为常量，尽管相邻单元的厚度可能有所不同。

任何情况下，在每个节点处使用六个位移自由度。其中包括平行于基准坐标轴的三个平移和围绕这些轴进行的三个旋转。对于平滑薄壳，可以只使用五个自由度，即三个平移和两个中间面法向的局部旋转。但在任何情况下，使用六个自由度具有明显的优势。第一，它可以分析箱子、托盘和加强壳等非平滑结构，无需向交叉面间的接合处应用任何特殊约束条件。第二，柱体单元（位于三维空间中，必须具有六个自由度）可以直接与底板或壳状网格的节点相连，无需应用约束或转换。第三，在大变形（几何非线性）分析中，使用三个旋转自由度可以为有限刚体移动引入一个几何精确的优质模型 [1-3]。值得注意的是，许多薄壁结构的现有几何非线性模型缺陷可归结于对旋转参数的逼近。这里采用的参数与相关旋转张量的光谱分析直接相关，从这种意义上讲，这些参数是“固有的”。为了获得线性化形式，Euler 和 Rodriques [1,3,4] 对刚体运动使用了经典分析。

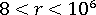
单元公式化将对膜、弯曲和横向剪切变形进行说明。后者基于 Reissner-Mindlin 理论 [5,6]。在本理论中，适用于薄板和薄壳的经典基尔霍夫假设条件有所放宽，具体是将连续性要求从 C₁ 降低至 C₀，其中包括横向剪切。这样便可为“较薄”和“厚度适中”的板和薄壳建立模型。实际上，已知这类单元的性能将随着板或薄壳变薄而迅速下降。此现象称为剪切锁定，这是由于单元无法以适当的二次方速率达到零横向剪切应变的限制条件所致。通过采用降阶积分可以缓解剪切锁定，但与早期预期 [7] 不同的是，此现象并不能消除。最近，由 Fried [8] 和 McNeal [9] 引入的能源平衡技术的变体在各种结构纵横比（围绕薄壳结构的中间面测得的特征尺寸与平均壁厚之比）范围内取得了良好成果。当前三角形单元采用的形式归功于 Tessler 和 Hughes [10]，这种形式可以在以下近似纵横比范围内获得准确结果：

除了消除锁定之外，此方法还可降低薄壳对单元变形的敏感度，改善刚度矩阵的条件约束并提高应力预测的质量。

注：膜锁定的类似问题只发生在薄弯曲单元中，所以在此无需考虑。

当前只能建立线性弹性材料的模型。这些材料可以是各向同性，也可以是各向异性。如果是各向异性，则材料的主要面相互正交，其中一个面位于薄壳的中间面上，另外两个面沿着两条垂线（称为正交方向）与该曲面相交。正交方向由工艺决定，并通过填充+保压分析对每个单元进行规定。每个方向的材料属性由用户在准备翘曲或应力分析的分析输入文件时指定。

几何非线性基于迁移拉格朗日法，在该方法中，位移场指一组随薄壳横截面在各点同步旋转的局部迁移坐标。为了保持一致，此处的常用无延伸性条件应用于在任意点与横截面方向共线的纤维上。

同步旋转法源于连续介质力学的极分解定理，该定理认为任何常规空间运动都可以始终分解为纯拉伸（变形），然后是刚体移动。采用合适的有限旋转测量（参见上文）并直接丢弃总运动的刚体分量，将获得用于求解单元中内部变形和相关应力的固定方法。实际上，这意味着不需要对刚体移动的幅度加以限制，并且求解内部变形和应力采用的精度将在整个分析中保持不变。

公式化与 Reissner [11,12]、Simmonds 和 Danielson [13]、Danielson 和 Hodges [14] 的有限变形理论以及 Bates [3] 与 Simo 和 Vu-Quoc [15] 对这些理论的有限元实现密切相关。

LMT3 单元

LMT3 单元用于中性面分析技术。LMT3 是具有 18 个自由度（每个节点上六个自由度）的三节点三角形单元。该单元的构建方法是：将 Bergan 和 Nygard [16] 及 Bergan 和 Felippa [17] 提出的局部膜公式化与 Tessler 和 Hughes [10] 提出的弯曲公式化叠加，然后将合并后的方程变换到基准坐标系。生成的单元可以建立膜和横向剪切应变的双线性变化模型，但弯曲应变（曲率）为常量。

Bergan 和 Nygard 的“无公式化”建立在假定的位移场基础上，但在允许使用“不一致”形状功能方面超出了严格的势能公式。为确保收敛，要求强制执行先验分片测试。位移形状功能分为基本模式和高阶模式，前者与刚体和恒定应变状态相关，后者则与坐标恒定的平面内弯曲模式相关。

反过来，这将导致基本和高阶刚度，分别表示为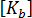

和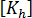

。合并的膜刚度则表示为：

其中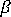是自由参数，用作高阶刚度的比例因子。根据详细的试验结果，已采用 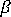= 1.5 作为最佳选择。

围绕局部中间面法向的旋转（通常称为钻孔自由度）通过罚约束技术与中间面的平均面内旋转相关联。因此，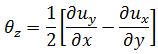

在公式化中，钻孔自由度是一个完全集成的激活组件。介于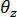和面内梯度之间的链接强度即使是在单元完全共面的情况下也保持不变，以便不再出现奇异性问题。将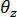用作边界条件组成时必须十分注意。

单元的弯曲公式化的基础是通过连续的横向剪切边约束 [10] 实现的显式自由度技术。这将导致总位移场受约束（耦合），侧向位移u_z 中存在二次变化，法线旋转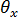和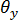中存在双线性变化。与横向剪切更正因子技术 [10] 结合使用时，单元在广大的纵横比范围内呈现显著改进的弯曲响应（与标准恒定的曲率公式化相比较）。

单元定义

单元的几何、节点编号方式和局部/整体自由度显示在 LMT3 薄壳单元中。请注意，节点 i，j，k 对应于分析输出文件中给定的节点连通性表中的条目。例如，如果某个单元的连通性为 11，101，85，则 i = 11，j = 101，k =85，局部 X 轴将从节点 11 运行到节点 101。

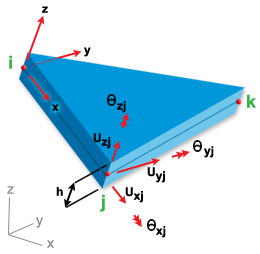
LMT3 薄壳单元

单元载荷

可使用两种类型的单元载荷：压力载荷和由于正交收缩而产生的初始应变。

假定压力载荷垂直作用在单元中间面上。假定任何给定单元上的压力都具有一个恒定值，尽管相邻单元中使用的压力值可能不同。

积分法则

使用三点数值积分法对中间面进行积分。由于材料是线性弹性材料并且单元是平的，应力和应变在整个薄壳壁中为线性变化。因此，在厚度方向上使用显式预积分而不是代价较高的数值积分。

积分位置和权重显示在 LMT3 单元的积分位置和 LMT3 单元的积分位置权重中。

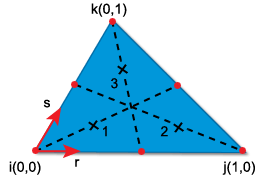
LMT3 单元的积分位置

LMT3 单元的积分位置权重
单元	积分位置	r 坐标	s 坐标
LMT3	1 2 3	1/6 2/3 1/6	1/6 1/6 2/3

结果输出

膜力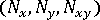、弯矩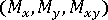和横向剪切力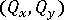将在积分位置进行计算并显示在 LMT3 单元的分析结果中。

这些结果将被复制到分析输出文件。

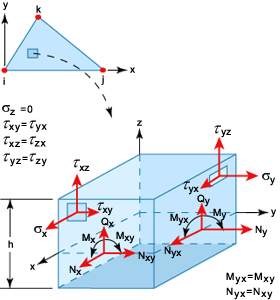
LMT3 单元的分析结果

假定任何 z 平面的平面应力状态和应力通过以下公式得出：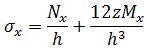

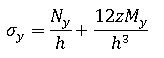
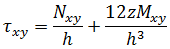
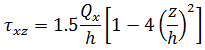请注意，所得的力和力矩是作用在一个单位宽度板或薄壳上的力和力矩，因此膜力和剪切力具有力/长度大小，而力矩具有力大小。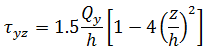

LBT3 单元

LBT3 单元用于双层面分析技术。LBT3 是具有 18 个自由度（每个节点上六个自由度）的三节点三角形单元。该单元的构建方法是：将 Bergan 和 Nygard 及 Bergan 和 Felippa 提出的局部膜公式化与 Batoz 提出的弯曲公式化叠加，然后将合并后的方程变换到基准坐标系。生成的单元可以对膜的双线性变化、弯曲应变和横向剪切应变建模。

反过来，这将导致基本和高阶刚度，分别表示为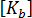

和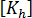

。合并的膜刚度则表示为：

其中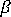是自由参数，用作高阶刚度的比例因子。根据详细的试验结果，已采用 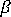= 1.5 作为最佳选择。

绕中间面法线的旋转（钻孔自由度）采用的连续介质力学定义与 LMT3 使用的连体力学定义相同，即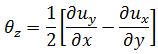

单元的弯曲公式化基于广义的离散基尔霍夫法，将横向剪切效应包括在内。单元不会锁定，适用于分析厚零件或薄零件。如果横向剪切效应不明显，它将与著名的 DKT（离散基尔霍夫三角形）单元相一致。

数值测试指示 LBT3 的效果非常好。LBT3 通常比 LMT3 略胜一筹。此外，单层和多层公式化在 LBT3 中均可用，而 LMT3 当前仅对单层分析有效。

建议使用多层 LBT3 进行纤维填充塑料的应力和翘曲分析。通过逐层考虑纤维取向，物理模型更接近现实，预期结果更加精确。

单元定义

单元的几何、节点编号方式和局部/整体自由度显示在 LBT3 薄壳单元中。请注意，节点 i，j，k 对应于分析输出文件中给定的节点连通性表中的条目。例如，如果某个单元的连通性为 11，101，85，则 i = 11，j = 101，k =85，局部 X 轴将从节点 11 运行到节点 101。

LBT3 薄壳单元

单元载荷

可使用两种类型的单元载荷：压力载荷和由于正交收缩而产生的初始应变。

假定压力载荷垂直作用在单元中间面上。假定任何给定单元上的压力都具有一个恒定值，尽管相邻单元中使用的压力值可能不同。

积分法则

积分位置和权重显示在 LBT3 单元的积分位置和 LBT3 单元的积分位置权重中。

LBT3 单元的积分位置

LBT3 单元的积分位置权重
单元	积分位置	r 坐标	s 坐标
LBT3	1 2 3	1/6 2/3 1/6	1/6 1/6 2/3

结果输出

膜力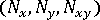、弯矩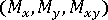和横向剪切力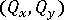将在积分位置进行计算并显示在 LBT3 单元的分析结果中。

这些结果将被复制到分析输出文件。

LBT3 单元的分析结果

假定任何 z 平面的平面应力状态和应力通过以下公式得出：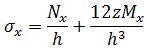

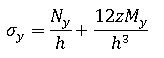
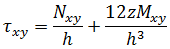
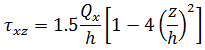
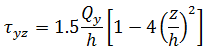
请注意，所得的力和力矩是作用在一个单位宽度板或薄壳上的力和力矩，因此膜力和剪切力具有力/长度大小，而力矩具有力大小。

柱体单元

柱体单元 BEAM2 是两节点的柱体，当前可用于中性面和双层面分析技术。

单元的纵轴是直的，因此对曲线柱体建模时，能够以“小面”形式来近似真实几何。当前，假定柱体具有恒定半径的圆形横截面。但相邻单元的横截面半径可能不同。

在每个节点处使用六个自由度，即三个自由度平行于基准轴平移，三个自由度围绕这些轴旋转。在有限旋转环境下，旋转自由度的定义与针对薄壳讨论的定义完全相同。柱体单元和薄壳单元在一个或多个节点的物理连接简单明了。请注意，如果每个柱体节点都连接到一个薄壳节点，则建模组合结构所需的方程总数与单独建模薄壳结构所需的方程总数相同。因此，增加柱体单元所涉及的计算开销通常很小。

单元公式化解释了轴向、弯曲、扭转和横向剪切变形。基本假设是柱体横截面保持为平面且无畸变，但在横向剪切存在的情况下，它将无法与纵轴保持垂直。生成的模型可认为分两个阶段来源于经典欧拉-贝努利柱体。首先，通过添加 Reissner-Mindlin 类型的剪切模型来解释横向剪切的平均效应。这通常会生成所谓的 Timoshenko 柱体。在第二阶段，使用 St.Venant 提出的理论对扭转特性进行建模。

如果使用柱体单元对流道、加强筋或独立柱体结构进行建模，则纵横比（沿柱体轴测量的总长度与平均横截面直径的比值）应处于以下近似范围内：

使用罚松弛技术可得到非常高的上限。尽管柱体单元不会受到剪切或膜锁定的影响，此技术仍可防止单元刚度矩阵在高纵横比的情况下变为病态。

目前仅能为柱体单元建立各向同性线性弹性材料的模型。请注意，在不与上述基本假设冲突的情况下，无法解释常规正交材料特性。

同步旋转法源于连续介质力学的极分解定理，该定理认为任何常规空间运动都可以始终分解为纯拉伸（变形），然后是刚体移动。采用合适的有限旋转措施并明确丢弃总运动的刚体分量，可获得用于计算单元内部变形和相关应力的一致方法。这意味着不需要对刚体移动的幅度加以限制，并且确定内部变形和应力时采用的精度将在整个分析中保持不变。

公式化与 Reissner [11]、Danielson 和 Hodges [14] 以及 Hodges 和 Simo 的有限变形理论密切相关。同时也与 Bates [1] 及 Simo 和 Vu-Quoc [15] 对这些理论的有限元实现相关。

BEAM2 单元

它是 2 节点柱体，在每个节点处有 6 个自由度。假定柱体轴是直的，横截面为圆形且实心。可以独立使用单元，也可以将单元连接到三角形薄壳单元 LMT3 的一条边。

公式化基于线性等参数形状功能。为避免剪切锁定，使用降阶积分来获得刚度和内力，在这种情况下意味着使用一点高斯求积。生成的模型将呈现恒定的轴向、弯曲、扭转和剪切应变场。

在其未修改的形式中，预测的单元响应取决于影响单元的弯曲模式。

对于纯弯曲，在控制积分点处可获得准确的节点位移和应力合力。

但是，通过应用罚松弛法 [19] 可以完全消除后一种情况中的刚度过度现象。还可以预测恒定拉伸和扭转的准确位移和集中应力合力。

单元定义：

单元的几何、节点编号方式和局部/整体自由度显示在 BEAM2 薄壳单元中。请注意，节点 i，j 对应于分析输出文件中给定的节点连通性表中的条目。例如，如果某个单元的连通性为 55，77，则 i = 55，j = 77，局部 X 轴将从节点 55 运行到节点 77。

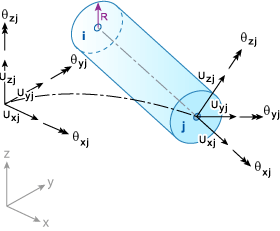
BEAM2 柱体单元

单元载荷：当前唯一可用的单元载荷类型是由于收缩而指定的轴向和曲率应变。（但请注意，集中的外部载荷（即，力和力矩）可直接施加到有限元网格的节点上）。

积分法则

内力（应力合力）在 BEAM2 单元的积分位置中显示的中央积分点处计算，并复制到分析输出文件中。

对于线性弹性材料，应力和应变在柱体的横截面上线性变化。因此，在横截面上使用显式预积分而不是代价较高的数值积分。

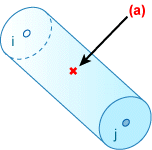
BEAM2 单元的积分位置

(a) 积分点。

结果输出

以下应力合力将在积分位置处进行计算并复制到分析输出文件中。

力矩：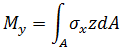

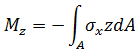扭矩：

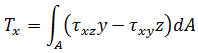力：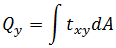

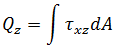
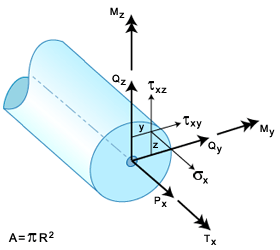
BEAM2 单元的分析结果

任意点 (y,z) 处的应力由以下等式得出：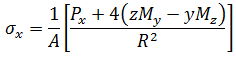

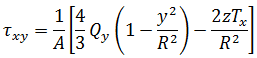
参考

Argyris, J.H., “An excursion into large rotations”, Comp. Meth. Appl. Mech. Engrg., Vol. 32, 1982, pp. 85-155.
Rankin, C.C. and Brogan, F.A., “An element independent corotational procedure for the treatment of large rotations”, in: Collapse Analysis of Structures (L.H. Sobel and K. Thomas eds.), ASME, New York, 1984, pp.85-100.
Bates, D.N., The mechanics of thin walled structures with special reference to finite rotations, Ph.D. Thesis, University of London, 1987.
Hodges, D.H., “Finite rotation and non-linear beam kinematics”, Vertica, Vol. 11, No. 1/2, 1987, pp. 297-307.
Reissner, E., “The effect of transverse shear deformation on the bending of elastic plates”, J. Appl. Mech., ASME, Vol. 12, 1945, A69-A72.
Mindlin, R.D., “Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates”, J. Appl. Mech., ASME, Vol. 18, 1951, pp. 31-38.
Zienkiewicz, O.C., Taylor, R.L., and Too, J.M., “Reduced integration technique in general analysis of plates and shells”, Int. J. Num. Meth. Engrg., Vol. 3, 1971, pp. 275-290.
Fried, I., “Residual energy balancing technique in the generation of plate bending finite elements”, Comp. and Struct., Vol. 4, 1974, pp. 771-778.
McNeal, R.H., “A simple quadrilateral shell element”, Comp. and Struct., Vol. 8, 1978, pp. 175-183.
Tessler, A. and Hughes, T.J.R., “A three-node Mindlin plate element with improved transverse shear”, Comp. Meth. Appl. Mech. Engrg., Vol. 50, 1985, pp. 71-101.
Reissner, E., “On one-dimensional large-displacement finite-strain beam theory”, Stud. Appl. Math., Vol. 52, 1973, pp. 87-95.
Reissner, E., “Linear and non-linear theories of shells, in: Thin Shell Structures” (Y.C. Fung and E.E. Sechler, eds.), Prentice-Hall, Englewood Cliffs, New Jersey, 1974, pp.29-44.
Simmonds, J.G. and Danielson, D.A., “Non-linear shell theory with finite rotation and stress-function vectors”, J. Appl. Mech., ASME, Vol. 39, 1972, pp. 1085-1090.
Danielson, D.A. and Hodges, D.H., “Non-linear beam kinematics by decomposition of the rotation tensor”, J. Appl. Mech.,ASME, Vol. 54, 1987, pp. 258-262.
Simo, J.C. and Vu-Quoc, L., “A three-dimensional finite strain rod model.Part II: Computational aspects”, Comp. Meth.Appl. Mech. Engrg., Vol. 58, 1986, pp. 79-116.
Bergan, P.G. and Nygård, M.K., “Finite elements with increased freedom in choosing shape functions”, Int. J. Num. Meth. Engrg., Vol. 20, 1984, pp. 643-664.
Bergan, P.G. and Felippa, C.A., “A triangular membrane element with rotational degrees of freedom”, Comp. Meth. Appl. Mech. Engrg., Vol. 50, pp. 25-60.
Nygård, M.K., The free formulation for non-linear finite elements with applications to shells, Report No. 86-2, Division of Structural Mechanics, The Norwegian Institute of Technology, Trondheim, 1986.