Use common functions to analyze a composite plate.
- Composite Plate
- In Helius Composite, a plate is considered to be a rectangular laminate whose thickness dimension (H) is much smaller than its width dimension (W) or length dimension (L). The image below shows the plate geometry, and the position and orientation of the plate within the global coordinate system. The thickness restriction (H<<W, H<<L) is necessary to ensure that practical methods of loading the plate result primarily in in-plane and bending deformations. In other words, the plate does not exhibit significant transverse shear deformation or transverse normal deformation (εxz≈0, εyz≈0, εzz≈0). Under these conditions, Classical Laminate Theory is appropriate for modeling the response of the plate to in-plane and bending loads, or modeling the lower natural vibration frequencies and buckling loads of the plate.
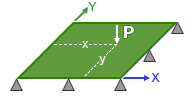
For the purposes of discussing the bending response of plates, the adjective transverse will be used to indicate the through-the-thickness direction (or global Z direction). In Helius Composite, a bending analysis of laminated plates is performed using Fourier series methodology originally developed by Navier. In this methodology, the transverse displacement component of the plate's mid-plane, w(x,y), and the distributed transverse (pressure) load p(x,y) are each expressed in terms of a double sine series as shown in the equations below [see Vinson & Sierakowski (1987), or Whitney (1987)].
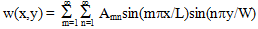
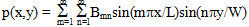
In this scheme, the coefficients Amn of the transverse displacement component are the primary unknowns sought in the solution process.
Plate Analysis
The Plate Analysis window, accessed from the Plate drop-down menu, provides access to three different laminated plate analysis features: Bending, Stability and Vibration. Below is a brief description of each of the three laminated plate analysis features accessible from the Plate Analysis window. A detailed description of these three analysis features and their use is given on the pages that follow.
- Bending - Compute the transverse deflection of a simply supported or clamped plate in response to a concentrated or uniformly distributed transverse load.
- Stability - Compute the critical buckling load of a laminated plate subjected to uniaxial in-plane compression or biaxial in-plane compression.
- Vibration - Compute the fundamental vibration frequency of a laminated plate subjected to simply supported or clamped boundary conditions.
The Plate Analysis window has five tabs. The first two are the Laminate tab and the Plate Geometry tab. Once the laminate and the plate geometry are defined, you may select from one of the three analysis tabs to conduct bending, stability, or vibration analyses. Upon selecting one of these tabs, feature-specific options will enable you to define aspects of the execution. A detailed description of these tabs is included in the sections listed below.