The MCT criterion is based on the Multicontinuum Theory39,40 (MCT). The concept of multicontinuum extends the notion of a continuum to reflect distinctly different materials that coexist within a representative volume element (RVE). Such an extension is natural in any case where there are two or more clearly identifiable constituents with drastically different material properties. Hence, a unidirectional fiber-reinforced composite material may be viewed as two interacting continua (a fiber continuum and a matrix continuum) that coexist within a suitably chosen RVE of the composite material.
In traditional continuum mechanics (as applied to fiber-reinforced composite structures), attention is focused on the development of relationships between the various composite average quantities (e.g. stress, strain). Multicontinuum Theory (or MCT) augments traditional continuum mechanics by expanding the focus to include two additional issues: 1) the development of relationships between the various constituent average quantities of interest, and 2) the development of relationships that link the composite average quantities to the constituent average quantities.
MCT predicts failure at the fiber and matrix level as opposed to the composite or lamina level. This is done by first obtaining the volume averaged stress states in the fiber and matrix. The constituent stresses are a function of the composite stress and the stiffness of the composite fiber and matrix.
The MCT Decomposition
The fiber and matrix stresses are obtained via the following stress and strain decomposition process. The first step is to obtain the strain state in the matrix:
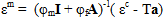
where φf and φm represent the volume fraction of the fibers and matrix respectively, I is a 6x6 identity matrix, A and a relate the average mechanical and thermal strain in the constituents respectively. They are defined as follows:
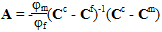
The strain in the fiber can then be found using:
Now the fiber and matrix stress states can be calculated:
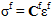
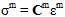
The constituent stresses are used to evaluate failure in the fiber and matrix separately.
MCT Matrix Constituent Failure Criterion
The following assumptions are employed in developing the matrix constituent failure criterion for unidirectional composites.
- Matrix failure is assumed to be influenced by all six of the matrix average stress components
, 
, 
, 
, 
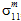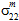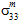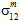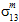, and 
. - The matrix constituent material is assumed to be transversely isotropic. Consequently, you cannot distinguish between the contributions of 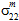and 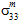to matrix failure, nor can you distinguish between the contributions of 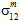and 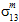to matrix failure.
- The influence of the matrix average normal stresses (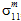, , 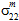and 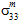) in producing matrix failure depends upon whether the normal stresses are tensile or compressive.
Using these four basic assumptions, the matrix failure criterion is expressed as a quadratic function of the matrix average stress components.
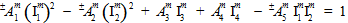
In the above equation, the quantities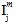 
(j=1,2,3,4) are transversely isotropic invariants of the matrix average stress state.
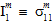
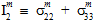
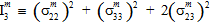
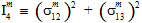
The quantities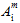 
(i=1,2,3,4,5) are the coefficients of the matrix failure criteria. If a superscript symbol '±' precedes a coefficient 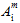, the symbol indicates that the numerical value of 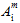depends on whether the associated matrix average stresses are tensile or compressive. Hence 
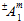represents two possible values. For the coefficient 
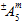, there are actually four possible values depending on whether 
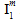is positive or negative and also depending on whether 
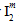is positive or negative. Therefore, the matrix failure criterion contains a total of ten adjustable coefficients that must be determined using measured strengths of the composite material.
MCT Fiber Constituent Failure Criterion
- Fiber failure is assumed to be influenced by the fiber average stress components
, 
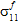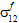, and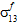 
. - Fiber failure is assumed to be independent of the fiber average stress components
, 
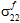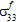, and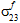 
. - The contribution of 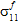in producing fiber failure depends upon whether 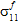is tensile or compressive.
- The fiber constituent material is assumed to be transversely isotropic. Consequently, you cannot distinguish between the contributions of 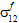and 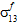to fiber failure.
Using these four basic assumptions, the fiber failure criterion is expressed as a quadratic function of the fiber average stress components.
The quantities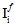 
(i=1,4) are two of the transversely isotropic invariants of the fiber average stress state.
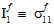
The quantities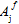 
(j=1,4) are the adjustable coefficients of the fiber failure criteria. If a superscript symbol '±' precedes the coefficient 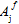, the symbol indicates that the value of 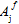depends on whether the associated fiber average stresses are tensile or compressive. Hence 
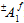represents two possible values. Therefore, the fiber failure criterion contains a total of three adjustable coefficients that must be determined using measured strengths of the composite material.