制御されたカオスの概念は、パーティクル システムの本質です。カオスを[データ](Data)オペレータに適用するには、[ランダム](Random)サブオペレータを使用します。[ランダム](Random)サブオペレータは、このセクションで説明するように、さまざまなアルゴリズムを使用してスカラー形式とベクトル形式のランダム値を生成します。
[ランダム](Random)の例
参照オブジェクトの周囲にパーティクルをカオス状態で配置する方法の例から始めます。組み込みの RandomPositioning.max を参照してください。
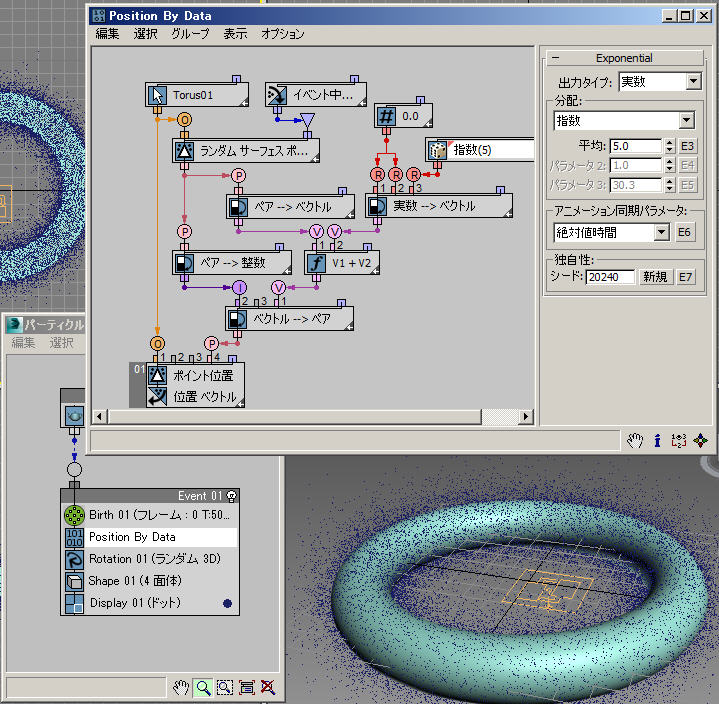
上の例のデータ フローにおいて、[ジオメトリ](Geometry)サブオペレータ(1.)は、参照オブジェクトのサーフェス上にランダムなポイントを均等に分布させます。次にそのペア データ出力は、2 つの異なる[変換](Convert)サブオペレータ(面ローカル座標(2.)およびランダムなポイントが配置される面インデックスを含んだ合成インデックス(3.))に分割されます。
参照オブジェクトを囲むパーティクルの適切な分布ボリュームを求めるため、サーフェスからパーティクルを「持ち上げる」必要があります。それには、面ローカル座標ベクトルの Z コンポーネントに変更を加えます。Z コンポーネントは、面法線方向の面からの距離です。
[ランダム](Random)サブオペレータ(4.)を使用して、「持ち上げる」量を定義できます。この例では、0 周辺で正の値になり、密度が高くなる指数分布を使用しました。したがって、サーフェスに近いほど多くのパーティクルが配置され、サーフェスからの距離に応じて徐々に密度が低くなります。
次に、変更した面ローカル座標値と合成インデックスが元のペア データ形式に変換されます。[ジオメトリ](Geometry)サブオペレータ(5.)は、この値を使用してワールド座標でのパーティクル位置を計算します。
[ランダム](Random)サブオペレータの分布パラメータについてさらに詳しく説明します。このパラメータにより、サブオペレータで使用されるランダム関数のタイプを定義します。関数のタイプは、[ランダム](Random)サブオペレータによって生成されるデータ タイプによっても異なります。
次の説明では、組み込みのシーン ファイル RandomTemplate.max を開きます。このファイルを使用して、さまざまな分布関数を再生できます。
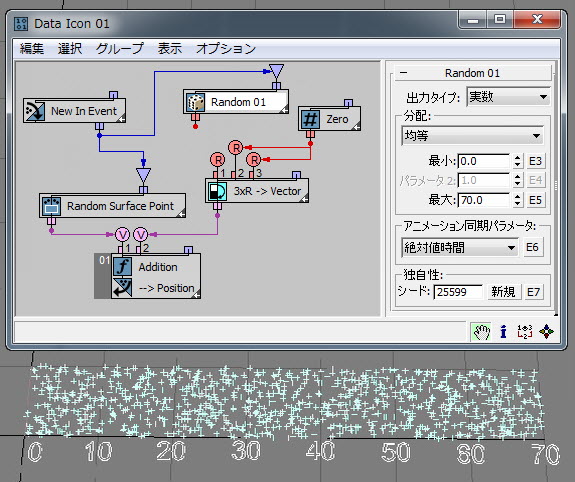
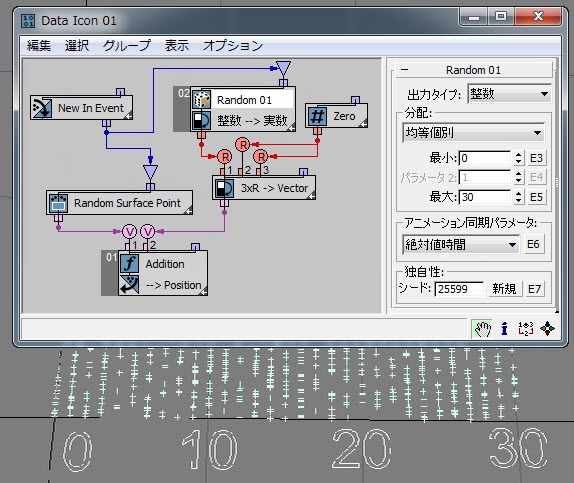
まずは、単純な分布タイプである[均等個別](Uniform Discrete)から始めます。これは、[ランダム](Random)サブオペレータを[整数](Integer)データ タイプに設定する場合に使用できる唯一のタイプです。離散は継続の反対です。[ランダム](Random)サブオペレータは、この UI で定義された[最小](Minimum)値と[最大](Maximum)値の間に均等に分布する整数データ(その意味で離散)を生成します。次の例( RandomTemplate01.max )では、[最小](Minimum)値と[最大](Maximum)値が 0 と 30 に設定されています。その結果、X 座標軸(0、1、2、3 ... から 30 まで)の線に沿ってパーティクル位置が分布していることを確認できます。均等個別分布の理論の詳細については、こちらを参照してください。
[実数](Real)データ出力タイプについては、使用可能なさまざまな分布タイプが用意されています。
[均等](Uniform)分布タイプは[均等個別](Uniform Discrete)タイプに非常によく似ていますが、分布範囲を定義するための最小値と最大値があります。ただし、出力値は範囲間隔内に連続的に分布するようになっています。均等分布の詳細については、こちらを参照してください。
[指数](Exponential)分布オプションは、一般に信頼性エンジニアリングで使用されます。これは、真にランダムな一定の障害率を示す単位の動作をモデル化する場合にも使用できます。指数分布の別の例には、放射性崩壊における不安定なパーティクルの個々の存続期間の分布があります。
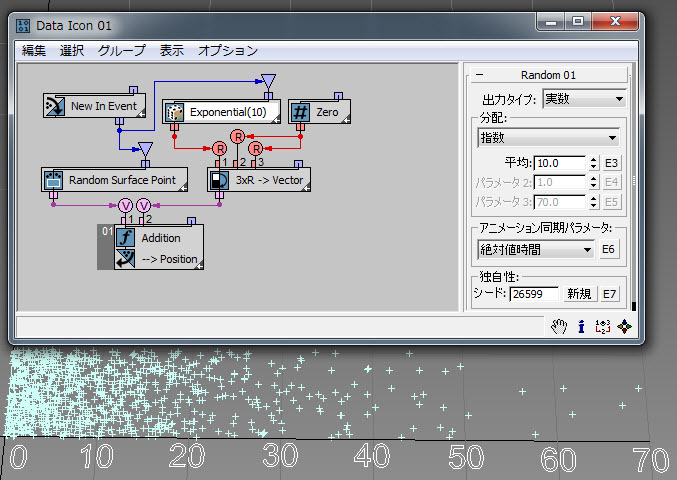
[指数](Exponential)分布オプションでは、正の値のみが生成されます。生成される値のおよそ半分は[平均](Mean)パラメータ値未満で、0 に近づくほど多くの値が生成されます。生成される値は任意の大きな値になる可能性がありますが、値が大きくなるほど生成される確率も低くなります。この例( RandomTemplate02.max )では、[平均](Mean)値が 10 になっています。そのため、生成される値のほとんどが 0 と 70 の間にあります。指数分布の詳細については、こちらを参照してください。
[法線](Normal)つまり[ガウス](Gaussian)分布オプションでは、観察の独立したランダム エラーの分布を表現します。一般に法線分布または近似法線分布となるその他の分布には、体温、靴のサイズ、木の直径などがあります。法線分布グラフは、左右対象の鐘形カーブです。[平均](Mean)パラメータにより生成される値の平均値を定義し、[シグマ](Sigma)パラメータにより生成される値が平均値から外れるときの距離の程度を定義します。値の大半(99.7%)は 3 シグマ オフセット間隔内で生成されます[平均 3 * シグマ、平均 + 3 * シグマ]。次の例( RandomTemplate03.max )では、[平均](Mean)パラメータが 30 で、[シグマ](Sigma)パラメータが 10 に設定されています。したがって、生成される値の大半は間隔[0.0、60]の範囲内に入ります。法線分布では、正負の値が生成されます。生成される値は任意の大きな値になる可能性がありますが、値が大きくなるほど生成される確率も低くなります(上の 3 シグマ ルールを参照)。法線分布の詳細については、こちらを参照してください。
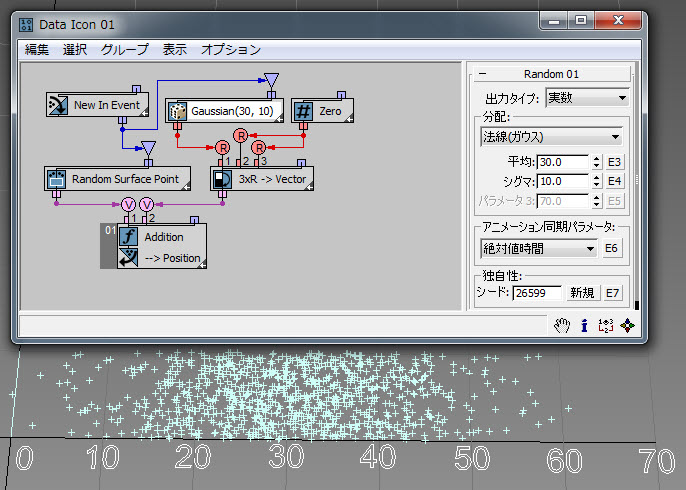
[三角](Triangular)分布オプションは、何らかの[ピーク](Peak)値を示す傾向があり、かつ[最小](Minimum)値と[最大](Maximum)値によって決まる範囲内に制限されるランダムな事象を表現するのに簡潔な方法です。この例( RandomTemplate04.max )では、三角分布によって前の例の法線分布をエミュレーションします。三角分布の詳細については、こちらを参照してください。
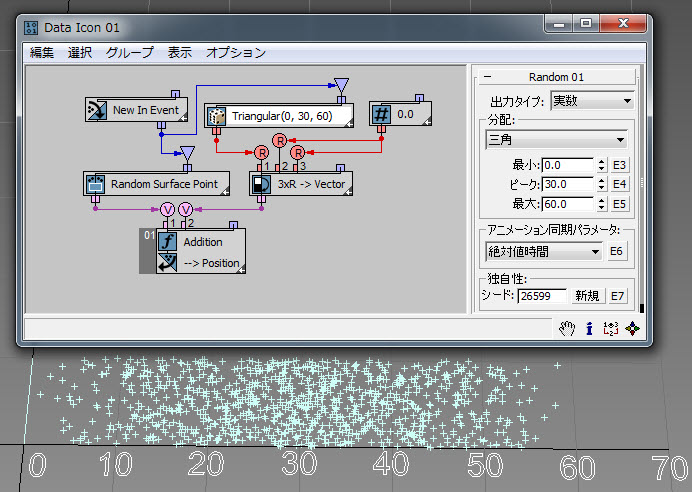
ワイブル分布法は、指数分布を純粋にランダムではないイベントにまで拡張したものです。通常この分布は、信頼性および経年に伴う存続期間のモデル化で使用されます。この例( RandomTemplate05.max )では[レート](Rate)パラメータが 1.0 と等しいため、ワイブル分布は、[平均](Mean)パラメータをワイブルの[スケール](Scale)パラメータとした場合の指数分布と等しくなります。
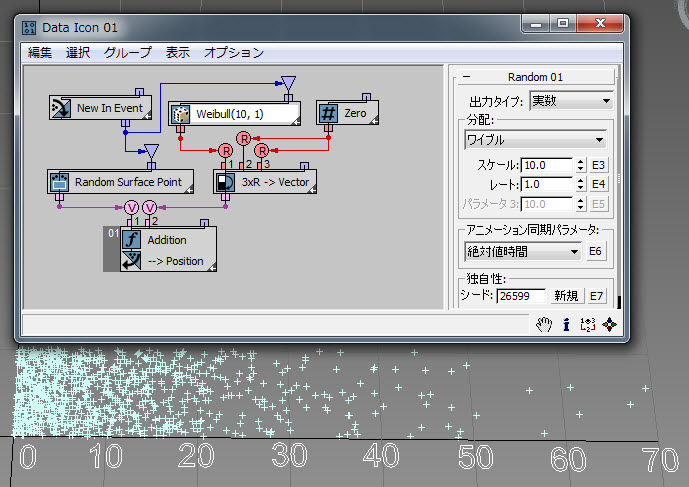
ワイブル分布を使用すると、所定の技術デバイスが故障するまでの時間をモデル化できます。デバイスの故障率が時間とともに減少する場合は、[レート](Rate)を 1 未満の値に設定します。デバイスの故障率が時間とともに上昇する場合は、[レート](Rate)を 1 超の値に設定します。ワイブル分布は、地上の指定された場所における風速の分布をモデル化する場合にも使用できます。すべての場所は、特定の[レート](Rate)および[スケール](Scale)パラメータで特徴付けられます。この例( RandomTemplate06.max )では、故障率を 4 に、[スケール](Scale)を 10 に設定して、ランダム値の大半が間隔[3.0、15.0]の範囲内に生成されるようにしています。ワイブル分布の詳細については、こちらを参照してください。
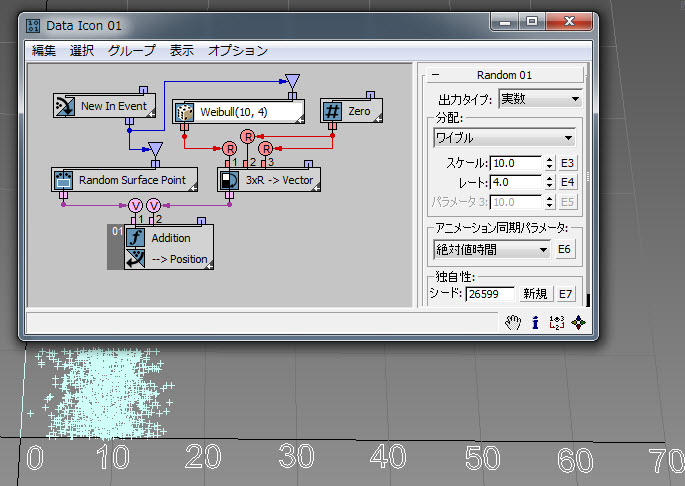
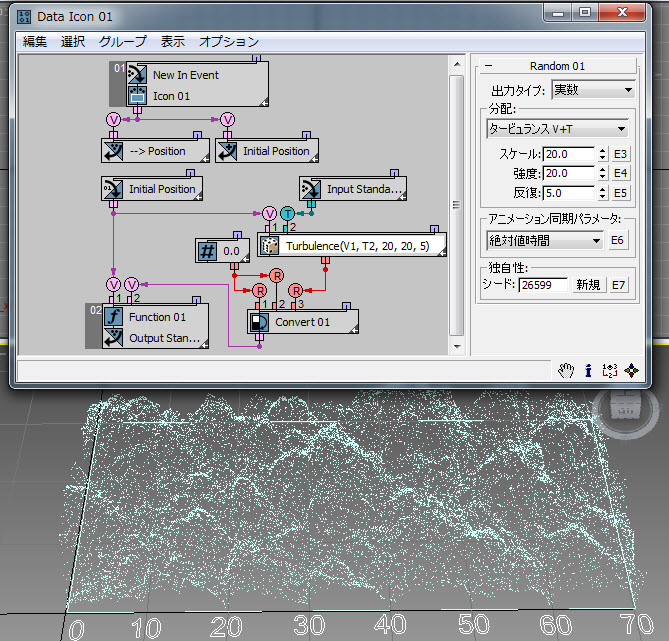
[ノイズ R](Noise R)、[ノイズ V](Noise V)、[ノイズ V+T](Noise V+T)、[タービュランス V](Turbulence V)、および[タービュランス V+T](Turbulence V+T)オプションを使用して、実数、ベクトル、または時間の入力データを基に擬似ランダム ノイズ タイプ値を生成できます。[スケール](Scale)パラメータにより、入力データと出力データの間の依存率を設定します。値が大きくなると、ノイズが滑らかになり、小さいとぎざぎざになります。[強度](Strength)パラメータにより、出力値の絶対値を制御します。
[タービュランス](Turbulence)オプションには、フラクタル ノイズの生成で使用される反復つまりオクターブの数を制御する[反復](Iterations)パラメータがあります。[反復](Iteration)値を低くするほど、スムーズな出力が作成されます。[反復](Iterations)パラメータの範囲は 1.0 ~ 10.0 です。[ノイズ](Noise)オプションでは正負の出力値が生成され、[タービュランス](Turbulence)オプションでは正の値のみが生成されます。
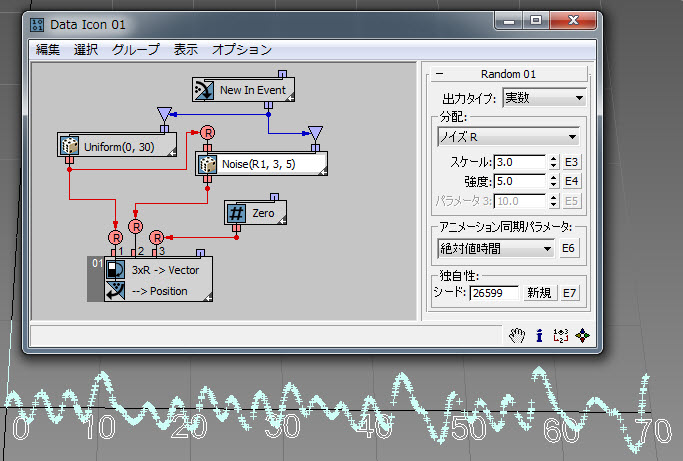
この例( RandomTemplate07.max )では、パーティクルのランダム X 座標を使用して、Y 座標のノイズに似たランダム値を生成します。
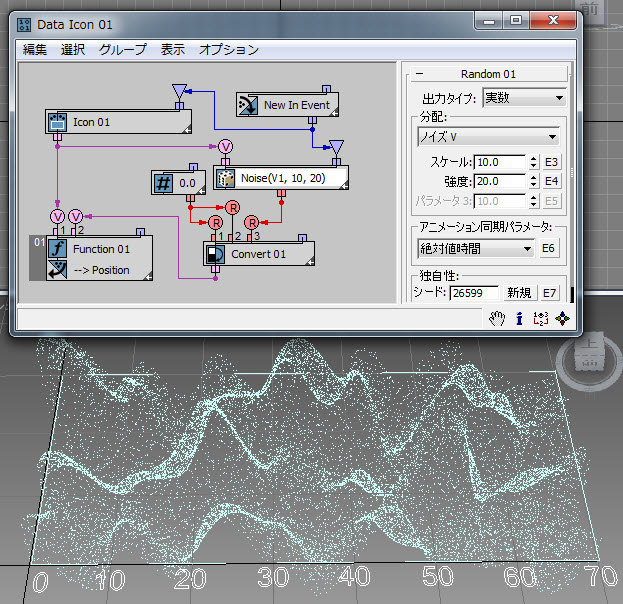
次の例( RandomTemplate08.max )では、パーティクルが[データ オペレータ](Data Operator)アイコンのサーフェスにランダムに配置され、次にその位置が、[ノイズ V](Noise V)オプションが指定されたランダム サブオペレータの入力として使用されます。出力データは、パーティクルの高さ(Z 軸位置)を定義するために使用されます。
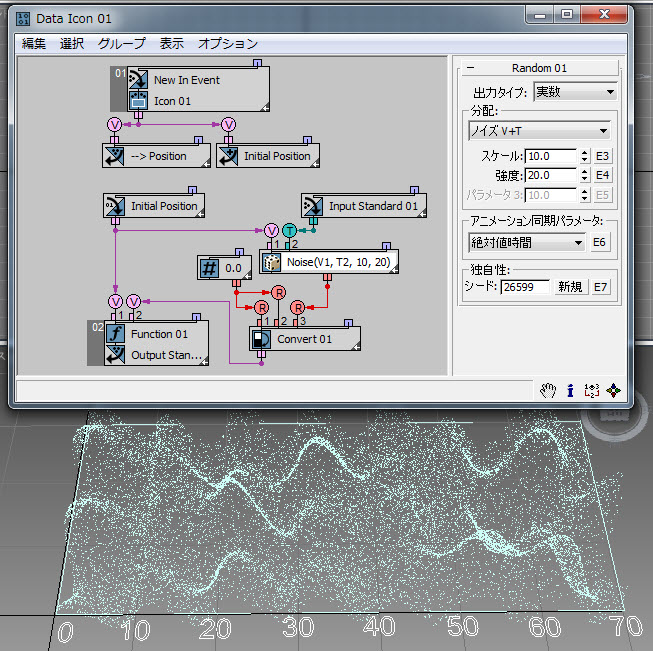
[絶対値時間](Absolute Time)を[...+T]オプションの[時間](Time)入力にワイヤリングすることにより、この例( RandomTemplate09.max )に示すように、生成されるノイズを容易にアニメートすることができます。
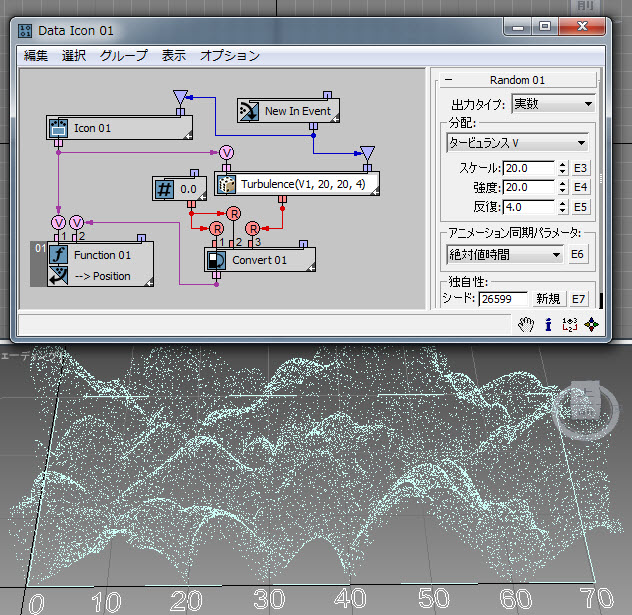
[タービュランス](Turbulence)オプションは、[ノイズ](Noise)オプションによく似ています。この例( RandomTemplate10.max )に示すように、[反復](Iterations)パラメータを定義するだけです。
次の例( RandomTemplate11.max )も同様です。
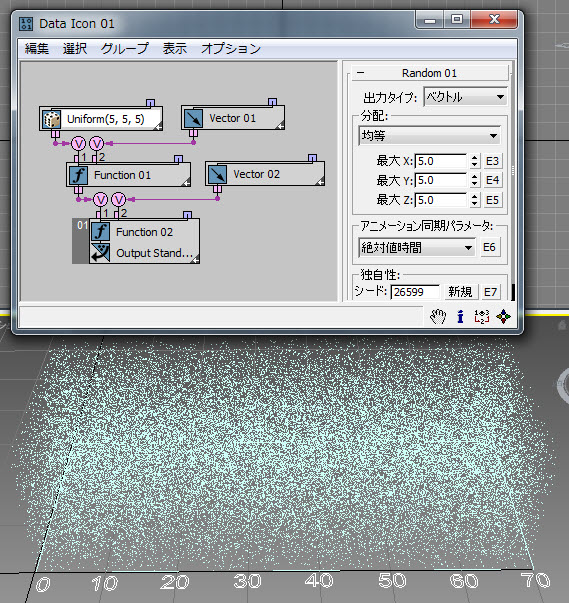
分布オプションの最後のカテゴリでは、ベクトル データを出力します。
[均等](Uniform)分布オプションでは、制限値が X コンポーネントについて[- 最大 X、最大 X]、Y コンポーネントについて[- 最大 Y、最大 Y]、および Z コンポーネントについて[- 最大 Z、最大 Z]になっているバウンディング ボックス内部に、ランダムなベクトル値が生成されます。十分な数のパーティクルにより、バウンディング ボックスをランダムなベクトル ポイントで満たすことができます( RandomTemplate12.max) 。
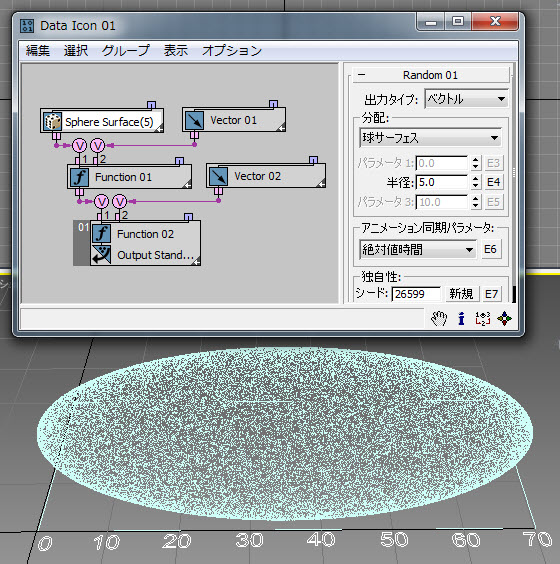
[球サーフェス](Sphere Surface)オプションを使用すると、球のサーフェスにパーティクルを配置できます。ただし、最も一般的な使用例は、ランダム方向でのベクトルの生成です。この場合は、[半径](Radius)パラメータによって、ベクトルの長さを定義します( RandomTemplate13.max): 。
または、球体積全体をランダムなポイントで満たすこともできます( RandomTemplate14.max): 。
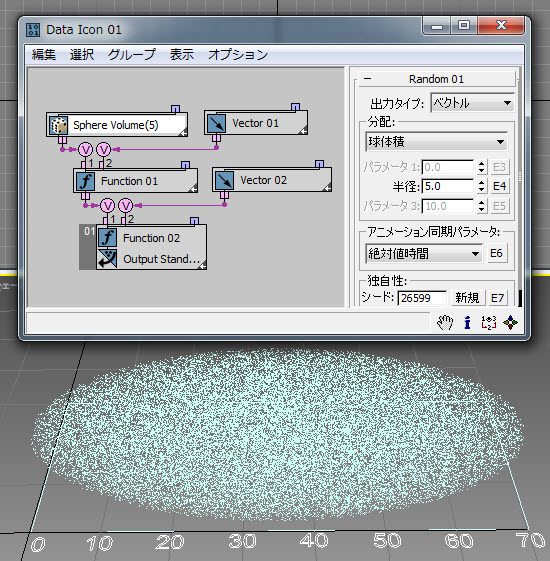
[法線](Normal)([ガウス](Gaussian))オプションを使用しても球体積を満たすことができますが、このオプションの場合は球の境界がありません。そのため、球の中心近くに多くのポイントが生成され、外側に向かって減少します。ここでも前と同じ 3 シグマ ルールを適用することができ、ポイントの 99.7% が 3 * シグマに等しい半径の球内部に生成されます( RandomTemplate15.max)。
[ノイズ V](Noise V)、[ノイズ V+T](Noise V+T)、[タービュランス V](Turbulence V)、および[タービュランス V+T](Turbulence V+T)オプションは、ベクトル データを生成することを除いて、同じ名前の[実数](Real)データ オプションに似ています。出力データを描出するには、事後ステップの[速度](Speed)チャネルにデータを差し込み、事前ステップで速度を 0 に設定します。この方法により、パーティクルをどこにも移動せずに、出力を速度線として描画できます。この例( RandomTemplate16.max) では、パーティクルが長方形内にランダムに配置され、その位置が[ノイズ V](Noise V)オプションが指定された[ランダム](Random)サブオペレータの入力として使用されます。
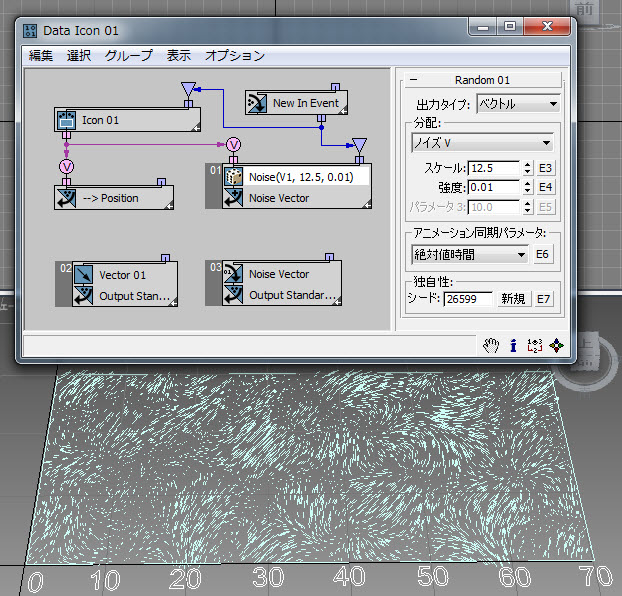
また次の例( RandomTemplate17.max) は、設定が同じで、[ノイズ V+T](Noise V+T)オプションが指定された場合です。現在時刻を[ランダム](Random)サブオペレータの入力として使用し、ノイズ出力をアニメーションにしています。
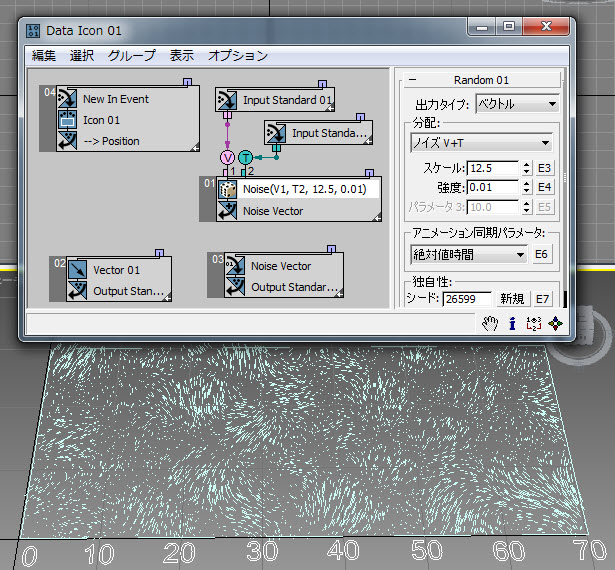
ランダム出力を[速度](Speed)チャネルにワイヤリングし、[位置](Position)チャネルを[ランダム](Random)サブオペレータの入力として使用できます。[ランダム](Random)サブオペレータを使用すると、風の乱流をシミュレーションできます。これは、シーン ファイル RandomTemplate18.max のフレーム 98 です。
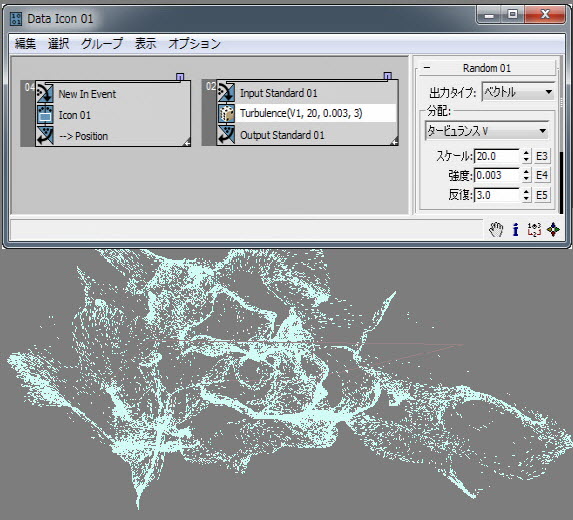
インタフェース
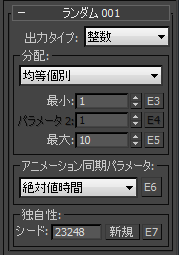
- 出力タイプ(Output Type)
- 次の中から出力するデータ タイプを選択します。
- 整数値
- 実数(Real)
- ベクトル
[出力タイプ](Output Type)の設定により、[分配](Distribution)領域で設定可能なパラメータが決まります。
[分配](Distribution)領域
[分配](Distribution)ドロップダウン リストの内容は、[出力タイプ](Output Type)での選択項目によって決まります。代わって[分配](Distribution)での選択により、[分配](Distribution)領域で設定可能な残りのパラメータが決まります。
[分配](Distribution)オプションと関連パラメータに関する特定の情報については、上の説明を参照してください。
- [アニメーション同期パラメータ](Parameters Animation Sync)
- サブオペレータ パラメータをアニメートする場合、アニメーションの開始フレームまたは現在のイベントの開始フレームからすべてのパーティクルに対してこのアニメーションの適用を開始するか、エージに基づいて各パーティクルに適用することができます。オプションは次のとおりです。
- [絶対値時間](Absolute Time) パラメータに設定された任意のキーが、設定対象の実際のフレームで適用されます。
- [イベント期間] パラメータに設定された任意のキーが、最初にイベントに入った時点のフレームに関連する各パーティクルに適用されます。
- [パーティクル エージ](Particle Age) パラメータに設定された任意のキーが、各パーティクルが存在する対応するフレームで適用されます。
- [パーティクル寿命](Particle Lifespan)パラメータのアニメーションをパーティクル寿命期間にスケール/マップします。たとえば、パラメータ値がフレーム 0 ~ 100 の 5 ~ 20 からアニメートされている場合、このパラメータの値はパーティクルが発生したときは 5 で、パーティクルの期限が切れると 20 になります。この方法により、たとえば、その寿命でのパーティクルのスケールの変更を定義できます。
このオプションを正しく使用するには、フローで[削除](Delete)オペレータを[パーティクル エイジ](By Particle Age)に設定し、パーティクル寿命を定義する必要があります。
- [時間データ入力](Time Data Input)サブオペレータに[時間](Time)入力を追加し、時間形式でデータを出力する他のサブオペレータをリンクできるようにします。
- E6
- [アニメーション同期](Animation Sync)値を制御するための等しいタイプのデータ入力を追加します。このデータ入力では、[タイプ](Type)が[アニメーション同期](Animation Sync)に設定された[パラメータ](Parameter)サブオペレータからの入力だけを受け取ることができます。
- 独自性(Uniqueness)
- [ランダム](Random)サブオペレータによって生成されるランダム数シーケンスをさまざまに変化させることができます。[シード](Seed)値を手動で入力するか、[新規](New)をクリックしてソフトウェアに[シード](Seed)値を生成させます。
- E7
- [独自性](Uniqueness)値を制御するための等しいタイプのデータ入力を追加します。このデータ入力では、[タイプ](Type)が[独自性](Uniqueness)に設定された[パラメータ](Parameter)サブオペレータからの入力だけを受け取ることができます。