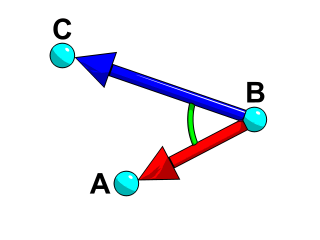
3 つの頂点間の角度を調べる方法はありますか。

質問:

面を定義する頂点が 3 つあります。面のコーナーの角度を調べる方法はありますか。

回答:

面には常に 3 つの頂点があります。頂点のペアはそれぞれ、面の 3 つのエッジのいずれか 1 つを定義すると同時に、ベクトルとみなされます。 「頂点の位置からベクトルを作成する方法はありますか。」のFAQ トピックで説明したように、すべての頂点はもともとベクトルを表し、2 つの頂点を結ぶエッジ ベクトルは、2 つの頂点の位置を差し引くことで簡単に計算できます。

3 つの頂点 A、B、および C を呼び出してみます。 頂点 A における角度を計算する場合、頂点 A から頂点 B へのベクトルと頂点 C へのベクトルが必要になります。 これら 2 つのベクトルは、次の式で表されます。

V1 = B-A

V2 = C-A

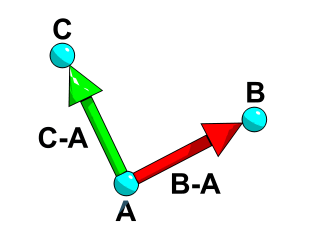
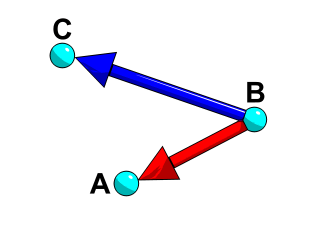
このイメージには、座標[0,0,0]の点 A 、座標[2,0,1]の点 B、および座標[-1,0,2]の点 C が示されています。

さて、2 つのベクトルが得られましたが、ベクトルの内積で有効な結果を得るには、単位ベクトルが必要になります。単位ベクトルは、元のベクトルと方向は同じですが、長さが 1.0 になります。

ベクトル V1 V2 に対して正規化メソッドを使用することによって、単位ベクトルを計算できます。

N1 = normalize V1

N2 = normalize V2

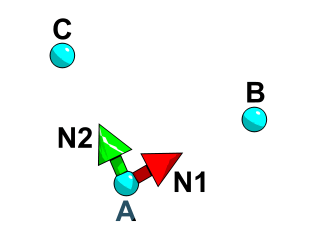
V1 = [2.0.1]の場合、N1 = normalize V1 の式は、[0.894427,0,0.447214]の値を返します。 これは、length V1 = 2.23607 であり、X、Y、Z 座標のそれぞれの値を、この長さで除算することにより計算されるためです。 つまり、 [2/2.23607, 0/2.23607, 1/2.23607]と計算されます。

N2 = normalize V2 の式は、[-0.447214,0,0.894427]の値を返します。 これは、ベクトル[-1,0,2]の長さも 2.23607 であり、単位ベクトルは [-1/2.23607, 0/2.23607, 2/2.23607]と計算されるためです。

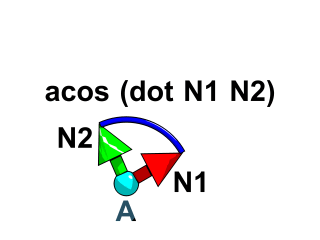
最後に、「2 つのベクトル間の角度を調べる方法はありますか。」で説明したように、これらの単位ベクトルの内積の acos (アークコサイン) を計算する必要があります。acos は cos (コサイン) の逆関数であり、cos がオペランドに等しくなる角度を返します (つまり、X = cos Alpha の場合、Alpha = acos X)。

Angle = acos (dot N1 N2)

角度の範囲は、0 度 (2 つのベクトルが平行な場合) から 180 度 (2つのベクトルが反対方向を向いている場合) までです。

上記の[0,0,0]、[2,0,1]、および[-1,0,2]の座標を使用した例では、点 A での角度は 90 度になります。

点 B での角度を計算するには、同じ手順に従いますが、ベクトル A-B とベクトル C-B を使用します。

続いてベクトルを単位化し、内積を計算して、この値の acos を求めます。この例における点 B での角度は、45 度になります。