[摩擦]タブ

このページでは、ネイティブの Simulation Mechanical (SimMech)ソルバーを使用した、非線形シミュレーション実行における一般表面間接触の摩擦パラメータについて述べます。これらのパラメータは[接触オプション]ダイアログ ボックスの[摩擦]タブにあります。 このタブは、[一般]タブの[摩擦を含む]オプションをオンにした場合にのみ表示されます。

摩擦のない接触の場合、要素剛性マトリックスは対称です。 摩擦が含められると、マトリックスは非対称になります。非対称のソルバを使用すると、通常の対称ソルバーを使用する場合よりも計算コストが高くなります。効率を考慮して、MES では強制的に要素剛性を対称とし、摩擦のある接触に対称ソルバーを使用できるようになっています。

解析で摩擦のある接触を考慮する場合、解法プロセスは、すべりのプロセスからの影響を非常に受けやすくなります。 接触サーフェスがすべりを開始すると、すべり前の平衡状態は有効でなくなり、プロセッサでは、解法プロセス中に新しい平衡状態を探す必要があります。さらに、対称の近似により、収束性に乏しい可能性があります。使用可能な摩擦則の各オプションは、ソリューションが不安定になることをさまざまな方法でコントロールしようとします。

[摩擦]タブの上部にあるドロップ ダウンメニューから、目的の[摩擦則:]を選択します。 Simulation Mechanical には、非線形の表面間接触に対して 3 つの選択肢があります。

これらの摩擦則のそれぞれとそれに適用されるパラメータは、以下のサブセクションで説明しています。

修正されたクーロン摩擦

この摩擦則は、古典的な摩擦アルゴリズム「クーロン摩擦」を使用します。基本的なクーロン摩擦モデルにおいては、2 つの接触サーフェスが所定の大きさまでのせん断応力に抵抗することができます。この大きさは、摩擦係数と、相対すべり運動を受ける前の垂線方向の接触圧から決定されます。クローン摩擦モデルは、τ = μP と定義されます。ここで、μ は摩擦係数、P は法線方向の接触圧です。修正されたクーロン摩擦則を使用した場合は、次の 3 つのパラメータを定義する必要があります。

理想状態では、静摩擦係数から得られた μsP をせん断応力が超えた後、2 つのサーフェスがすべりを開始します。さらに、せん断応力は動摩擦係数を使用した μdP になります。

理想状態(せん断応力が静的な値を超えるまで運動なし)を数値的に達成するのは、図 1 に示すように困難です。そのため、この摩擦則の使用時に[接線の剛性比率]が定義されます。接線方向の剛性比とは、法線方向の接触剛性(K)に対する、接線方向の接触剛性(Kt)の比のことです(接触剛性(K)は[高度]タブで定義されます。)このページの「高度タブ」セクションを参照してください。接線方向の剛性が大きいほど、結果の精度が向上しますが、その代償として、より多くの反復が必要になります。 接線方向の剛性が小さいほど、収束性に優れます(実行時間が短縮されます)が、精度が低下する可能性をともないます。推奨される値は、0.01～1 の範囲です。 静摩擦係数が大きくなるほど、接線方向の剛性比を小さくすることが推奨されます。

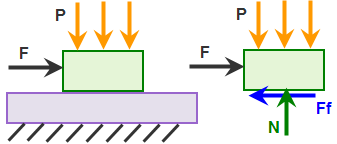
ヒント: 解析実行時間が長引く原因となる発振を防ぐには、静摩擦係数とすべりの摩擦係数が接近しないようにする必要があります。

(a) トップ ブロックのモデルと自由物体図(Free body diagram)。加えられた力 F は、静摩擦力を超えるまで、時間とともに徐々に増加します。

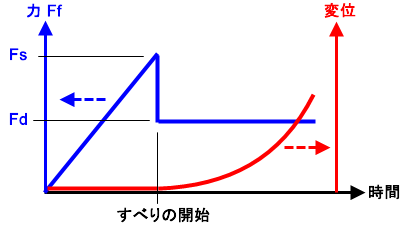
(b) 摩擦力 Ff の時間変化(青色の曲線)と変位の時間変化(赤色の曲線)。 摩擦力 Ff が静摩擦の限界(Fs = μs * N)を超えるまで、パーツの運動はありません。静摩擦を超えると、摩擦力 Ff は Fs から Fd (= μd * N) にまで低下し、パーツは加速を開始します。

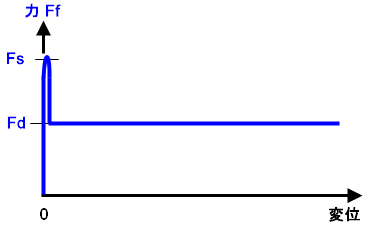
(c) (b)のグラフは摩擦力と変位の関係を示すように組み合わされています。理想状態では、摩擦力が Fs に達するまで変位はゼロであり、その後にすべりが開始します。数値上でこれを実現するのは困難です。変位がゼロでない場合はすべて摩擦力が Fd であること意味するためです。

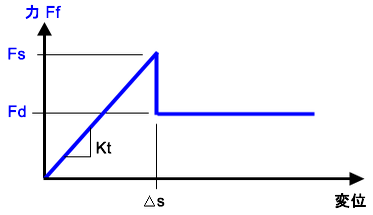
(d) (c)における数値的な不安定さを回避するために、摩擦力が静的限界(Fs)未満のときに、パーツが少し(Δs)だけ変位できるようになっています。運動の大きさは、接線方向の剛性(Kt = Fs/Δs)によってコントロールされます。Kt の値が小さいほど、パーツはすべりを開始する前に大きく変位することがで、収束が容易になります。一方、Kt の値が大きい(勾配が急である)ほど、すべりを開始する前の変位は小さくなり、収束が困難になります。 接線方向の剛性は、(接線方向の剛性比) x (垂線方向の剛性)によって計算されます。

図 1: 修正クーロン摩擦に対する接線方向の剛性

粘性摩擦のあるクーロン

修正されたクーロン摩擦則とは異なり、静摩擦および動摩擦の摩擦係数はともに粘性摩擦のあるクーロンを考慮しません。修正されたクーロン摩擦則では、静摩擦および開始モーションを解決するために、比較的高い力が必要です。スライドを開始すると、スライド摩擦係数が静止係数より小さくなっているため、摩擦力が減少します。したがって、摩擦力の急激な変化により、力の不連続が発生します。粘性摩擦のあるクーロン則では、スライドが始まっても、摩擦力の不連続は発生しません。代わりに、スライドの速度が高まると、摩擦力が徐々に増加します。

[粘性摩擦のあるクーロン]オプションでは、2 つのパラメータを定義する必要があります。

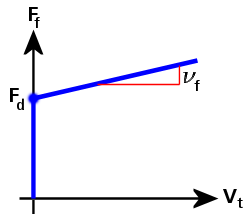
図 2: 摩擦力対スライド速度(粘性摩擦のあるクーロン)

図 2 で、摩擦力(Ff)曲線は次のように定義されます。

Ff = Fd + νf · Vt
ここで
Fd は動(スライド)摩擦力、
νf は粘性摩擦係数、
Vt は、2 つのパーツ間の接線(スライド)速度です。

νf = 0 の場合は、Ff = Fd です。

クーロン摩擦を平滑化

粘性摩擦のあるクーロン則と同様に、クーロン摩擦を平滑化則もスライド摩擦係数のみを考慮します。これよにり、修正されたクーロン摩擦則を使用した場合に発生する静止状態とスライド状態の摩擦力の連続性が中断されます。静止状態とスライド状態間の遷移が、よりスムーズな遷移係数(Φ)の包含によって安定化されます。

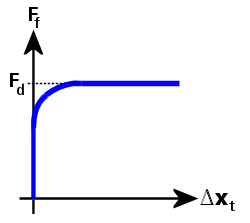
図 3: 摩擦力対接線相対変位(クーロン摩擦を平滑化)

図 3 で、摩擦力(Ff)曲線は次のように定義されます。

Ff = Fd · Φ、および
Φ = tanh(3 · Δxt / δ)
ここで
Fd は動(スライド)摩擦力です。
Φ は遷移係数であり、接線の相対変位がゼロに近づくにつれて摩擦力をスムーズにゼロへアプローチさせることができます。同様に、接線の相対変位が増えるにつれて摩擦力をスムーズに動摩擦力へアプローチさせることができます。
Δxt は接線の相対変位であり、
δ は接触剛性および動的摩擦力に基づいて計算される許容値です。
親トピック: Simulation Mechanical の表面間接触オプション(非線形)