위에 나오는 지배 PDE 각각은 앞서 설명된 유한 요소 메서드를 사용하여 이산화됩니다. 대수 방정식의 결과 세트를 해석하여 유한 요소의 노드에서 종속 변수 값을 확인해야 합니다. Autodesk® CFD에서 이러한 방정식의 해를 구하는 데 사용하는 알고리즘은 이 섹션에 설명되어 있습니다.
분리형 솔버
불연속화 방정식의 해를 구할 때 해결해야 할 첫 번째 문제는 압력이 누락되는 문제입니다. 속도 구성요소를 계산하는 데 운동량 방정식을 사용하는 경우 연속 방정식을 사용하여 압력을 결정해야 합니다. 그러나 연속 방정식에는 압력이 명시적으로 나타나지 않습니다. 암시적 압력 커플링의 수치적 어려움을 피할 수 있는 여러 가지 방법이 있습니다. 이러한 풀이 방법 대부분에서는 유한 요소 메쉬의 모든 노드에 대해 연속 방정식 및 운동량 방정식의 해를 동시에 구해야 합니다. 작은 문제의 경우 이 솔루션이 매우 적합합니다. 그러나 대부분의 실제 문제에서, 이 솔루션을 구하는 데 컴퓨터 리소스가 상당히 많이 사용되며, 실제로 솔루션을 구하지 못할 수 있습니다. 이러한 제한을 해결하기 위해 압력이 명시적으로 지정되는 방정식을 찾아야 합니다.
Autodesk® CFD에서 해를 구하는 압력 방정식은 연속 방정식에서 파생됩니다. 연속 방정식의 가중 적분은 적분 순서를 줄이기 위해 부분별로 적분이 사용되는 경우에 계산됩니다.
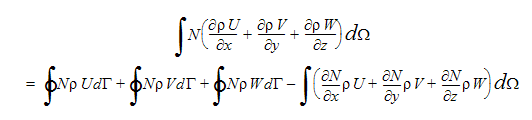
이 방정식의 오른쪽(RHS)에 나오는 처음 3개의 정수는 요소 경계 간의 질량 플럭스를 나타냅니다. 이러한 정수는 내부 요소 면에서 취소되고, 질량 유량(대칭, 벽)이 없는 모든 경계에서 0이 됩니다. 이러한 항은 압력 방정식의 자연 경계 조건을 나타냅니다.
이 방정식에서 압력의 모양을 강제로 적용하려면 속도와 압력 간 관계가 파생되어야 합니다. 이 관계는 운동량 방정식에서 추론할 수 있습니다. 반분리화 양식의 운동량 방정식을 사용하면 속도-압력 관계를 다음과 같이 작성할 수 있습니다.
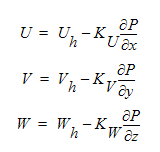
이러한 방정식에서 Uh, Vh, Wh 항에는 운동량 방정식의 모든 비대각 항이 포함됩니다. 이러한 세 개의 방정식이 이제 이전 연속 방정식으로 대체되면 다음과 같은 압력 방정식 결과가 얻어집니다.
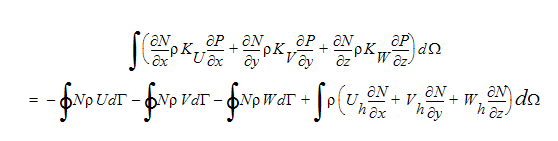
이 방정식은 불연속 양식의 푸아송 방정식이므로 대칭 계수 행렬을 생성합니다.
압축성 흐름에서는 밀도-압력 커플링도 고려해야 합니다. 이 커플링은 다음 표현식을 사용하여 계산됩니다.
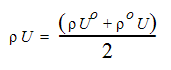
여기서 o는 이전 값을 나타냅니다. 이 표현식은 연속 방정식이 부분별로 적분될 때 사용됩니다. 그런 다음 속도롤 대체하면 다음 결과가 생성됩니다.
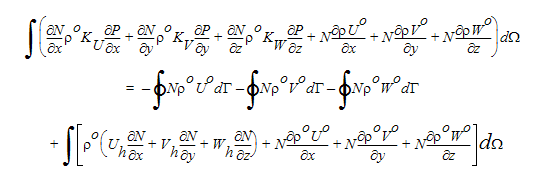
이 방정식 왼쪽의 추가적인 유사 이류 항은 이상 기체 법칙을 사용하여 압력 측면에서 다시 작성됩니다. 이러한 추가적인 이류 항을 사용할 경우 압축성 압력 방정식은 다른 전달 방정식처럼 비대칭 계수 행렬을 생성합니다.
명시적인 압력 방정식을 사용할 경우 각 지배 방정식의 해를 따로 구할 수 있습니다. 즉, 모든 노드의 U에 대해 x-운동량 방정식을 구할 수 있고, 모든 노드의 V에 대해 y-운동량 방정식을 구할 수 있고, 모든 노드의 W에 대해 z-운동량 방정식을 구할 수 있으며, 모든 노드의 P에 대해 압력 방정식을 구할 수 있습니다. 한 번에 자유도 하나만 해석되므로 훨씬 더 적은 양의 메모리로도 충분합니다. 이 접근 방법은 각 종속 변수가 별도로 계산되므로 분리형 솔버 라고 합니다. 또한 이러한 각 방정식은 반복 행렬 기법으로 해를 구할 수 있으므로 계수 행렬의 0이 아닌 행만 저장하면 됩니다.