多点约束

注： 本部分中的信息适用于线性结构分析、热分析和静电分析。

多点约束 (MPC) 是在分析中将不同的节点和自由度连接到一起的高级功能。当常规边界条件无法提供正确行为时，多点约束常用于仿真边界条件效应。

MPC 的用途之一是主从情况：节点 X（从属节点）处的位移需要与节点 Y（主节点）处的位移相同。在图 1 中，对长容器的一部分进行了建模。左侧使用对称边界条件，这将限制模型的 Z 平动并仿真左侧的储罐部分。对于长容器，模型右侧的储罐部分将强制这些节点保留在平面中。对称边界条件适用，但阻止储罐轴向增长或收缩的条件除外。此时，MPC 用于指示所有节点的 Z 位移都相等（但不一定是 0）。同样，MPC 可以热分析中的温度和静电分析中的电压为依据。

局部图：
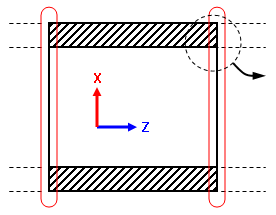
Z 对称条件限制左侧面。这些节点不会在 Z 方向上移动。   MPC 条件会将右侧面限制为保持在一个平面内，节点将在 Z 方向上一起移动。   如果没有 MPC 或其他边界条件，则载荷将导致右侧面上的节点自由变形。这样无法准确地仿真未包含在分析中的容器部分。
图 1：多点约束的使用
注： 在线性分析类型中，多点约束仅适用于“线性材料模型静态应力”和“固有频率(模态)”和“瞬态应力(直接积分)”。此外，使用模态结果（如响应谱、随机振动等）的线性分析类型会产生包括 MPC 效应的结果。对于热分析，MPC 可用于稳态和瞬态热传递。同样，静电分析的两种类型，即“电流和电压”和“场强度和电压”均支持 MPC。

多点约束的输入是使用以下格式的方程：

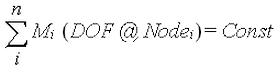
其中

如果方程涉及任何单位，则使用“模型单位”写入。MPC 方程不使用“显示单位”。

输入 MPC 方程

  1. 在“FEA 编辑器”中，写下 MPC 方程所需的顶点编号和关联的自由度。若要获取顶点编号，请使用“选择”“选择”“顶点”选择一个顶点，单击鼠标右键，然后选择“查询”。（或者，只需将鼠标指针悬停在顶点上，即会在工具提示中显示其属性。）
  2. 对于所有支持的分析类型，“多点约束”命令均位于功能区的“设置”选项卡中。
    • 对于线性结构分析，该命令位于“约束”面板的下拉部分中。
    • 对于热分析，该命令位于“热载荷”面板的下拉部分中。
    • 对于静电分析，该命令位于“载荷”面板的下拉部分中。
    此外，在未选择模型上的任何对象的情况下，可以在显示区域中单击鼠标右键，然后选择“添加”“多点约束”。使用“定义多点约束”对话框可输入上面的方程的所有项。
  3. 单击“添加”按钮以创建新的约束方程；系统将自动填充方程的名称。或者使用“方程名称”下拉菜单选择现有方程以进行编辑。
  4. 在“常数”字段中指定方程的常数。（上面的方程中的 Const。）
  5. 使用“添加行”按钮根据需要向电子表格添加多个行以指定方程中的各项。在每行中，输入“乘子”和“顶点 ID”（在步骤 2 中写下的顶点编号）以及相应的 DOF（自由度）。使用线性分析的可用下拉列表。对于热分析和静电分析，自由度是固定的（自由度分别为“温度”和“电压”）。
    注： 如果将顶点指定给局部坐标系，则选定的“自由度”也位于该局部坐标系中。例如，X 平动是指柱坐标系中的径向平动方向，Y 平动是指切向方向等。
  6. 选择“求解方法”并设置“罚函数乘子”（罚函数乘子用于“罚函数”方法）。可以从以下求解方法中选择：
    • 自动
    • 罚函数方法
    • 压缩方法
    注： 可以在相应的“设置”主题中找到建议的“罚函数”乘子值。搜索“罚函数乘子”可快速访问相关主题。
    注： 您在“定义多点约束”对话框中选择的求解方法将成为含 MPC 的所有特征将使用的方法。这些特征包括但不限于：循环对称、无摩擦约束、智能粘合和用户定义的 MPC。例如，如果要使用“罚函数方法”对涉及智能粘合的所有分析求解，则可在“定义多点约束”对话框中选择“罚函数方法”，以替代默认的压缩方法。
  7. 单击“确定”按钮关闭对话框。
  8. 运行分析。

兼容性说明：版本 20 到 20.4 SP1

不再兼容版本 20 到 20.4 SP1 中用于存储 MPC 数据的输入。若要恢复原始输入，请编辑位于设计工况文件夹（例如 modelname.ds_data\1）中的文件 DS.CST.BAK。这样可以得到原始 MPC 方程。节点编号需要转换为对应的顶点编号，然后需要通过“添加”“多点约束”重新输入方程。.CST.BAK 文件的格式如下所示：

#_equations, max_n 两个数：文件中的方程数 (#_equations) 和任意方程中的最大项数（max_n，不包括通过方程得出的常数）。两个数必须都是整数。
#_terms(1) 方程 1 中的项数。该数必须是整数。

node(1)、DOF(1)、M(1)

node(2)、DOF(2)、M(2)

node(3)、DOF(3)、M(3)

node(#_terms)、DOF(#_terms)、M(#_terms)

每行三个数，共有 #_terms 行。这三个数分别是节点编号 (node(i))，节点的自由度 (DOF(i)) 和项的乘子 (M(i))。乘子必须是实数，其他两个数必须是整数。DOF(i) 有效数字如下所示：

1 = X 平动
2 = Y 平动
3 = Z 平动
4 = X 转动
5 = Y 转动
6 = Z 转动
Constant(1) 方程 1 的常数值。此数必须是实数。（1.00 或 1.0E0，而不是 1）
  每个 MPC 方程（从数字 2 到 #_equations）都具有上面三行 [#_terms；node(i)、DOF(i)、M(i)；Constant]。

示例

分析图 2 中的齿轮系。请使用“多点约束”，而不是尝试使用梁单元对齿轮进行建模以模拟转动连接。对于齿轮，半径 1 * 转动 1 = - 半径 2 * 转动 2。因此 MPC 方程为“半径 1 * 转动 1 + 半径 2 * 转动 2 = 0”。对于给定的尺寸和顶点编号，MPC 的输入如下所示：

方程 1

常数 = 0

乘子 顶点 ID 自由度
3 12 X 转动
9 18 X 转动

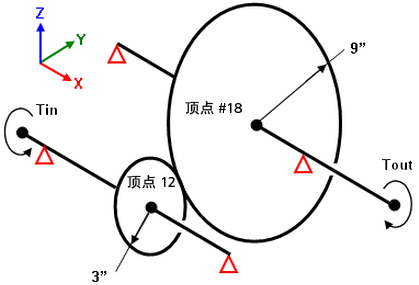
图 2：使用梁单元分析齿轮系

父主题： 载荷与约束